数学人教版14.3.2 公式法优秀课件ppt

这是一份数学人教版14.3.2 公式法优秀课件ppt，共31页。PPT课件主要包含了学习目标，自学指导一，1x2+y2，2x2–y2，3–x2–y2，4–x2+y2，5x3–25y2，6m2–m-1，x+yx–y，针对训练一等内容，欢迎下载使用。
1、探索并运用平方差公式因式分解.（A+B层）2、经历探索利用平方差公式进行因式分解的过程，感受逆向思维的意义，掌握因式分解的基本步骤.（A+B层）3.培养学生观察、分析和创新能力，深化学生的数学应用意识，渗透整体思想。（A层）
LEARNING OBJECTIVES
1.探索并运用平方差公式因式分解（重点）
2.经历探索利用平方差公式进行因式分解的过程，感受逆向思维的意义，掌握因式分解的基本步骤（难点）
自主学习，分析平方差公式因式分解的结构特征
独立思考，总结因式分解的一般步骤
课本116 思考-117练习上面，完成学案自主学习
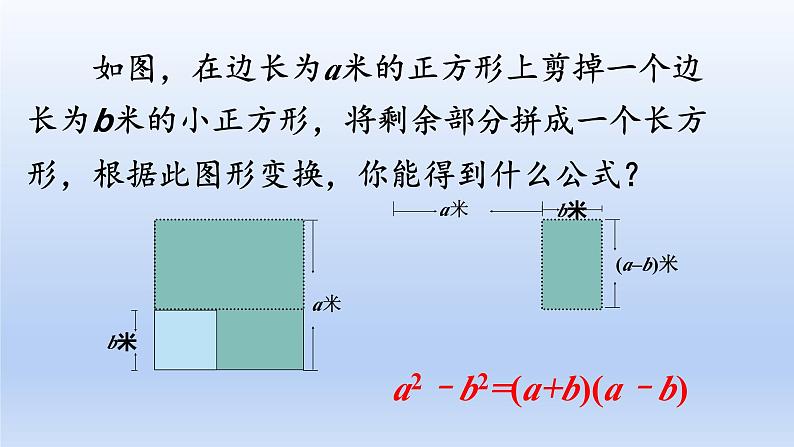
如图，在边长为a米的正方形上剪掉一个边长为b米的小正方形，将剩余部分拼成一个长方形，根据此图形变换，你能得到什么公式？
a2–b2=(a+b)(a–b)
多项式a2–b2有什么特点？你能将它分解因式吗？
是a，b两数的平方差的形式
两个数的平方差，等于这两个数的和与这两个数的差的乘积.
(a+b)(a-b)=a2-b2
a2-b2=(a+b)(a-b)
结构特征：左边 ：1.两项式 2.符号相反 3.均为平方形式即能写成: ( )2–( )2的形式.
右边：这两个数的和与这两个数的差的乘积.
辨一辨：下列多项式能否用平方差公式来分解因式，为什么？
y2–x2=(y+x)(y-x)
a2 – b2 =
分解因式：(1)(a＋b)2–4a2； A (2)9(m＋n)2–(m–n)2.
＝4(m＋2n)(2m＋n)．
＝(x2+y2)(x+y)(x–y);
(2)原式＝ab(a2–1)
＝ab(a+1)(a–1).
1.分解因式：(1)5m2a4–5m2b4； A
(2)a2–4b2–a–2b
2.在实数范围内分解因式：(1)m2–3； (2)x4-4.
例3 已知x2–y2＝–2，x＋y＝1，求x–y，x，y的值．
方法总结：在与x2–y2，x±y有关的求代数式或未知数的值的问题中，通常需先因式分解，然后整体代入或联立方程组求值.
已知x–y=2，x2–y2=8，求x+y的值.
解：由题意得：x2–y2=(x+y)(x–y)=8，∵x–y=2，∴ 2(x+y)=8，∴x+y=4.
例4 计算下列各题：(1)1012–992； (2)53.52×4-46.52×4.
方法总结：较为复杂的有理数运算，可以运用因式分解对其进行变形，使运算得以简化.
用平方差公式进行简便计算: (1)38²–37² (2)50×1252-50×252
例5 求证：当n为整数时，多项式(2n+1)2–(2n–1)2一定能被8整除．
方法总结：解决整除的基本思路就是将代数式化为整式乘积的形式，然后分析能被哪些数或式子整除．
(1)992–1能否被100整除？
(2)n为整数，(2n+1)2–25能否被4整除？
拓展提高(A层) 已知： ， ，求 的值；
拓展提高(A层)（1）已知： ， ，求 的值；（2）计算： ．
要求：独立完成， 书写规范， 10分钟后同桌交换，用红笔批阅
1.下列多项式中能用平方差公式分解因式的是(　　)A．a2＋(–b)2 B．5m2–20mnC．–x2–y2 D．–x2＋9
2. 将多项式x–x3因式分解正确的是(　　)A．x(x2–1) B．x(1–x2)C．x(x+1)(x–1) D．x(1+x)(1–x)
3.若a+b=3，a–b=7，则b2–a2的值为(　　)
A．–21 B．21 C．–10 D．10
4.把下列各式分解因式：(1)16a2–9b2=_________________; (2)(a+b)2–(a–b)2=_________________; (3) 因式分解：2x2–8=_________________; (4) –a4+16=_________________.
(4a+3b)(4a–3b)
(4+a2)(2+a)(2–a)
A 层5.若将(2x)n–81分解成(4x2+9)(2x+3)(2x–3)，则n的值是_______.
2(x+2)(x–2)
A 层6. 若a+b=4，a–b=1，则(a+1)2–(b–1)2的值为　 　．
解析：∵a+b=4，a–b=1，∴(a+1)2–(b–1)2=(a+1+b–1)(a+1–b+1)=(a+b)(a–b+2) =4×(1+2)=12．
A 层7.已知4m+n=40，2m–3n=5．求(m+2n)2–(3m–n)2的值．
8.如图，在边长为6.8 cm正方形钢板上，挖去4个边长为1.6 cm的小正方形，求剩余部分的面积．