中考数学一轮复习：专题13.11 全等三角形章末拔尖卷（华东师大版）（解析版）

这是一份中考数学一轮复习：专题13.11 全等三角形章末拔尖卷（华东师大版）（解析版），共33页。
参考答案与试题解析
选择题（共10小题，满分30分，每小题3分）
1．（3分）（2023春·四川绵阳·八年级四川省绵阳南山中学双语学校校考期中）如图，在△ABC中，∠BAC=120°，点D是BC上一点，BD的垂直平分线交AB于点E，将△ACD沿AD折叠，点C恰好与点E重合，则∠B等于（ ）
A．19°B．20°C．24°D．25°
【答案】B
【分析】根据垂直平分线和等腰三角形性质，得∠B=∠EDB；根据三角形外角性质，得∠AED=2∠B；根据轴对称的性质，得∠C=2∠B，∠EAD=60°，∠ADE=∠ADC；根据补角的性质计算得∠ADC=90°−∠B2，根据三角形内角和的性质列一元一次方程并求解，即可得到答案．
【详解】∵BD的垂直平分线交AB于点E，
∴EB=ED
∴∠B=∠EDB
∴∠AED=∠B+∠EDB=2∠B
∵将△ACD沿AD折叠，点C恰好与点E重合，
∴∠C=∠AED=2∠B，∠EAD=∠CAD=12∠BAC=60°，∠ADE=∠ADC
∵∠CDE=180°−∠EDB=180°−∠B
∴∠ADC=12∠CDE=90°−∠B2
∵∠CAD+∠ADC+∠C=180°
∴60+90°−∠B2+2∠B=180°
∴∠B=20°
故选：B．
【点睛】本题考查了轴对称、三角形内角和、三角形外角、补角、一元一次方程的知识；解题的关键是熟练掌握轴对称、三角形内角和、三角形外角的性质，从而完成求解．
2．（3分）（2023春·山东聊城·八年级校考期末）如图，线段AB，BC的垂直平分线l1，l2相交于点O．若∠OEB＝46°，则∠AOC＝（ ）
A．92°B．88°C．46°D．86°
【答案】B
【分析】根据线段垂直平分线的性质结合三角形外角性质得到∠AOC=2∠ABC，再利用垂直的定义结合直角三角形两锐角互余得到∠ABC=90°−∠OEB=90°−46°=44°，计算即可．
【详解】解：如图，连接BO并延长至点P，l1与线段AB交于F，
∵l1，l2是AB、BC的垂直平分线，
∴OA=OB，OB=OC，∠ODE=∠OFA=90°，
∴∠A=∠ABO，∠C=∠CBO
∴∠AOP=2∠ABO，∠COP=2∠CBO，
∴∠AOC=∠AOP+∠COP=2∠ABO+∠CBO=2∠ABC，
∵∠OEB＝46°，∠OFA=90°，
∴∠ABC=90°−∠OEB=90°−46°=44°，
∴∠AOC=2∠ABC=2×44°=88°，
故选：B
【点睛】本题考查了线段垂直平分线的性质，三角形外角的性质，垂直的定义，直角三角形两锐角互余，注意掌握辅助线的作法，注意掌握整体思想与数形结合思想的应用．
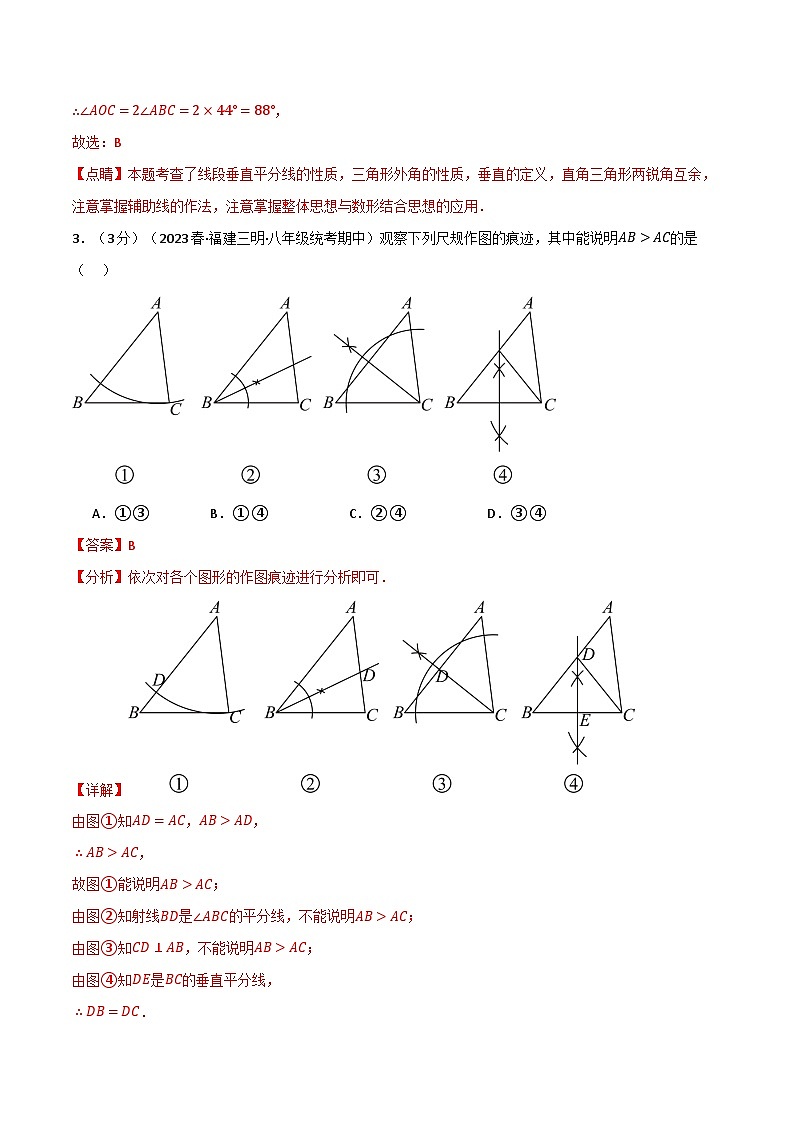
3．（3分）（2023春·福建三明·八年级统考期中）观察下列尺规作图的痕迹，其中能说明AB>AC的是（ ）

A．①③B．①④C．②④D．③④
【答案】B
【分析】依次对各个图形的作图痕迹进行分析即可．
【详解】
由图①知AD=AC，AB>AD，
∴AB>AC，
故图①能说明AB>AC；
由图②知射线BD是∠ABC的平分线，不能说明AB>AC；
由图③知CD⊥AB，不能说明AB>AC；
由图④知DE是BC的垂直平分线，
∴DB=DC．
∵△ADC中AD+DC>AC，
∴AD+DB>AC，
即AB>AC．
故图④能说明AB>AC．
故选：B
【点睛】本题主要考查了尺规作图法，和三角形三边之间的关系．初中阶段常考的尺规作图有：做一条线段等于已知线段，做一个角的平分线，过直线外一点作已知直线的垂线，做一条线段的垂直平分线．熟练掌握以上尺规作图的方法，并且懂得其中的原理是解题的关键．
4．（3分）（2023春·山东济宁·八年级校考期末）如图，将ΔABC沿DE、EF翻折，使其顶点A、B均落在点O处，若∠CDO+∠CFO=72∘，则∠C的度数为（ ）
A．36∘B．54∘C．64∘D．72∘
【答案】B
【分析】由折叠的性质可得∠A=∠DOE，∠B=∠EOF，可得∠DOF=∠A+∠B，由三角形内角和定理可得∠A+∠B=180°−∠C，利用三角形外角定理得出∠DOF=∠C+∠CDO+∠CFO，建立方程，即可求∠C的度数．
【详解】解：延长FO交AC于点M，
∵将ΔABC沿DE，EF翻折，顶点A，B均落在点O处，
∴∠A=∠DOE，∠B=∠EOF，
∴∠DOF=∠A+∠B，
∵∠A+∠B+∠C=180°，
∴∠A+∠B=180°−∠C ，
由三角形外角定理可知：∠DOF=∠MDO+∠DMO，∠DMO=∠C+∠CFM，
∴∠DOF=∠C+∠CDO+∠CFO
即：∠DOF=∠C+∠CDO+∠CFO=180°−∠C，
∴∠C+72°=180°−∠C ，
∴∠C=54°，
故选：B．
【点睛】本题考查了折叠的性质，三角形内角和定理，外角定理，熟练运用三角形内角和定理是本题的关键．
5．（3分）（2023春·陕西榆林·八年级校考期中）如图，E为AC上一点，连接BE，CD平分∠ACB交BE于点D，且BE⊥CD，∠A=∠ABE，AC=8，BC=5，则BD的长为（ ）
A．1.2B．1.5C．2D．3
【答案】B
【分析】由CD平分∠ACB，BE⊥CD可得CE=BC=5，BD=DE，再由等腰三角形的判定和性质可得BE=AE，代入数值进行计算即可得到答案．
【详解】解：∵ CD平分∠ACB，BE⊥CD，
∴CE=BC=5，BD=DE，
∴AE=AC−CE=8−5=3，
∵ ∠A=∠ABE，
∴BE=AE=3，
∴BD=DE=12BE=1.5，
故选：B．
【点睛】本题考查了等腰三角形的判定与性质，注意等腰三角形“三线合一”性质的运用．
6．（3分）（2023春·河南周口·八年级统考期末）如图，直线a，b相交于点O，∠1=50°，点A在直线a上，直线b上存在点B，使以点O，A，B为顶点的三角形是等腰三角形，则点B的个数是（ ）
A．2B．3C．4D．5
【答案】C
【分析】分AO=AB，BO=BA，OB=OA三种情况讨论．
【详解】∵直线a，b相交于点O，∠1=50°，点A在直线a上，直线b上存在点B，
∴当OB=OA时，有两个B点是B1、B2，OB1=OA时，∠OB1A=∠OAB1= 12∠1=25°，OB2=OA时，∠OB2A=∠OAB2= 12（180°-∠1）=65°；
当AO=AB时，有一个B点是B3，即AO=AB3，∠AB3O=∠1=50°；
当BO=BA时，有一个B点是B4，即B4O=B4A,∠OAB4=∠1=50°．
∴使以点O，A，B为顶点的三角形是等腰三角形，点B的个数是4个．
故选C．
【点睛】本题考查了因动点产生的等腰三角形问题，解决问题的关键是三角形的三边两两相等都有可能，有三种可能情况，分类讨论．
7．（3分）（2023春·浙江台州·八年级台州市书生中学校考期中）如图，△ABC中，AB＝AC，∠BAC＝90°，点D在线段BC上，∠EDB＝12∠ACB，BE⊥DE，DE与AB相交于点F，若BE＝4，则DF＝（ ）
A．6B．8C．10D．12
【答案】B
【分析】过点D作AC的平行线交BE的延长线于H，交AB于G，则可得DB=DH，从而BH=2BE，又可证明△HGB≌△FGD， 则DF=BH，从而可求得DF的长．
【详解】过点D作AC的平行线交BE的延长线于H，交AB于G，如图所示
∵DH∥AC
∴∠BDH=∠ACB
∵∠EDB＝12∠ACB
∴∠EDB＝12∠BDH
∴∠EDB=∠EDH
∵BE⊥DE
∴∠DEB=∠DEH
∴∠DBE=∠DHE
∴DB=DH
即△DBH是等腰三角形
∴BH=2BE=2×4=8
∵AB=AC，∠BAC=90°
∴∠ACB=∠ABC=45°
∴∠EDB=∠EDH=12∠ACB=22.5°
∵BE⊥DE
∴∠EBD=90°-∠EDB=67.5°
∴∠HBG=∠EBD-∠ABC=22.5°
∴∠HBG=∠EDH
∵∠BDH=∠ACB=∠ABC=45°
∴GB=GD，∠BGD=90°
在Rt△HGB和Rt△FGD中
∠BGH=∠DGF=90°BG=DG∠HBG=∠EDH
∴△HGB≌△FGD
∴DF=BH=8
故选：B．
【点睛】本题主要考查了等腰三角形的判定与性质，全等三角形的判定与性质，构造辅助线得到全等三角形是问题的关键．
8．（3分）（2023春·河南周口·八年级校考期末）如图，在△ABC中，AB=AC，D为BC上的一点，∠BAD=28°，在AD的右侧作△ADE，使得AE=AD，∠DAE=∠BAC，连接CE、DE，DE交AC于点O，若CE∥AB，则∠DOC的度数为（ ）

A．124°B．102°C．92°D．88°
【答案】C
【分析】先证明△ABD≌△ACE得到∠B=∠ACE，∠CAE=∠BAD=28°，由等腰三角形的性质可得∠B=∠ACB，从而得到∠B=∠ACB=∠ACE，再由平行线的性质可得∠B+∠ACB+∠ACE=180°，从而得到∠B=∠ACB=∠ACE=60°，再由等边三角形的判定和性质可得∠ADE=60°，∠DAC=∠DAE−∠CAE=32°，再由三角形外角的定义和性质进行计算即可得到答案．
【详解】解：∵∠DAE=∠BAC，
∴∠BAC−∠DAC=∠DAE−∠DAC，
∴∠BAD=∠CAE，
在△ABD和△ACE中，
AB=AC∠BAD=∠CAEAD=AE，
∴△ABD≌△ACESAS，
∴∠B=∠ACE，∠CAE=∠BAD=28°，
∵AB=AC，
∴∠B=∠ACB，
∴∠B=∠ACB=∠ACE，
∵CE∥AB，
∴∠B+∠BCE=180°，即∠B+∠ACB+∠ACE=180°，
∴∠B=∠ACB=∠ACE=60°，
∵AB=AC，
∴△ABC是等边三角形，
∴∠BAC=∠DAE=60°，
∵AD=AE，
∴△ADE是等边三角形，
∴∠ADE=60°，
∵∠DAC=∠DAE−∠CAE=60°−28°=32°，
∴∠DOC=∠ADO+∠DAO=60°+32°=92°，
故选：C．
【点睛】本题考查了全等三角形的判定与性质、等边三角形的判定与性质、等腰三角形的性质、三角形外角的定义与性质、平行线的性质，熟练掌握以上知识点是解题的关键．
9．（3分）（2023春·全国·八年级专题练习）如图，在△ABC中，∠A=60°，∠ABC和∠ACB的平分线BD、CE相交于点O，BD交AC于点D，CE交AB于点E，若已知△ABC周长为20，BC=7，AE:AD=4:3，则AE长为（ ）
A．187B．247C．267D．4
【答案】B
【分析】证明△BOE≌△BOH得出∠EOH=∠BOH=60°，证明△COD≌△COH得出CD=CH，进而即可求解．
【详解】解：如图，在BC上截取BH=BE，连接OH
∵BD平分∠ABC，CE平分∠ACB，
∴∠ABD=∠CDB,∠ACE=∠BCE，
∵∠A=60°，
∴∠ABC+∠ACB=120°，
∴∠DBC+∠BCE=60°，
∴∠BOC=120°，
∴∠BOE=∠COD=60°，
在△BOE和△BOH中，
BE=BH∠ABD=∠CBDBO=BO，
∴△BOE≌△BOH(SAS)，
∴∠EOB=∠BOH=60°，
∴∠COH=∠BOC−∠BOH=60°，
∴ ∠COD=∠COH=60°，
在△COD和△COH中，
∠ACE=∠BCEOC=OC∠COD=∠COH，
∴△COD≌△COH(ASA)，
∴CD=CH，
∴BE+CD=BH+CH=BC=7，
∵ △ABC周长为20，
∴AB+AC+BC=20，
∴AE+AD=6，
∵AE:AD=4:3，
∴AE=67×4=247．
故选：B．
【点睛】本题考查了全等三角形的性质与判定，角分线的定义，构造全等三角形是解题的关键．
10．（3分）（2023春·山东枣庄·八年级校考期中）如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正△ABC和正△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ，以下五个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°．一定成立的结论有（ ）．

A．①②③B．①②④C．①②③④D．①②③⑤
【答案】D
【分析】①由于△ABC和△CDE是等边三角形，可知AC=BC，CD=CE，∠ACB=∠DCE=60°，从而证出△ACD≌△BCE，可推知AD=BE；②由△ACD≌△BCE得∠CBE=∠DAC，加之∠ACB=∠DCE=60°，AC=BC，得到△CQB≌△CPAASA，再根据∠PCQ=60°推出△PCQ为等边三角形，又由∠PQC=∠DCE，根据内错角相等，两直线平行，可知②正确；③同②得：△ACP≌△BCQ，即可得出结论；④根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ，∠CDE=60°，可知∠DQE≠∠CDE，可知④错误；⑤利用等边三角形的性质，BC∥DE，再根据平行线的性质得到∠CBE=∠DEO，于是可知⑤正确．
【详解】解：①∵△ABC和△CDE是等边三角形，
∴AC=BC，CD=CE，∠ACB=∠DCE=60°，
∴∠ACD=∠BCE，
在△ACD和△BCE中，
AC=BC∠ACD=∠BCECD=CE
∴△ACD≌△BCESAS，
∴AD=BE，∠ADC=∠BEC，①正确；
②∠DCP=180°−2×60°=60°=∠ECQ，
在△CDP和△CEQ中，
∠ADC=∠BEC∠DCP=∠ECQCD=CE
∴△CDP≌△CEQASA，
∴CP=CQ，
∴∠CPQ=∠CQP=60°，
∴∠QPC=∠BCA，
∴PQ∥AE，②正确；
③与②的过程同理得：△ACP≌△BCQ，
∴AP=BQ，
③正确；
④∵DE＞QE，且DP=QE，
∴DE＞DP，故④错误；
⑤∵∠ACB=∠DCE=60°，
∴∠BCD=60°，
∵△DCE是等边三角形，∠EDC=60°=∠BCD，
∴BC∥DE，
∴∠CBE=∠DEO，
∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°，
∴⑤正确．
故选：D
【点睛】本题考查了等边三角形的性质、全等三角形的判定与性质；熟练掌握等边三角形的性质，证明三角形全等是解决问题的关键．
二．填空题（共6小题，满分18分，每小题3分）
11．（3分）（2023春·山东青岛·八年级统考期末）如图，在△ABC中，∠A=52°，∠ACB的角平分线CF与BC的垂直平分线DE交于点O，连接OB．若∠ABO=20°，则∠ACB= ．

【答案】72°/72度
【分析】由线段垂直平分线的性质可得∠OBC=∠OCB，由角平分线的定义可得∠ACF=∠OCB，再利用三角形的内角和定理可求得∠ACF的度数，进而可求解．
【详解】解：∵OE垂直平分BC，
∴OB=OC，
∴∠OBC=∠OCB，
∵CF平分∠ACB，
∴∠ACF=∠OCB，
∵∠A+∠ABC+∠ACB=180°，
∴∠A+∠ABO+3∠ACF=180°，
∵∠A=52°，∠ABO=20°，
∴∠ACF=36°，
∴∠ACB=2∠ACF=72°．
故答案为：72°．
【点睛】本题主要考查线段垂直平分线的性质，角平分线的定义，三角形的内角和定理，利用三角形的内角和定理求解∠ACF的度数是解题的关键．
12．（3分）（2023春·重庆巫溪·八年级统考期末）如图，在△ABC中，点D，点E分别在边AC，BC上，AB=AE=AD，DE=DC，若∠C=42°，则∠BAE的度数为 度．
【答案】72
【分析】根据等腰三角形的性质得出∠DEC=42°，进而利用三角形内角和定理解答即可．
【详解】解：∵∠C=42°，DE=DC，
∴∠DEC=42°，
∴∠ADE=42°+42°=84°，
∵AE=AD，
∴∠AED=84°，
∴∠AEC=84°+42°=126°，
∴∠AEB=180°−126°=54°，
∵AB=AE，
∴∠BAE=180°−54°−54°=72°，
故答案为：72．
【点睛】此题考查了等腰三角形的性质，解题的关键是根据等腰三角形的性质得出∠DEC=42°解答．
13．（3分）（2023春·浙江宁波·八年级校考期末）如图，在△ABC中，BD为AC边上的中线，F为AB上一点，连接CF交BD于点E，若AB=CE=4，5AF=4AB，则EF=______．

【答案】45
【分析】过A点作AG∥CF交BD的延长线于点G，证明利用AAS证明△ADG≌△CDE可得AG=CE，结合等腰三角形的性质可证∠ABG=∠G=∠BEF，进而可得BF=EF，再根据AB=CE=4，5AF=4AB，可求出BF的长，即可求解．
【详解】解：过A点作AG∥CF交BD的延长线于点G，

∴∠G=∠DEC，
∵BD是AC边上的中线，
∴AD=CD，
在△ADG和△CDE中，
∠G=∠DEC∠ADG=∠CDEAD＝CD，
∴△ADG≌△CDEAAS，
∴AG=CE，
∵CE=AB=4，
∴∠ABG=∠G，
∴∠ABG=∠DEC=∠BEF，
∴BF=EF，
∵AB=CE=4，5AF=4AB，
∴AF=3.2，
∴BF=AB−AF=45，
∴EF=45．
故答案为：45．
【点睛】本题主要考查等腰三角形的性质与判定，全等三角形的判定与性质，构造全等三角形是解题的关键．
14．（3分）（2023春·四川成都·八年级统考期末）如图，在直角三角形ABC中，∠C=90°，点D在AB上，点G在BC上，△BDG与△FDG关于直线DG对称，DF与B交于点E，若DF∥AC，∠B=28°，则∠DGC的度数是 度．
【答案】59
【分析】由轴对称的性质可得∠F=∠B=28°，∠DGB=∠DGF，利用平行线的性质和对称性质求出∠EGF=62°，∠DGC=x°，则∠DGB=∠DGF=62°+x°，再由∠DGC+∠DGB=180°，可得x+62+x=180，解方程即可得到答案．
【详解】解：由轴对称的性质可得∠F=∠B=28°，∠DGB=∠DGF，
∵DF∥AC，∠C=90°，
∴∠DEB=∠C=90°，
∴∠EGF=∠DEB−∠F=62°，
设∠DGC=x°，则∠DGB=∠DGF=∠DGC+∠EGF=62°+x°，
∵∠DGC+∠DGB=180°，
∴x+62+x=180，
∴x=59，
∴∠DGC=59°，
故答案为：59．
【点睛】本题主要考查了轴对称的性质，正确求出∠EGF=62°是解题的关键．
15．（3分）（2023春·四川成都·八年级期中）已知：△ABC是三边都不相等的三角形，点P是三个内角平分线的交点，点O是三边垂直平分线的交点，当P、O同时在不等边△ABC的内部时，那么∠BOC和∠BPC的数量关系是 ．
【答案】∠BOC=4∠BPC−360°
【分析】根据三角形角平分线的性质以及三角形内角和定理，即可得到∠BAC=2∠BPC−180°；再根据三角形垂直平分线的性质以及三角形内角和定理，即可得到∠BOC=2∠BAC，进而得出∠BOC和∠BPC的数量关系．
【详解】解：∵BP平分∠ABC，CP平分∠ACB，
∴∠PBC=12∠ABC，∠PCB=12∠ACB，
∴∠BPC=180°−(∠PBC+∠PCB)
=180°−( 12∠ABC+12∠ACB)
=180°−12(∠ABC+∠ACB)
=180°−12(180°−∠BAC)
=90°+12∠BAC，
即∠BAC=2∠BPC−180°；
如图，连接AO．
∵点O是这个三角形三边垂直平分线的交点，
∴OA=OB=OC，
∴∠OAB=∠OBA，∠OAC=∠OCA，∠OBC=∠OCB，
∴∠AOB=180°−2∠OAB，∠AOC=180°−2∠OAC，
∴∠BOC=360°−(∠AOB+∠AOC)
=360°−(180°−2∠OAB+180°−2∠OAC)，
=2∠OAB+2∠OAC
=2∠BAC
=2(2∠BPC−180°)
=4∠BPC−360°，
故答案为：∠BOC=4∠BPC−360°．
【点睛】本题考查了三角形的垂直平分线与角平分线，熟练掌握三角形的垂直平分线与角平分线的性质是解题的关键．
16．（3分）（2023春·浙江台州·八年级统考期末）如图，以△ABC∠ABC>120°三边为边向外作等边三角形，分别记△ABC，△ABD，△BCE，△ACF面积为S，S1，S2，S3，作△ABD关于AB对称的△ABM，连接MF，BF．若△ABC≌△BMF，则∠ABC= ，S3= （用含S，S1，S2的式子表示）．
【答案】 150°； 3S+S1+S2．
【分析】根据△ABD，△ACF，△ABM为等边三角形，证明△AMF≌△BMF，从而求出∠ABC的度数；把△ABC绕点C顺时针旋转60度，AC边落在FC得到△FNC，连接NB，证明△FNC≌△ABC，△NCB≌△BCE，△FNB≌△FNC，从而求出S3．
【详解】∵△ABC≌△BMF
∴AC=BF，∠ABC=∠BMF
∵由题意知：△ABD，△ACF，△ABM为等边三角形，
∴BF=AF=AC，AM=BM=AB
∵MF=MF
∴△AMF≌△BMF
∴∠ABC=∠AMF=∠BMF=360°−60°2=150°
把△ABC绕点C顺时针旋转60度，AC边落在FC得到△FNC，连接NB，
则△FNC≌△ABC，
∴NC=BC，∠FCN=∠ACB
∴∠NCB=∠FCA=∠NCA+∠FCN=60°
∴△NCB为等边三角形且△NCB≌△BCE
∵NC=BC，FB=FC，FN=FN
∴△FNB≌△FNC
综上所述：S△FMB=S△FNB=S△FNC=S△ABC=S，
S△AMB=S△ABD=S1，S△NBC=S△BCE=S2
∴S3=3S+S1+S2
【点睛】本题考查全等三角形的性质与判定，等边三角形的性质与判定，解题的关键是能够证明三角形全等，进而求出面积的关系．
三．解答题（共7小题，满分52分）
17．（6分）（2023春·河北邯郸·八年级校考期中）如图，△ABC和△DEC都是等边三角形，连接AD、BE，延长E交AD于F点．
(1)证明：△BEC≌△ADC．
(2)如果△DEC绕点C转动，并且0°