
还剩7页未读,
继续阅读
成套系列资料,整套一键下载
2024八年级数学下册第十九章一次函数综合素质评价试卷(人教版附答案)
展开
这是一份2024八年级数学下册第十九章一次函数综合素质评价试卷(人教版附答案),共10页。
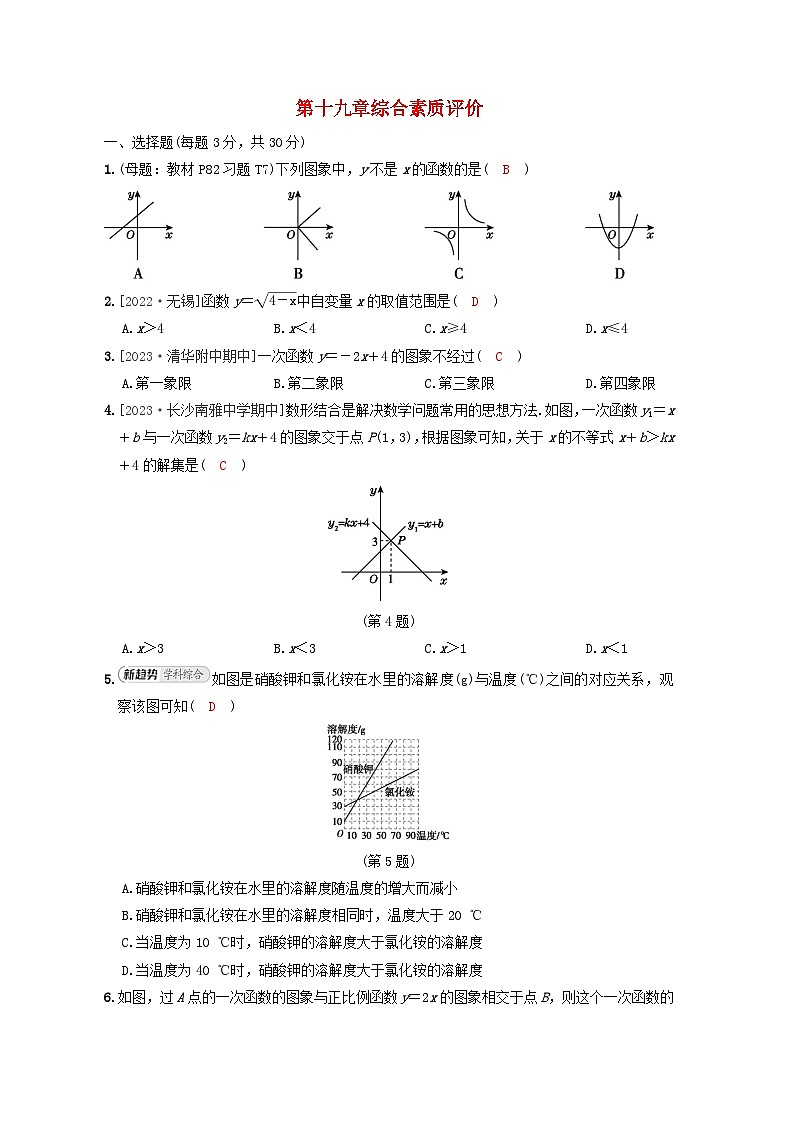
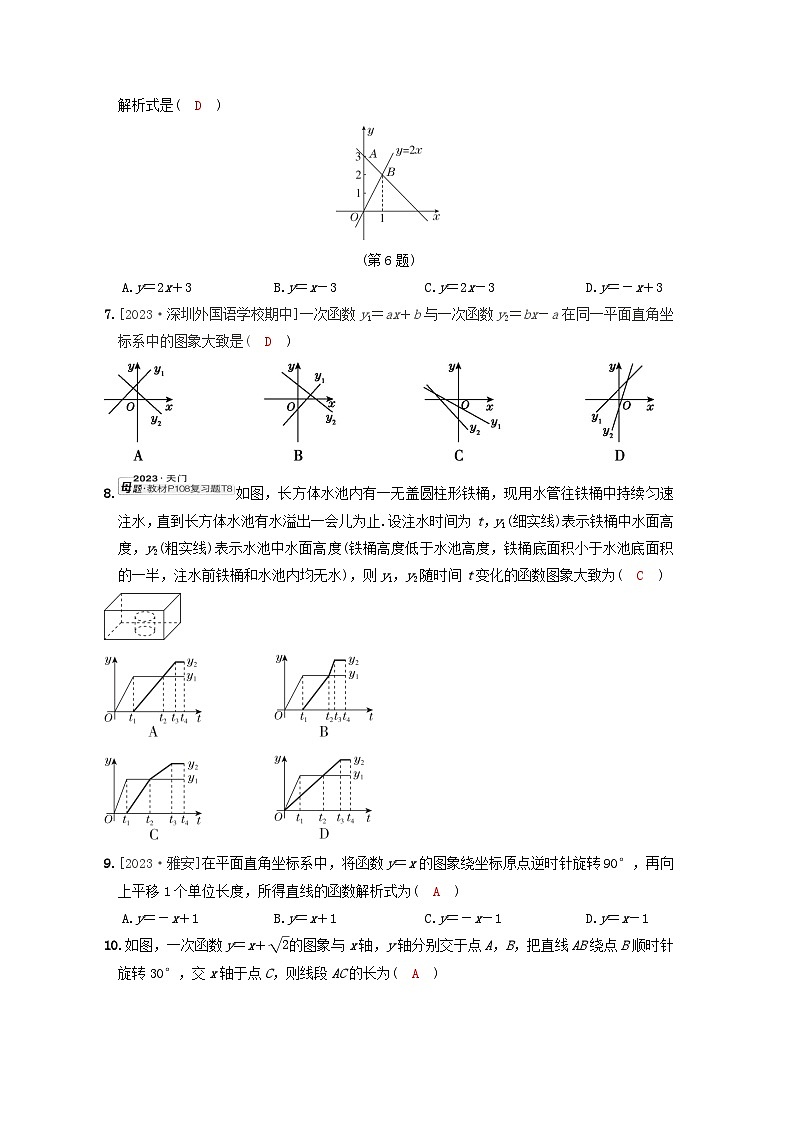
第十九章综合素质评价一、选择题(每题3分,共30分)1.(母题:教材P82习题T7)下列图象中,y不是x的函数的是( B )2.[2022·无锡]函数y=4-x中自变量x的取值范围是( D )A.x>4 B.x<4 C.x≥4 D.x≤43.[2023·清华附中期中]一次函数y=-2x+4的图象不经过( C )A.第一象限 B.第二象限 C.第三象限 D.第四象限4.[2023·长沙南雅中学期中]数形结合是解决数学问题常用的思想方法.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),根据图象可知,关于x的不等式x+b>kx+4的解集是( C )(第4题)A.x>3 B.x<3 C.x>1 D.x<15.如图是硝酸钾和氯化铵在水里的溶解度(g)与温度(℃)之间的对应关系,观察该图可知( D )(第5题)A.硝酸钾和氯化铵在水里的溶解度随温度的增大而减小B.硝酸钾和氯化铵在水里的溶解度相同时,温度大于20 ℃C.当温度为10 ℃时,硝酸钾的溶解度大于氯化铵的溶解度D.当温度为40 ℃时,硝酸钾的溶解度大于氯化铵的溶解度6.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( D )(第6题)A.y=2x+3 B.y=x-3 C.y=2x-3 D.y=-x+37.[2023·深圳外国语学校期中]一次函数y1=ax+b与一次函数y2=bx-a在同一平面直角坐标系中的图象大致是( D )8.如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为t,y1(细实线)表示铁桶中水面高度,y2(粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则y1,y2随时间t变化的函数图象大致为( C ) 9.[2023·雅安]在平面直角坐标系中,将函数y=x的图象绕坐标原点逆时针旋转90°,再向上平移1个单位长度,所得直线的函数解析式为( A )A.y=-x+1 B.y=x+1 C.y=-x-1 D.y=x-110.如图,一次函数y=x+2的图象与x轴,y轴分别交于点A,B,把直线AB绕点B顺时针旋转30°,交x轴于点C,则线段AC的长为( A )(第10题)A.6+2 B.32 C.2+3 D.3+2二、填空题(每题3分,共24分)11.请写出一个函数的解析式,使得它的图象经过点(2,0): y=x-2(答案不唯一) .12.(母题:教材P107复习题T2)一次函数y=x-2的图象与y轴的交点坐标是 (0,-2) .13.若点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,则y1-y2 > 0.(填“>”或“<”)14.[2023·成都外国语学校月考]如图,函数y=ax和y=kx+b的图象相交于点A,则关于x,y的方程组y=kx+b,y=ax的解为 x=-2,y=1 .(第14题)15.若直线y=2x+b与坐标轴围成的三角形的面积为6,则b= ±26 .16.若关于x的一元一次不等式组23x>x-1,4x+1≥a恰有3个整数解,且一次函数y=(a-2)x+a+1的图象不经过第三象限,则a的取值范围是 -1≤a≤1 .17.[2022·辽宁]如图,直线y=2x+4与x轴交于点A,与y轴交于点B,点D为OB的中点,▱OCDE的顶点C在x轴上,顶点E在直线AB上,则▱OCDE的面积为 2 .(第17题)18.为落实“双减”政策,某校利用课后服务时间举行趣味运动会,在直线跑道上,甲同学从A处匀速跑向B处,乙同学从B处匀速跑向A处,两人同时出发,到达各自终点后立即停止运动,设甲同学跑步的时间为x(s),甲、乙两人之间的距离为y(m),y与x之间的函数关系如图所示,则图中t的值是 403 .(第18题)三、解答题(19题8分,20,21题每题10分,22,23题每题12分,24题14分,共66分)19.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),求此一次函数的解析式.【解】设一次函数的解析式为y=kx+b(k≠0).∵一次函数的图象与直线y=-x+1平行,∴k=-1.∴一次函数的解析式为y=-x+b.∵一次函数的图象经过点(8,2),∴2=-8+b,解得b=10.∴一次函数的解析式为y=-x+10.20.(母题:教材P108复习题T9)把一个长10 cm,宽5 cm的长方形的长减少x cm,宽不变,得到的长方形的面积为y cm2.(1)请写出y与x之间的函数关系式;(2)请写出自变量x的取值范围;(3)画出函数的图象.【解】(1)根据题意得y=5(10-x),整理,得y=-5x+50.(2)0≤x<10.(3)如图所示.21.[2023·北师大实验中学期中]在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象由函数y=-x的图象平移得到,且经过点(1,1).(1)求这个一次函数的解析式;(2)当x<1时,对于x的每一个值,函数y=mx-1(m≠0)的值小于一次函数y=kx+b的值,直接写出m的取值范围.【解】(1)∵一次函数y=kx+b(k≠0)的图象由函数y=-x的图象平移得到,∴k=-1.将点(1,1)的坐标代入y=-x+b,解得b=2,∴一次函数的解析式是y=-x+2.(2)-1≤m≤2且m≠0.22.某加油站推出促销活动,一张加油卡的面值是1 000元,打九折出售,使用这张加油卡加油,油的单价降低0.30元/L.假设这张加油卡的面值能够一次性全部用完.(1)购买这张加油卡实际要付多少钱?(2)用这张加油卡加油后油的单价为y元/L,原价为x元/L,求y关于x的函数解析式(不用写出自变量的取值范围).(3)油的原价是7.30元/L,求用这张加油卡加油后油的单价比原价便宜多少?【解】(1)1 000×0.9=900(元),答:购买这张加油卡实际要付900元.(2)由题意知,y=0.9(x-0.30),整理得y=0.9x-0.27,∴y关于x的函数解析式为y=0.9x-0.27.(3)当x=7.30时,y=0.9×7.30-0.27=6.30,∵7.30-6.30=1.00(元/L),∴使用这张加油卡加油后油的单价比原价便宜1.00元/L.23.[2022·河北]如图,在平面直角坐标系中,线段AB的端点为A(-8,19),B(6,5).(1)求AB所在直线的解析式;(2)某同学设计了一个动画:在函数y=mx+n(m≠0,y≥0)中,分别输入m和n的值,便得到射线CD,其中C(c,0),当c=2时,会从C处弹出一个光点P,并沿CD飞行;当c≠2时,只发出射线而无光点弹出.①若有光点P弹出,试推算m,n应满足的数量关系;②当有光点P弹出,并击中线段AB上的整点(横、纵坐标都是整数)时,线段AB就会发光,求此时整数m的个数.【解】(1)设直线AB的解析式为y=kx+b(k≠0).把点A(-8,19),B(6,5)的坐标分别代入y=kx+b,得-8k+b=19,6k+b=5,解得k=-1,b=11.∴AB所在直线的解析式为y=-x+11.(2)①由题意知,直线y=mx+n经过点C(2,0),∴2m+n=0.②设线段AB上的整点为(t,-t+11),则tm+n=-t+11,∵2m+n=0,∴(t-2)m=-t+11.易知t-2≠0.∴m=-t+11t-2=-1+9t-2.∵t为整数,m也是整数,∴t-2=±1或±3或±9.解得t=1,3,5,-1,-7或11.∵-8≤t≤6,∴t=11不符合题意,舍去.当t=1时,m=-10;当t=3时,m=8;当t=5时,m=2;当t=-1时,m=-4;当t=-7时,m=-2.∴符合题意的整数m的个数为5.24.某动力科学研究院实验基地内装有一段笔直的轨道AB,长度为1m的金属滑块在上面做往返滑动.如图,滑块首先沿AB方向从左向右匀速滑动,滑动速度为9 m/s,滑动开始前滑块左端与点A重合,当滑块右端到达点B时,滑块停顿2 s,然后再以小于9 m/s的速度匀速返回,直到滑块的左端与点A重合,滑动停止.设滑块滑动的时间为t(s)时,滑块左端离点A的距离为l1(m),右端离点B的距离为l2(m),记d=l1-l2,d与t具有函数关系,已知滑块在从左向右滑动过程中,当t=4.5和5.5时,与之对应的d的两个值互为相反数;滑块从点A出发到最后返回点A,整个过程总用时27 s(含停顿时间).请你根据所给条件解决下列问题:(1)滑块从点A到点B的滑动过程中,d的值 由负到正 ;(填“由负到正”或“由正到负”)(2)滑块从点B到点A的滑动过程中,求d与t的函数解析式;(3)在整个往返过程中,若d=18,求t的值.【解】(2)设轨道AB的长为n m,当滑块从左向右滑动时,∵l1+l2+1=n,∴l2=n-l1-1.∴d=l1-l2=l1-(n-l1-1)=2l1-n+1=2×9t-n+1=18t-n+1.∴d是t的一次函数.∵当t=4.5和5.5时,与之对应的d的两个值互为相反数,∴当t=5时,d=0.∴18×5-n+1=0.∴n=91.∴滑块从点A到点B所用的时间为(91-1)÷9=10(s).∵整个过程总用时27 s(含停顿时间),且当滑块右端到达点B时,滑块停顿2 s,∴滑块从B返回到A所用的时间为27-10-2=15(s).∴滑块返回的速度为(91-1)÷15=6(m/s),∴当12≤t≤27时,l2=6(t-12).此时l1=91-1-l2=90-6(t-12)=162-6t.∴d=l1-l2=162-6t-6(t-12)=-12t+234.∴滑块从点B到点A的滑动过程中,d与t的函数解析式为d=-12t+234.(3)当d=18时,有两种情况:①当0≤t≤10时,18t-90=18,解得t=6.②当12≤t≤27时,-12t+234=18,解得t=18.综上所述,当t为6或18时,d=18. 第十九章综合素质评价一、1.B 【点拨】自变量x在取值范围内任取一个值,因变量y有唯一确定的值与之对应,则y是x的函数,A,C,D均满足任取一个x的值,有唯一确定的y值和它对应,则y是x的函数,而B中,x取一个正数,与之对应的有两个y值,故y不是x的函数,故选B.2.D 3.C 4.C 5.D 6.D7.D 【点拨】根据函数图象,确定a,b的正负,看看是否矛盾即可.8.C9.A 【点拨】在函数y=x的图象上取点A(1,1),绕原点逆时针方向旋转90°后得到对应的点的坐标为A'(-1,1),则旋转后的直线的解析式为y=-x.再向上平移1个单位长度,得到的直线的解析式为y=-x+1.10.A 【点拨】在一次函数y=x+2中,令x=0,则y=2;令y=0,则x=-2.∴A(-2,0),B(0,2).∴OA=OB=2.∴△OAB为等腰直角三角形,∠OAB=45°.∴AB=(2)2+(2)2=2.如图,过点C作CD⊥AB,垂足为点D.∵∠CAD=∠OAB=45°,∴△ACD为等腰直角三角形.设CD=AD=a,∴AC=AD2+CD2=2a.∵直线AB绕点B顺时针旋转30°得到直线CB,∴∠ABC=30°.∴BC=2CD=2a.∴BD=BC2-CD2=3a.又∵BD=AB+AD=2+a.∴2+a=3a,解得a=3+1.∴AC=2a=2(3+1)=6+2.二、11.y=x-2(答案不唯一)12.(0,-2)【点拨】根据一次函数的图象与y轴的交点的横坐标等于0,将x=0代入y=x-2,可得y的值,从而可以得到一次函数y=x-2的图象与y轴的交点坐标.13.>14.x=-2,y=1【点拨】根据图象可知,函数y=ax和y=kx+b的图象的交点A的坐标是(-2,1),所以关于x,y的方程组y=kx+b,y=ax的解为x=-2,y=1.15.±26 【点拨】已知直线与两坐标轴所围成的三角形的面积,求直线对应的函数解析式的方法:先设出直线对应的函数解析式,再用待定字母表示出直线与两坐标轴的交点坐标(注:这步中要考虑直线与x轴,y轴相交时的位置的不同情况),然后利用已知三角形的面积求出待定字母的值,最后代回所设函数解析式即可.16.-1≤a≤1 17.218.403【点拨】由图象和题意可知,乙在t s时到达A处,甲在20 s时到达B处,则V甲=8020=4(m/s),第8 s时两人相遇,则(V乙+4)×8=80.解得V乙=6 m/s,则6t=80,解得t=403.三、19.【解】设一次函数的解析式为y=kx+b(k≠0).∵一次函数的图象与直线y=-x+1平行,∴k=-1.∴一次函数的解析式为y=-x+b.∵一次函数的图象经过点(8,2),∴2=-8+b,解得b=10.∴一次函数的解析式为y=-x+10.20.【解】(1)根据题意得y=5(10-x),整理,得y=-5x+50.(2)0≤x<10.(3)如图所示.21.【解】(1)∵一次函数y=kx+b(k≠0)的图象由函数y=-x的图象平移得到,∴k=-1.将点(1,1)的坐标代入y=-x+b,解得b=2,∴一次函数的解析式是y=-x+2.(2)-1≤m≤2且m≠0.22.【解】(1)1 000×0.9=900(元),答:购买这张加油卡实际要付900元.(2)由题意知,y=0.9(x-0.30),整理得y=0.9x-0.27,∴y关于x的函数解析式为y=0.9x-0.27.(3)当x=7.30时,y=0.9×7.30-0.27=6.30,∵7.30-6.30=1.00(元/L),∴使用这张加油卡加油后油的单价比原价便宜1.00元/L.23.【解】(1)设直线AB的解析式为y=kx+b(k≠0).把点A(-8,19),B(6,5)的坐标分别代入y=kx+b,得-8k+b=19,6k+b=5,解得k=-1,b=11.∴AB所在直线的解析式为y=-x+11.(2)①由题意知,直线y=mx+n经过点C(2,0),∴2m+n=0.②设线段AB上的整点为(t,-t+11),则tm+n=-t+11,∵2m+n=0,∴(t-2)m=-t+11.易知t-2≠0.∴m=-t+11t-2=-1+9t-2.∵t为整数,m也是整数,∴t-2=±1或±3或±9.解得t=1,3,5,-1,-7或11.∵-8≤t≤6,∴t=11不符合题意,舍去.当t=1时,m=-10;当t=3时,m=8;当t=5时,m=2;当t=-1时,m=-4;当t=-7时,m=-2.∴符合题意的整数m的个数为5.24.【解】(1)由负到正(2)设轨道AB的长为n m,当滑块从左向右滑动时,∵l1+l2+1=n,∴l2=n-l1-1.∴d=l1-l2=l1-(n-l1-1)=2l1-n+1=2×9t-n+1=18t-n+1.∴d是t的一次函数.∵当t=4.5和5.5时,与之对应的d的两个值互为相反数,∴当t=5时,d=0.∴18×5-n+1=0.∴n=91.∴滑块从点A到点B所用的时间为(91-1)÷9=10(s).∵整个过程总用时27 s(含停顿时间),且当滑块右端到达点B时,滑块停顿2 s,∴滑块从B返回到A所用的时间为27-10-2=15(s).∴滑块返回的速度为(91-1)÷15=6(m/s),∴当12≤t≤27时,l2=6(t-12).此时l1=91-1-l2=90-6(t-12)=162-6t.∴d=l1-l2=162-6t-6(t-12)=-12t+234.∴滑块从点B到点A的滑动过程中,d与t的函数解析式为d=-12t+234.(3)当d=18时,有两种情况:①当0≤t≤10时,18t-90=18,解得t=6.②当12≤t≤27时,-12t+234=18,解得t=18.综上所述,当t为6或18时,d=18.
第十九章综合素质评价一、选择题(每题3分,共30分)1.(母题:教材P82习题T7)下列图象中,y不是x的函数的是( B )2.[2022·无锡]函数y=4-x中自变量x的取值范围是( D )A.x>4 B.x<4 C.x≥4 D.x≤43.[2023·清华附中期中]一次函数y=-2x+4的图象不经过( C )A.第一象限 B.第二象限 C.第三象限 D.第四象限4.[2023·长沙南雅中学期中]数形结合是解决数学问题常用的思想方法.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),根据图象可知,关于x的不等式x+b>kx+4的解集是( C )(第4题)A.x>3 B.x<3 C.x>1 D.x<15.如图是硝酸钾和氯化铵在水里的溶解度(g)与温度(℃)之间的对应关系,观察该图可知( D )(第5题)A.硝酸钾和氯化铵在水里的溶解度随温度的增大而减小B.硝酸钾和氯化铵在水里的溶解度相同时,温度大于20 ℃C.当温度为10 ℃时,硝酸钾的溶解度大于氯化铵的溶解度D.当温度为40 ℃时,硝酸钾的溶解度大于氯化铵的溶解度6.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( D )(第6题)A.y=2x+3 B.y=x-3 C.y=2x-3 D.y=-x+37.[2023·深圳外国语学校期中]一次函数y1=ax+b与一次函数y2=bx-a在同一平面直角坐标系中的图象大致是( D )8.如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为t,y1(细实线)表示铁桶中水面高度,y2(粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则y1,y2随时间t变化的函数图象大致为( C ) 9.[2023·雅安]在平面直角坐标系中,将函数y=x的图象绕坐标原点逆时针旋转90°,再向上平移1个单位长度,所得直线的函数解析式为( A )A.y=-x+1 B.y=x+1 C.y=-x-1 D.y=x-110.如图,一次函数y=x+2的图象与x轴,y轴分别交于点A,B,把直线AB绕点B顺时针旋转30°,交x轴于点C,则线段AC的长为( A )(第10题)A.6+2 B.32 C.2+3 D.3+2二、填空题(每题3分,共24分)11.请写出一个函数的解析式,使得它的图象经过点(2,0): y=x-2(答案不唯一) .12.(母题:教材P107复习题T2)一次函数y=x-2的图象与y轴的交点坐标是 (0,-2) .13.若点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,则y1-y2 > 0.(填“>”或“<”)14.[2023·成都外国语学校月考]如图,函数y=ax和y=kx+b的图象相交于点A,则关于x,y的方程组y=kx+b,y=ax的解为 x=-2,y=1 .(第14题)15.若直线y=2x+b与坐标轴围成的三角形的面积为6,则b= ±26 .16.若关于x的一元一次不等式组23x>x-1,4x+1≥a恰有3个整数解,且一次函数y=(a-2)x+a+1的图象不经过第三象限,则a的取值范围是 -1≤a≤1 .17.[2022·辽宁]如图,直线y=2x+4与x轴交于点A,与y轴交于点B,点D为OB的中点,▱OCDE的顶点C在x轴上,顶点E在直线AB上,则▱OCDE的面积为 2 .(第17题)18.为落实“双减”政策,某校利用课后服务时间举行趣味运动会,在直线跑道上,甲同学从A处匀速跑向B处,乙同学从B处匀速跑向A处,两人同时出发,到达各自终点后立即停止运动,设甲同学跑步的时间为x(s),甲、乙两人之间的距离为y(m),y与x之间的函数关系如图所示,则图中t的值是 403 .(第18题)三、解答题(19题8分,20,21题每题10分,22,23题每题12分,24题14分,共66分)19.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),求此一次函数的解析式.【解】设一次函数的解析式为y=kx+b(k≠0).∵一次函数的图象与直线y=-x+1平行,∴k=-1.∴一次函数的解析式为y=-x+b.∵一次函数的图象经过点(8,2),∴2=-8+b,解得b=10.∴一次函数的解析式为y=-x+10.20.(母题:教材P108复习题T9)把一个长10 cm,宽5 cm的长方形的长减少x cm,宽不变,得到的长方形的面积为y cm2.(1)请写出y与x之间的函数关系式;(2)请写出自变量x的取值范围;(3)画出函数的图象.【解】(1)根据题意得y=5(10-x),整理,得y=-5x+50.(2)0≤x<10.(3)如图所示.21.[2023·北师大实验中学期中]在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象由函数y=-x的图象平移得到,且经过点(1,1).(1)求这个一次函数的解析式;(2)当x<1时,对于x的每一个值,函数y=mx-1(m≠0)的值小于一次函数y=kx+b的值,直接写出m的取值范围.【解】(1)∵一次函数y=kx+b(k≠0)的图象由函数y=-x的图象平移得到,∴k=-1.将点(1,1)的坐标代入y=-x+b,解得b=2,∴一次函数的解析式是y=-x+2.(2)-1≤m≤2且m≠0.22.某加油站推出促销活动,一张加油卡的面值是1 000元,打九折出售,使用这张加油卡加油,油的单价降低0.30元/L.假设这张加油卡的面值能够一次性全部用完.(1)购买这张加油卡实际要付多少钱?(2)用这张加油卡加油后油的单价为y元/L,原价为x元/L,求y关于x的函数解析式(不用写出自变量的取值范围).(3)油的原价是7.30元/L,求用这张加油卡加油后油的单价比原价便宜多少?【解】(1)1 000×0.9=900(元),答:购买这张加油卡实际要付900元.(2)由题意知,y=0.9(x-0.30),整理得y=0.9x-0.27,∴y关于x的函数解析式为y=0.9x-0.27.(3)当x=7.30时,y=0.9×7.30-0.27=6.30,∵7.30-6.30=1.00(元/L),∴使用这张加油卡加油后油的单价比原价便宜1.00元/L.23.[2022·河北]如图,在平面直角坐标系中,线段AB的端点为A(-8,19),B(6,5).(1)求AB所在直线的解析式;(2)某同学设计了一个动画:在函数y=mx+n(m≠0,y≥0)中,分别输入m和n的值,便得到射线CD,其中C(c,0),当c=2时,会从C处弹出一个光点P,并沿CD飞行;当c≠2时,只发出射线而无光点弹出.①若有光点P弹出,试推算m,n应满足的数量关系;②当有光点P弹出,并击中线段AB上的整点(横、纵坐标都是整数)时,线段AB就会发光,求此时整数m的个数.【解】(1)设直线AB的解析式为y=kx+b(k≠0).把点A(-8,19),B(6,5)的坐标分别代入y=kx+b,得-8k+b=19,6k+b=5,解得k=-1,b=11.∴AB所在直线的解析式为y=-x+11.(2)①由题意知,直线y=mx+n经过点C(2,0),∴2m+n=0.②设线段AB上的整点为(t,-t+11),则tm+n=-t+11,∵2m+n=0,∴(t-2)m=-t+11.易知t-2≠0.∴m=-t+11t-2=-1+9t-2.∵t为整数,m也是整数,∴t-2=±1或±3或±9.解得t=1,3,5,-1,-7或11.∵-8≤t≤6,∴t=11不符合题意,舍去.当t=1时,m=-10;当t=3时,m=8;当t=5时,m=2;当t=-1时,m=-4;当t=-7时,m=-2.∴符合题意的整数m的个数为5.24.某动力科学研究院实验基地内装有一段笔直的轨道AB,长度为1m的金属滑块在上面做往返滑动.如图,滑块首先沿AB方向从左向右匀速滑动,滑动速度为9 m/s,滑动开始前滑块左端与点A重合,当滑块右端到达点B时,滑块停顿2 s,然后再以小于9 m/s的速度匀速返回,直到滑块的左端与点A重合,滑动停止.设滑块滑动的时间为t(s)时,滑块左端离点A的距离为l1(m),右端离点B的距离为l2(m),记d=l1-l2,d与t具有函数关系,已知滑块在从左向右滑动过程中,当t=4.5和5.5时,与之对应的d的两个值互为相反数;滑块从点A出发到最后返回点A,整个过程总用时27 s(含停顿时间).请你根据所给条件解决下列问题:(1)滑块从点A到点B的滑动过程中,d的值 由负到正 ;(填“由负到正”或“由正到负”)(2)滑块从点B到点A的滑动过程中,求d与t的函数解析式;(3)在整个往返过程中,若d=18,求t的值.【解】(2)设轨道AB的长为n m,当滑块从左向右滑动时,∵l1+l2+1=n,∴l2=n-l1-1.∴d=l1-l2=l1-(n-l1-1)=2l1-n+1=2×9t-n+1=18t-n+1.∴d是t的一次函数.∵当t=4.5和5.5时,与之对应的d的两个值互为相反数,∴当t=5时,d=0.∴18×5-n+1=0.∴n=91.∴滑块从点A到点B所用的时间为(91-1)÷9=10(s).∵整个过程总用时27 s(含停顿时间),且当滑块右端到达点B时,滑块停顿2 s,∴滑块从B返回到A所用的时间为27-10-2=15(s).∴滑块返回的速度为(91-1)÷15=6(m/s),∴当12≤t≤27时,l2=6(t-12).此时l1=91-1-l2=90-6(t-12)=162-6t.∴d=l1-l2=162-6t-6(t-12)=-12t+234.∴滑块从点B到点A的滑动过程中,d与t的函数解析式为d=-12t+234.(3)当d=18时,有两种情况:①当0≤t≤10时,18t-90=18,解得t=6.②当12≤t≤27时,-12t+234=18,解得t=18.综上所述,当t为6或18时,d=18. 第十九章综合素质评价一、1.B 【点拨】自变量x在取值范围内任取一个值,因变量y有唯一确定的值与之对应,则y是x的函数,A,C,D均满足任取一个x的值,有唯一确定的y值和它对应,则y是x的函数,而B中,x取一个正数,与之对应的有两个y值,故y不是x的函数,故选B.2.D 3.C 4.C 5.D 6.D7.D 【点拨】根据函数图象,确定a,b的正负,看看是否矛盾即可.8.C9.A 【点拨】在函数y=x的图象上取点A(1,1),绕原点逆时针方向旋转90°后得到对应的点的坐标为A'(-1,1),则旋转后的直线的解析式为y=-x.再向上平移1个单位长度,得到的直线的解析式为y=-x+1.10.A 【点拨】在一次函数y=x+2中,令x=0,则y=2;令y=0,则x=-2.∴A(-2,0),B(0,2).∴OA=OB=2.∴△OAB为等腰直角三角形,∠OAB=45°.∴AB=(2)2+(2)2=2.如图,过点C作CD⊥AB,垂足为点D.∵∠CAD=∠OAB=45°,∴△ACD为等腰直角三角形.设CD=AD=a,∴AC=AD2+CD2=2a.∵直线AB绕点B顺时针旋转30°得到直线CB,∴∠ABC=30°.∴BC=2CD=2a.∴BD=BC2-CD2=3a.又∵BD=AB+AD=2+a.∴2+a=3a,解得a=3+1.∴AC=2a=2(3+1)=6+2.二、11.y=x-2(答案不唯一)12.(0,-2)【点拨】根据一次函数的图象与y轴的交点的横坐标等于0,将x=0代入y=x-2,可得y的值,从而可以得到一次函数y=x-2的图象与y轴的交点坐标.13.>14.x=-2,y=1【点拨】根据图象可知,函数y=ax和y=kx+b的图象的交点A的坐标是(-2,1),所以关于x,y的方程组y=kx+b,y=ax的解为x=-2,y=1.15.±26 【点拨】已知直线与两坐标轴所围成的三角形的面积,求直线对应的函数解析式的方法:先设出直线对应的函数解析式,再用待定字母表示出直线与两坐标轴的交点坐标(注:这步中要考虑直线与x轴,y轴相交时的位置的不同情况),然后利用已知三角形的面积求出待定字母的值,最后代回所设函数解析式即可.16.-1≤a≤1 17.218.403【点拨】由图象和题意可知,乙在t s时到达A处,甲在20 s时到达B处,则V甲=8020=4(m/s),第8 s时两人相遇,则(V乙+4)×8=80.解得V乙=6 m/s,则6t=80,解得t=403.三、19.【解】设一次函数的解析式为y=kx+b(k≠0).∵一次函数的图象与直线y=-x+1平行,∴k=-1.∴一次函数的解析式为y=-x+b.∵一次函数的图象经过点(8,2),∴2=-8+b,解得b=10.∴一次函数的解析式为y=-x+10.20.【解】(1)根据题意得y=5(10-x),整理,得y=-5x+50.(2)0≤x<10.(3)如图所示.21.【解】(1)∵一次函数y=kx+b(k≠0)的图象由函数y=-x的图象平移得到,∴k=-1.将点(1,1)的坐标代入y=-x+b,解得b=2,∴一次函数的解析式是y=-x+2.(2)-1≤m≤2且m≠0.22.【解】(1)1 000×0.9=900(元),答:购买这张加油卡实际要付900元.(2)由题意知,y=0.9(x-0.30),整理得y=0.9x-0.27,∴y关于x的函数解析式为y=0.9x-0.27.(3)当x=7.30时,y=0.9×7.30-0.27=6.30,∵7.30-6.30=1.00(元/L),∴使用这张加油卡加油后油的单价比原价便宜1.00元/L.23.【解】(1)设直线AB的解析式为y=kx+b(k≠0).把点A(-8,19),B(6,5)的坐标分别代入y=kx+b,得-8k+b=19,6k+b=5,解得k=-1,b=11.∴AB所在直线的解析式为y=-x+11.(2)①由题意知,直线y=mx+n经过点C(2,0),∴2m+n=0.②设线段AB上的整点为(t,-t+11),则tm+n=-t+11,∵2m+n=0,∴(t-2)m=-t+11.易知t-2≠0.∴m=-t+11t-2=-1+9t-2.∵t为整数,m也是整数,∴t-2=±1或±3或±9.解得t=1,3,5,-1,-7或11.∵-8≤t≤6,∴t=11不符合题意,舍去.当t=1时,m=-10;当t=3时,m=8;当t=5时,m=2;当t=-1时,m=-4;当t=-7时,m=-2.∴符合题意的整数m的个数为5.24.【解】(1)由负到正(2)设轨道AB的长为n m,当滑块从左向右滑动时,∵l1+l2+1=n,∴l2=n-l1-1.∴d=l1-l2=l1-(n-l1-1)=2l1-n+1=2×9t-n+1=18t-n+1.∴d是t的一次函数.∵当t=4.5和5.5时,与之对应的d的两个值互为相反数,∴当t=5时,d=0.∴18×5-n+1=0.∴n=91.∴滑块从点A到点B所用的时间为(91-1)÷9=10(s).∵整个过程总用时27 s(含停顿时间),且当滑块右端到达点B时,滑块停顿2 s,∴滑块从B返回到A所用的时间为27-10-2=15(s).∴滑块返回的速度为(91-1)÷15=6(m/s),∴当12≤t≤27时,l2=6(t-12).此时l1=91-1-l2=90-6(t-12)=162-6t.∴d=l1-l2=162-6t-6(t-12)=-12t+234.∴滑块从点B到点A的滑动过程中,d与t的函数解析式为d=-12t+234.(3)当d=18时,有两种情况:①当0≤t≤10时,18t-90=18,解得t=6.②当12≤t≤27时,-12t+234=18,解得t=18.综上所述,当t为6或18时,d=18.
相关资料
更多









