2024九年级数学下学期期末综合素质评价试卷（人教版附答案）

这是一份2024九年级数学下学期期末综合素质评价试卷（人教版附答案），共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．[2023·南宁二中期中]计算sin 30°的值是( )
A．eq \r(3) B．eq \f(1,2) C．eq \f(\r(2),2) D．eq \f(\r(3),2)
2．(母题：教材P6练习T2)反比例函数y＝eq \f(－5,x)的图象位于( )
A．第一、三象限 B．第二、三象限 C．第二、四象限 D．第一、四象限
3．若△ABC∽△A′B′C′，其相似比为3∶2，则△ABC与△A′B′C′的周长比为( )
A．3∶2 B．9∶4 C．2∶3 D．4∶9
4．在Rt△ABC中，∠C＝90°，sin A＝eq \f(2,3)，则tan A的值为( )
A．eq \f(\r(5),3) B．eq \f(\r(5),2) C．eq \f(3,2) D．eq \f(2\r(5),5)
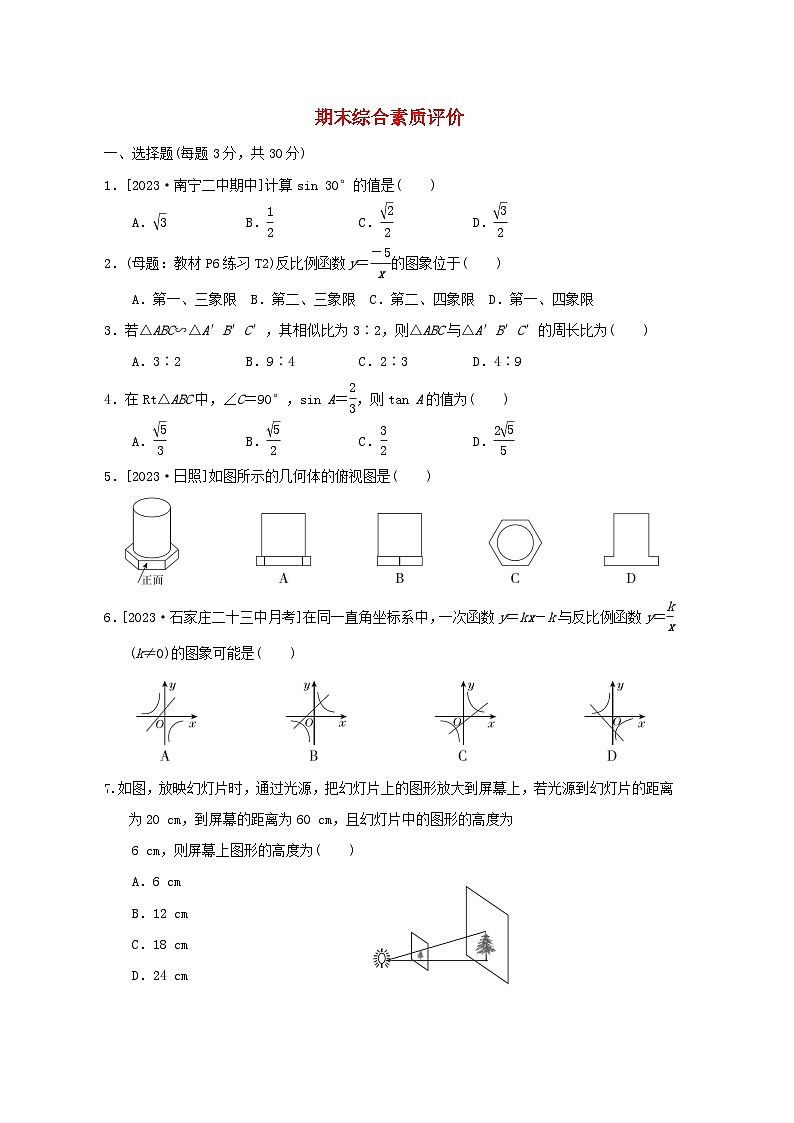
5．[2023·日照]如图所示的几何体的俯视图是( )
6．[2023·石家庄二十三中月考]在同一直角坐标系中，一次函数y＝kx－k与反比例函数y＝eq \f(k,x)(k≠0)的图象可能是( )
7.如图，放映幻灯片时，通过光源，把幻灯片上的图形放大到屏幕上，若光源到幻灯片的距离为20 cm，到屏幕的距离为60 cm，且幻灯片中的图形的高度为
6 cm，则屏幕上图形的高度为( )
A．6 cm
B．12 cm
C．18 cm
D．24 cm
8．如图，菱形ABCD的边长为6，E是AB的中点，CG平分∠ECD交BA的延长线于点G，交AD于点F，若CE＝CB，则AF的长是( )
A．4 B．3 C．2.5 D．2
9．如图，在一笔直的海岸线l上有A，B两个观测站，AB＝2 km.从A站测得船C在北偏东45°的方向，从B站测得船C在北偏东22.5°的方向，则船C离海岸线l的距离(即CD的长)为( )
A．4 km B．(2＋eq \r(2))km C．2eq \r(2)km D．(4－eq \r(2))km
10．[2023·苏州]如图，AB是半圆O的直径，点C，D在半圆上，eq \(CD,\s\up8(︵))＝eq \(DB,\s\up8(︵))，连接OC，CA，OD，过点B作EB⊥AB，交OD的延长线于点E.设△OAC的面积为S1，△OBE的面积为S2，若eq \f(S1,S2)＝eq \f(2,3)，则tan∠ACO的值为( )
A．eq \r(2) B．eq \f(2\r(2),3) C．eq \f(7,5) D．eq \f(3,2)
二、填空题(每题3分，共24分)
11.写出一个反比例函数y＝eq \f(k,x)(k≠0)，使它的图象在每个象限内，y的值随x值的增大而减小，这个函数的解析式为____________．
12．在△ABC中，|2cs A－1|＋(eq \r(3)－tan B)2＝0，则△ABC的形状是_______________．
13．如图，△ABC中，CD平分∠ACB，DE∥AC交BC于点E，若AC＝5，DE＝3，则BE＝________．
14．(母题：教材P41练习T1)在某一时刻，测得一根高为2 m的竹竿的影长为1 m，同时测得一栋建筑物的影长为12 m，那么这栋建筑物的高度为________m.
15．活动楼梯如图所示，∠B＝90°，斜坡AC的坡度为1∶1，斜坡AC的坡面长度为8 m，则走这个活动楼梯从A点到C点上升的高度BC为________．
16．(母题：教材P102习题T5)如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图，组成这个几何体的小正方体的个数是________________．
17．[2023·深圳]如图，Rt△OAB与Rt△OBC位于平面直角坐标系中，∠AOB＝∠BOC＝30°，BA⊥OA，CB⊥OB，若AB＝eq \r(3)，反比例函数y＝eq \f(k,x)(k≠0)的图象恰好经过点C，则k＝________．
18．已知如图，M(m，0)是x轴上的动点，⊙M的半径r＝2eq \r(2)，若⊙M与直线
y＝x＋2相交，则m的取值范围是__________．
三、解答题(19题6分，20题10分，24题14分，其余每题12分，共66分)
19．(母题：教材P69习题T3)计算：eq \r(3)tan 30°＋cs245°－(sin 30°－1)0.
20．如图，E为▱ABCD的边CD延长线上的一点，连接BE交AC于点O，交AD于点F.
(1)求证：△AOB∽△COE；
(2)求证：BO2＝EO·FO.
21．[2022·南充]如图，直线AB与双曲线交于A(1，6)，B(m，－2)两点，直线BO与双曲线在第一象限交于点C，连接AC．
(1)求直线AB与双曲线的解析式；
(2)求△ABC的面积．
22．由几个相同的边长为1的小立方块搭成的几何体的俯视图如图，方格中的数字表示该位置上小立方块的个数．
(1)请在如图的方格纸中分别画出该几何体的主视图和左视图；
(2)根据三视图，求这个几何体的表面积．
23．[2023·聊城]如图，在Rt△ABC中，∠ACB＝90°，∠BAC的平分线AD交BC于点D．∠ADC的平分线DE交AC于点E，以AD上的点O为圆心，OD为半径作⊙O，恰好过点E.
(1)求证：AC是⊙O的切线；
(2)若CD＝12，tan ∠ABC＝eq \f(3,4)，求⊙O的半径．
24．[2023·嘉兴]图①是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别)，其示意图如图②，摄像头A的仰角、俯角均为15°，摄像头高度OA＝160 cm，识别的最远水平距离OB＝150 cm.
(1)身高208 cm的小杜，头部高度为26 cm，他站在离摄像头水平距离130 cm的点C处，请问小杜最少需要下蹲多少厘米才能被识别？
(2)身高120 cm的小若，头部高度为15 cm，踮起脚尖可以增高3 cm，但仍无法被识别，社区及时将摄像头的仰角、俯角都调整为20°(如图③)，此时小若能被识别吗？请通过计算说明．(精确到0.1 cm，参考数据：sin 15°≈0.26，cs 15°≈0.97，tan 15°≈0.27，sin 20°≈0.34，cs 20°≈0.94，tan 20°≈0.36)
答案
一、1．B 2．C 3．A 4．D 5．C
6．C【点拨】分k＞0和k＜0讨论直线和双曲线在坐标系中的位置即可．
7．C
8．D【点拨】由菱形的性质、角平分线的定义，可得∠ECG＝∠G，由等角对等边可得CE＝EG，进而可得AG＝AE＝eq \f(1,2)EG＝eq \f(1,2)CD＝3，证明△GAF∽△CDF，则
eq \f(AF,DF)＝eq \f(AG,CD)，即eq \f(AF,6－AF)＝eq \f(3,6)，计算求解即可．
9．B
10．A 【点拨】如图，过点C作CH⊥AO于点H.
∵eq \(CD,\s\up8(︵))＝eq \(BD,\s\up8(︵))，∴∠COD＝∠BOE.
∵∠A＝eq \f(1,2)∠COB，
∴∠A＝∠BOE.
∵eq \f(S1,S2)＝eq \f(2,3)，即eq \f(\f(1,2)OA·CH,\f(1,2)OB·BE)＝eq \f(2,3)，
∴eq \f(CH,BE)＝eq \f(2,3).
∵∠A＝∠BOE，∴tan A＝tan∠BOE.
∴eq \f(CH,AH)＝eq \f(BE,OB)，即eq \f(CH,BE)＝eq \f(AH,OB)＝eq \f(2,3).
设AH＝2m，则BO＝3m＝AO＝CO，
∴OH＝3m－2m＝m.∴CH＝eq \r(9m2－m2)＝2eq \r(2)m.
∴tan A＝ eq \f(CH,AH)＝eq \f(2\r(2)m,2m)＝eq \r(2).
∵OA＝OC，∴∠A＝∠ACO.∴tan∠ACO＝eq \r(2).
故选A．
二、11．y＝eq \f(3,x)(答案不唯一)
12．等边三角形 【点拨】先根据非负数的性质得2cs A－1＝0，eq \r(3)－tan B＝0，再根据三角函数作答．
13．eq \f(9,2) 14．24 15．4eq \r(2) m
16．6或7或8
17．4eq \r(3) 【点拨】如图，过点C作CE⊥x轴，垂足为E.
∵BA⊥OA，CB⊥OB，∴∠OAB＝∠OBC＝90°.
∵∠AOB＝∠BOC＝30°，AB＝eq \r(3)，
∴OB＝2AB＝2eq \r(3)，BC＝eq \f(1,2)OC，∠COE＝90°－30°－30°＝30°.
在Rt△OBC中，OB2＋BC2＝OC2，∴12＋eq \f(1,4)OC2＝OC2.∴OC＝4.
∴CE＝eq \f(1,2)OC＝2，∴OE＝eq \r(OC2－CE2)＝2eq \r(3).
∴点C(2eq \r(3)，2)，∴k＝2eq \r(3)×2＝4eq \r(3).
18．－6＜m＜2 【点拨】如图，当点M′在x轴正半轴且⊙M′与直线y＝x＋2相切于点C时，设直线y＝x＋2与x轴，y轴分别交于B，A，连接CM′，
∴∠BCM′＝90°，CM′＝2eq \r(2)，A(0，2)，B(－2，0)．
∴AB＝eq \r(OA2＋OB2)＝2eq \r(2).
∵∠ABO＝∠M′BC，
∠AOB＝ ∠M′CB＝90°，
∴△AOB∽△M′CB．
∴eq \f(M′B,AB)＝eq \f(CM′,OA)，即eq \f(M′B,2\r(2))＝eq \f(2\r(2),2).
∴M′B＝4.∴OM′＝2.∴M′(2，0)．
同理可求出当M在x轴负半轴且⊙M与直线y＝x＋2相切时M的坐标为(－6，0)，∴当⊙M与直线y＝x＋2相交时，m的取值范围是－6三、19.【解】原式＝eq \r(3)×eq \f(\r(3),3)＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)))eq \s\up12(2)－1＝eq \f(1,2).
20．【证明】(1)∵四边形ABCD是平行四边形，
∴AB∥CD．
∴∠ABO＝∠CEO，∠BAO＝∠ECO.
∴△AOB∽△COE.
(2)∵△AOB∽△COE，
∴eq \f(OE,OB)＝eq \f(OC,OA).易得AD∥BC，
∴∠AFO＝∠CBO，∠FAO＝∠BCO.
∴△AOF∽△COB．
∴eq \f(OB,OF)＝eq \f(OC,OA).
∴eq \f(OE,OB)＝eq \f(OB,OF).
∴BO2＝EO·FO.
21．【解】(1)设双曲线的解析式为y＝eq \f(k,x).
∵点A(1，6)在该双曲线上，
∴6＝eq \f(k,1)，解得k＝6.
∴双曲线的解析式为y＝eq \f(6,x).
∵点B(m，－2)在双曲线y＝eq \f(6,x)上，
∴－2＝eq \f(6,m)，解得m＝－3.
∴B(－3，－2)．
设直线AB的解析式为y＝ax＋b，将A(1，6)，B(－3，－2)的坐标分别代入，
得eq \b\lc\{(\a\vs4\al\c1(a＋b＝6，,－3a＋b＝－2，))
解得eq \b\lc\{(\a\vs4\al\c1(a＝2，,b＝4.))
∴直线AB的解析式为y＝2x＋4.
(2)如图，作BG∥x轴，CG∥y轴，CG与BG交于点G，作BE∥y轴，AE∥x轴，BE与AE交于点E，EA的延长线与GC的延长线交于点F，则四边形EBGF为矩形．
由点B(－3，－2)可得直线BO的解析式为y＝eq \f(2,3)x.
解方程组eq \b\lc\{(\a\vs4\al\c1(y＝\f(2,3)x，,y＝\f(6,x)，))得eq \b\lc\{(\a\vs4\al\c1(x＝3，,y＝2))或eq \b\lc\{(\a\vs4\al\c1(x＝－3，,y＝－2.))
∴点C的坐标为(3，2)．
又∵A(1，6)，B(－3，－2)，
∴EB＝8，BG＝6，CG＝4，CF＝4，AF＝2，AE＝4.
∴S△ABC＝S矩形EBGF－S△AEB－S△BGC－S△AFC＝8×6－eq \f(4×8,2)－eq \f(6×4,2)－eq \f(4×2,2)＝48－16－12－4＝16.
22．【解】(1)画出的主视图与左视图如图．
(2)根据主视图可知，从前、后两个方向各看见5个小正方形；根据左视图可知，从左、右两个方向各看见4个小正方形；根据俯视图可知，从上、下两个方向各看见3个小正方形，∴这个几何体的表面积为1×1×(5＋4＋3)×2＝24.
23．(1)【证明】如图，连接OE，
∵OD＝OE，
∴∠OED＝∠ODE.
∵DE平分∠ADC，
∴∠CDE＝∠ODE.
∴∠OED＝∠CDE.∴OE∥CD．
∴∠AEO＝∠ACB．
∵∠ACB＝90°，∴∠AEO＝90°.
∴OE⊥AC．
∴AC是⊙O的切线．
(2)【解】如图，过D作DF⊥AB于F.
∵AD平分∠BAC，DF⊥AB，∠ACB＝90°，CD＝12，
∴DF＝CD＝12.
∵tan ∠ABC＝eq \f(3,4)，
∴BF＝eq \f(DF,tan ∠ABC)＝16.
∴BD＝eq \r(DF2＋BF2)＝20.
∴BC＝CD＋BD＝32.
∴AC＝BC·tan ∠ABC＝24.
∴AD＝eq \r(AC2＋CD2)＝12eq \r(5).
∵OE∥CD，∴∠AEO＝∠C，∠AOE＝∠ADC，
∴△AEO∽△ACD．∴eq \f(EO,CD)＝eq \f(AO,AD).
即eq \f(EO,12)＝eq \f(12\r(5)－OD,12\r(5))＝eq \f(12\r(5)－EO,12\r(5))，
解得EO＝15－3eq \r(5).
∴⊙O的半径为15－3eq \r(5).
24．【解】(1)如图①，过点C作OB的垂线，交仰角线于点E，交水平线于点F，则AF＝OC＝130 cm，CF＝OA＝160 cm，CE⊥AF.
在Rt△AEF中，tan∠EAF＝eq \f(EF,AF)，
∴EF＝AF·tan 15°≈130×0.27＝35.1(cm)．
∴CE＝CF＋EF≈160＋35.1＝195.1(cm)．
∴小杜最少需要下蹲约208－195.1＝12.9(cm)才能被识别．
(2)如图②，过点B作OB的垂线分别交仰角线、俯角线于M，N，交水平线于点P，则AP＝OB＝150 cm，BP＝OA＝160 cm.
在Rt△APM中，tan∠MAP＝eq \f(MP,AP).
∴MP＝AP·tan 20°≈150×0.36＝54.0(cm)．
∵∠MAP＝∠NAP，AP＝AP，∠APM＝∠APN＝90°，
∴△AMP≌△ANP(ASA)．
∴PN＝MP≈54.0 cm.
∴BN＝BP－PN≈160－54.0＝106.0(cm)．
∵小若踮起脚尖后头顶的高度为120＋3＝123(cm)，
∴小若头顶超出点N的高度约为123－106.0＝17.0(cm)>15 cm.
∴踮起脚尖小若能被识别．