
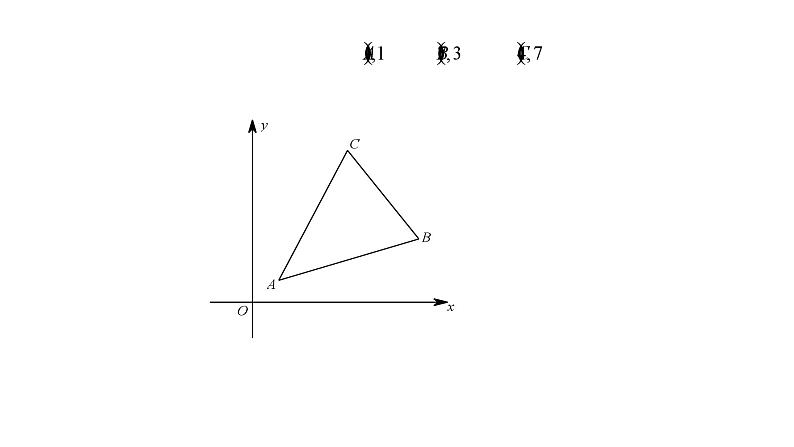


专题09 铅垂法求面积最值-2024年中考大招三轮冲刺课件PPT
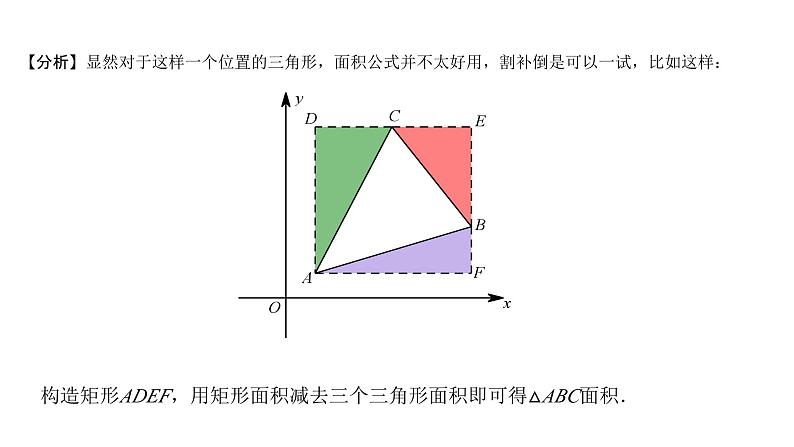
展开【分析】显然对于这样一个位置的三角形,面积公式并不太好用,割补倒是可以一试,比如这样:
构造矩形ADEF,用矩形面积减去三个三角形面积即可得△ABC面积.
此处AE+AF即为A、B两点之间的水平距离.
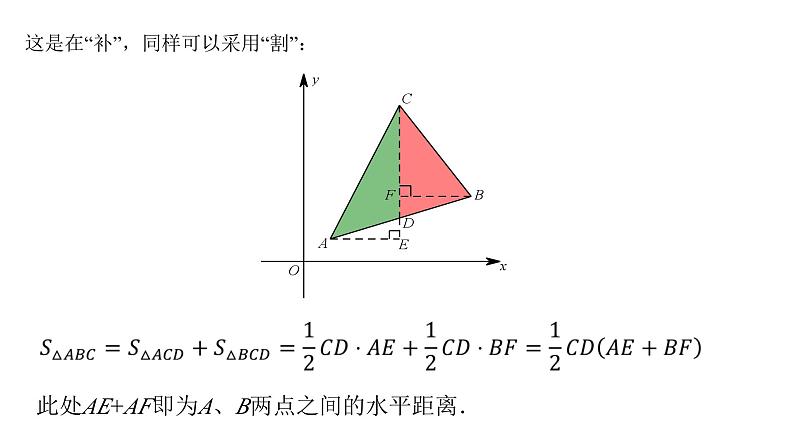
这是在“补”,同样可以采用“割”:
由题意得:AE+BF=6.
根据A、B两点坐标求得直线AB解析式为:
由点C坐标(4,7)可得D点横坐标为4,
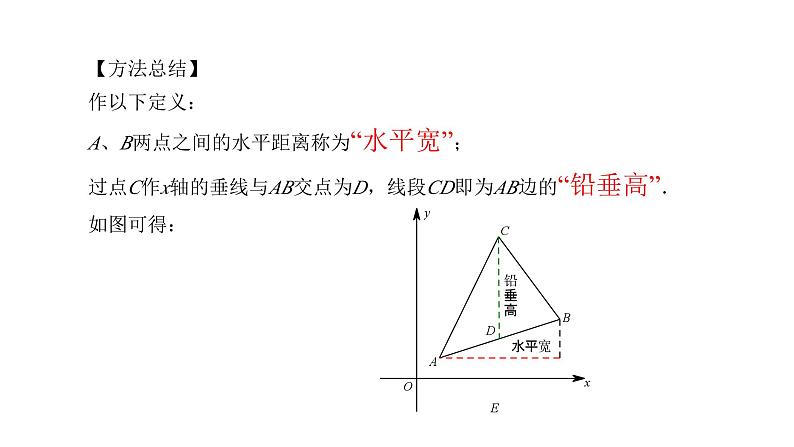
【方法总结】作以下定义:A、B两点之间的水平距离称为“水平宽”;过点C作x轴的垂线与AB交点为D,线段CD即为AB边的“铅垂高”.如图可得:
【解题步骤】(1)求A、B两点水平距离,即水平宽;(2)过点C作x轴垂线与AB交于点D,可得点D横坐标同点C;(3)求直线AB解析式并代入点D横坐标,得点D纵坐标;(4)根据C、D坐标求得铅垂高;(5)利用公式求得三角形面积.
【小结】选两个定点作水平宽,设另外一个动点坐标来表示铅垂高.
【思考】如果第3个点的位置不像上图一般在两定点之间,如何求面积? 铅垂法其实就是在割补,重点不在三个点位置,而是取两个点作水平宽之后,能求出其对应的铅垂高!因此,动点若不在两定点之间,方法类似:
【铅垂法大全】(1)取AB作水平宽,过点C作铅垂高CD.
(2)取AC作水平宽,过点B作BD⊥x轴交直线AC于点D,BD即对应的铅垂高,
(3)取BC作水平宽,过点A作铅垂高AD.
甚至,还可以横竖互换,在竖直方向作水平宽,在水平方向作铅垂高.(4)取BC作水平宽,过点A作铅垂高AD.
(5)取AC作水平宽,过点B作铅垂高BD.
(6)取AB作水平宽,过点C作铅垂高CD.
说这么多做法也不是要记住的,基本上从(3)开始往后都是用不上的,用以帮助我们了解铅垂法的解题原理,再来看个例子巩固下.
专题04 隐形圆-2024年中考大招三轮冲刺课件PPT: 这是一份专题04 隐形圆-2024年中考大招三轮冲刺课件PPT,共55页。PPT课件主要包含了定边对直角,定边对定角角等内容,欢迎下载使用。
专题03 将军饮马(二)-2024年中考大招三轮冲刺课件PPT: 这是一份专题03 将军饮马(二)-2024年中考大招三轮冲刺课件PPT,共20页。PPT课件主要包含了将军过桥,将军遛马等内容,欢迎下载使用。
中考数学二轮专题复习铅垂法求二次函数中三角形面积的最值专训: 这是一份中考数学二轮专题复习铅垂法求二次函数中三角形面积的最值专训,共5页。












