贵州省黔东南苗族侗族自治州榕江县朗洞镇初级中学2023-2024学年八年级下学期3月月考数学试题（原卷版+解析版）

这是一份贵州省黔东南苗族侗族自治州榕江县朗洞镇初级中学2023-2024学年八年级下学期3月月考数学试题（原卷版+解析版），文件包含精品解析贵州省黔东南苗族侗族自治州榕江县朗洞镇初级中学2023-2024学年八年级下学期3月月考数学试题原卷版docx、精品解析贵州省黔东南苗族侗族自治州榕江县朗洞镇初级中学2023-2024学年八年级下学期3月月考数学试题解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。

（时间：120分钟 满分：150分）
一、选择题（以下每小题均有四个选项，其中只有一个选项正确，每小题3分，共36分）
1. 老师在黑板上写了下列式子：①；②；③；④；⑤；⑥．你认为其中是不等式的有（ ）
A. 2个B. 3个C. 4个D. 5个
【答案】C
【解析】
【分析】根据不等式的定义，依次分析即可．
【详解】解：∵用不等号表示大小关系的式子叫做不等式，其中常用不等号有：“”，
∴属于不等式的为：，共有4个．
故选：C
【点睛】本题主要考查不等式的定义，用“”或“”或“”或“”号表示大小关系的式子，叫做不等式，用“”号表示不等关系的式子也是不等式．
2. 若，则下列不等式不一定成立的是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】不等式的基本性质1，在不等式的两边都加上或减去同一个数或整式，不等号的方向不变，根据不等式的基本性质2，在不等式的两边都乘以或除以同一个正数，不等号的方向不变，不等式的基本性质3，在不等式的两边都乘以或除以同一个负数，不等号的方向改变，根据不等式的基本性质逐一分析判断即可．
【详解】解：∵，
∴，，，故A，B，D不符合题意，
∵当a=-2,b=-3时，a2小于b2,故C符合题意，
故选C
【点睛】本题考查的是不等式的基本性质，掌握“不等式的基本性质”是解本题的关键．
3. 不等式组2x＞﹣2的解集在数轴上表示正确的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】先求出不等式的解集，再表示在数轴上即可．
【详解】解：解不等式2x＞﹣2，得：x＞﹣1，在数轴上表示为：
故选：A．
【点睛】本题考查了一元一次不等式的解法，熟练掌握解一元一次不等式的步骤是解答本题的关键．不等式的解集在数轴上表示时，空心圈表示不包含该点，实心点表示包含该点．
4. 将不等式去分母，正确的是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】根据不等式性质2，两边都乘以分母最小公倍数4可得．
【详解】解：不等式两边都乘以分母的最小公倍数4，得：，
即：，
故选：D．
【点睛】本题主要考查不等式的基本性质2，去分母时要注意不等式两边都乘以或除以同一个不为0的数，当是负数时不等号方向要改变．
5. 若等腰三角形的周长为10 cm，其中一边长为2 cm，则该等腰三角形的底边长为（ ）
A. 2 cmB. 4 cmC. 6 cmD. 8 cm
【答案】A
【解析】
【详解】若2cm为等腰三角形的腰长，则底边长为10﹣2﹣2=6（cm），2+2＜6，不符合三角形的三边关系；
若2cm为等腰三角形的底边，则腰长为（10﹣2）÷2=4（cm），此时三角形的三边长分别为2cm，4cm，4cm，符合三角形的三边关系；
故选A．
6. 如图，在△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，若AC＝6，BC＝8，则CD等于（ ）
A. 1B. 2C. 3D. 4.8
【答案】D
【解析】
【详解】试题分析：根据勾股定理可求得AB=10，然后根据三角形的面积可得，解得CD=4.8.
故选D
7. 如图，已知△ABC（AC＜AB），用尺规在AB上确定一点P，使PB＋PC＝AB，则符合要求的作图痕迹是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】利用PB+PC=AB，PB+PA=AB，得到PC=PA，根据线段垂直平分线的判定定理，得到点P在线段AC的垂直平分线上，由此可知选项C符合题意．
【详解】解：∵点P在AB上，∴PB+PA=AB，
又∵PB+PC=AB，∴PC=PA，
∴点P在线段AC的垂直平分线上，
且线段AC的垂直平分线交AB于点P．
∴选项C符合要求，
故选：C．
【点睛】本题考查了线段垂直平分线的尺规作图，结合几何图形的基本性质把AB拆成PA与PB之和进而得到PC=PA是解决本题的关键．
8. 如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8 m处，发现此时绳子末端距离地面2 m，则旗杆的高度(滑轮上方的部分忽略不计)为( )
A. 12 mB. 13 mC. 16 mD. 17 m
【答案】D
【解析】
【分析】根据题意画出示意图，设旗杆高度为x，可得AC=AD=x，AB=（x﹣2）m，BC=8m，在Rt△ABC中利用勾股定理可求出x．
【详解】解：设旗杆高度为x，则AC=AD=x，AB=（x﹣2）m，BC=8m，
在Rt△ABC中，AB2+BC2=AC2，即（x﹣2）2+82=x2，
解得：x=17，
即旗杆的高度为17米．
故选D．
【点睛】本题考查了勾股定理的应用，解答本题的关键是构造直角三角形，构造直角三角形的一般方法就是作垂线．
9. 如图，直线l1∥l2，将等边三角形如图放置若∠α＝25°，则∠β等于（ ）
A. 35°B. 30°C. 25°D. 20°
【答案】A
【解析】
【分析】过点B作BD∥l1，如图，根据平行线的性质可得∠ABD＝∠β．根据平行线的传递性可得BD∥l2，从而得到∠DBC＝∠α＝35°．再根据等边△ABC可得到∠ABC＝60°，就可求出∠DBC，从而解决问题．
【详解】解：过点B作BD∥l1，如图，
则∠CBD＝∠β．
∵l1∥l2，
∴BD∥l2，
∵∠DBA＝∠α＝35°．
∵△ABC是等边三角形，
∴∠ABC＝60°，
∴∠β＝∠CBD＝∠ABC﹣∠DBA＝60°﹣25°＝35°．
故选A．
【点睛】本题主要考查了平行线的性质、平行线的传递性、等边三角形的性质等知识，当然也可延长BA与l2交于点E，运用平行线的性质及三角形外角的性质解决问题．
10. 如图，在四边形中，，，连接，，，若点P是边上一动点，则长的最小值为（ ）
A. 4B. 6C. 3D. 12
【答案】B
【解析】
【分析】本题考查了三角形内角和定理，角平分线的判定和性质定理，垂线段最短，掌握角平分线上的点到角两边的距离相等是解题关键．由三角形内角和定理，推出，由垂线段最短可知，当时，的长度最小，再利用角平分线的性质定理，得到，即可得到答案．
【详解】解：，
，
，
，
，
，
，即平分，
由垂线段最短可知，当时，的长度最小，
，，
，
，
的最小值是6，
故选：B．
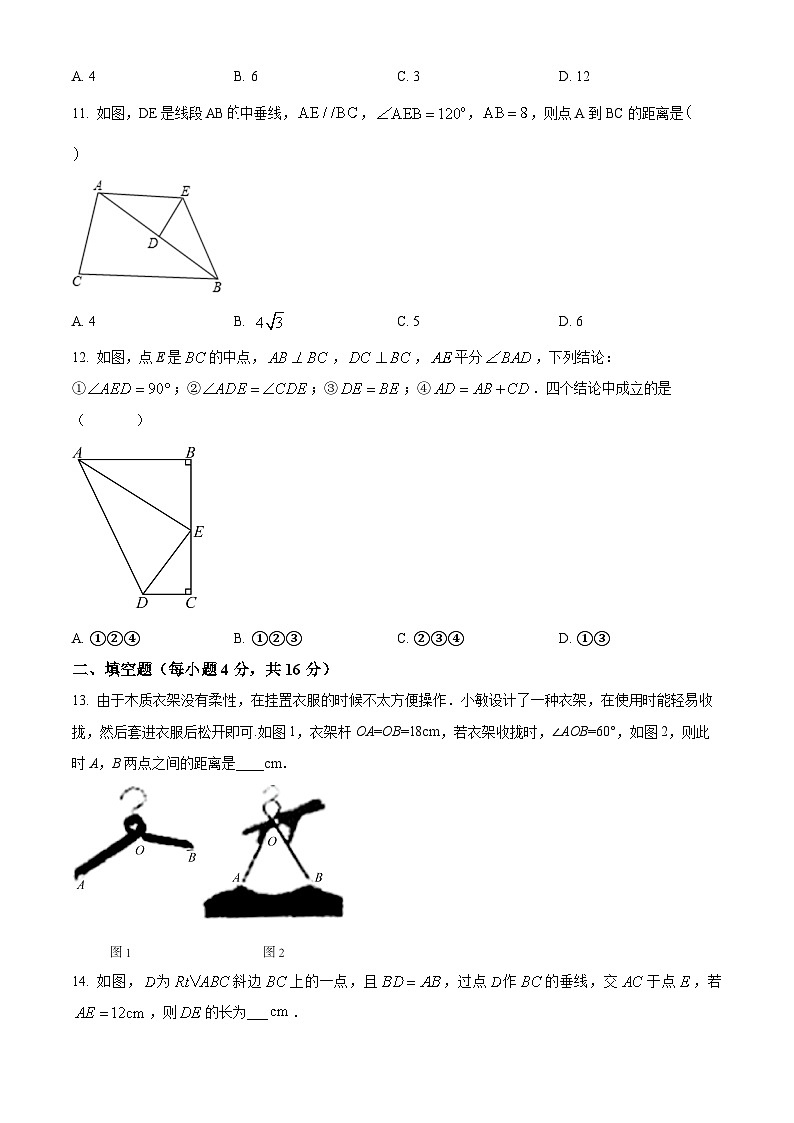
11. 如图，DE是线段AB的中垂线，，，，则点A到BC的距离是
A. 4B. C. 5D. 6
【答案】A
【解析】
【分析】作于利用直角三角形30度角的性质即可解决问题．
【详解】解：作于H．
垂直平分线段AB，
，
，
，
，
，
，
，，
，
故选A．
【点睛】本题考查线段的垂直平分线的性质，等腰三角形的性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．
12. 如图，点E是的中点，，，平分，下列结论：①；②；③；④．四个结论中成立的是（ ）

A. ①②④B. ①②③C. ②③④D. ①③
【答案】A
【解析】
【分析】过E作于F，可得，运用全等三角形的判定可得，再运用全等三角形的性质可得，；运用点E是的中点即可判断③是否正确；运用全等三角形的判定可得，再运用全等三角形的性质即可判断②④是否正确；运用即可判断①是否正确
【详解】解：过E作于F，如图，

∵，平分，
∴，
在和中， ，
∴，
∴，，
∵点E是中点，
∴，
而，，故③错误；
在和中，，
∴，
∴，，，故②正确；
∴，故④正确；
∴，故①正确．
因此正确的有①②④，
故选：A．
【点睛】本题考查全等三角形的判定与性质，角平分线的性质，解决本题的关键是得到．侧重考查知识点的理解、应用能力．学生在日常学习中应从以下3个方向（【逻辑推理】【直观想象】【数学运算】）培养对知识点的理解、应用能力．
二、填空题（每小题4分，共16分）
13. 由于木质衣架没有柔性，在挂置衣服的时候不太方便操作．小敏设计了一种衣架，在使用时能轻易收拢，然后套进衣服后松开即可.如图1，衣架杆OA=OB=18cm，若衣架收拢时，∠AOB=60°，如图2，则此时A，B两点之间的距离是____cm．
【答案】18
【解析】
【分析】根据有一个角是60°的等腰三角形的等边三角形进行解答即可．
【详解】解：∵OA=OB，∠AOB=60°，
∴△AOB是等边三角形，
∴AB=OA=OB=18cm
故答案为：18．
【点睛】此题考查等边三角形问题，关键是根据有一个角是60°的等腰三角形的等边三角形进行分析．
14. 如图，为斜边上的一点，且，过点作的垂线，交于点，若，则的长为___．
【答案】
【解析】
【分析】根据“”，得出，再根据全等三角形的性质，即可得出答案．
【详解】解：∵，
∴，
在和中，
，
∴，
∴，
又∵，
∴．
故答案为：
【点睛】本题考查了全等三角形的判定与性质，解本题的关键在证明．
15. 如图所示，在中，，，若，则的大小为_____．

【答案】##70度
【解析】
【分析】本题考查了平行线的性质，等腰三角形的性质，掌握等边对等角是解题关键．根据两直线平行，同旁内角互补，得到，再利用等边对等角的性质，即可求出的大小．
【详解】解：，
，
，
，
，
故答案为：．
16. 一次函数与的图象如图，则下列结论：①；②；③当时，；④．其中正确结论是___________(填序号)．
【答案】①③
【解析】
【分析】根据一次函数的性质对①②④进行判断；当x＜4时，根据两函数图象的位置对③进行判断．
【详解】解：根据图象y1=kx+b经过第一、二、四象限，
∴k＜0，b＞0，
故①正确，④错误；
∵y2=x+a与y轴负半轴相交，
∴a＜0，
故②错误；
当x＞4时图象y1在y2的下方，所以y1＜y2，故③正确．
所以正确的有①③．
故答案为：①③．
【点睛】此题主要考查了一次函数，以及一次函数与不等式，根据函数图象的走势和与y轴的交点来判断各个函数k，b的值．
三、解答题（本大题9小题，共98分．解答应写出必要的文字说明、证明过程或演算步骤）
17. 用适当的不等式表示下列不等关系：
（1）x减去6大于12；
（2）x的2倍与5的差是负数；
（3）x的3倍与4的和是非负数；
（4）y的5倍与9的差不大于；
【答案】（1）x-6＞12；（2）2x-5＜0；（3）3x+4≥0；（4）5y-9≤-1．
【解析】
【分析】（1）根据x减去6得出x-6，再根据x减去6大于12得出答案；
（2）先表示出x2倍为2x，再表示出与5的差为2x-5，列出不等式即可；
（3）先表示出x的3倍为3x，再表示出与41的和为3x+4，列出不等式即可；
（4）先表示出y的5倍是5y，再表示出与9的差5y-9，然后根据不大于-1即为小于等于-1，列出不等式即可．
【详解】（1）由题意可得：x-6＞12；
（2）由题意可得：2x-5＜0；
（3）由题意可得：3x+4≥0；
（4）由题意可得：5y-9≤-1．
【点睛】本题考查了由实际问题抽象出一元一次不等式，弄清运算的先后顺序和不等关系，才能把文字语言的不等关系转化为用数学符号表示的不等式．
18. 用反证法求证：三角形的一个外角等于与它不相邻的两个内角的和．
已知：如图，∠1是△ABC的一个外角．
求证：∠1＝∠A+∠B．

【答案】见解析
【解析】
【分析】首先假设三角形的一个外角不等于与它不相邻的两个内角的和，根据三角形的内角和等于180°，得到矛盾，所以假设不成立，进而证明三角形的一个外角等于与它不相邻的两个内角的和．
【详解】已知：如图，∠1是△ABC的一个外角，
求证：∠1＝∠A+∠B，
证明：假设∠1≠∠A+∠B，
在△ABC中，∠A+∠B+∠2＝180°，如下图所示：

∴∠A+∠B＝180°﹣∠2，
∵∠1+∠2＝180°，
∴∠1＝180°﹣∠2，
∴∠1＝∠A+∠B，
与假设相矛盾，
∴假设不成立，
∴原命题成立即：∠1＝∠A+∠B．
【点睛】本题考查了反证法的运用，反证法的一般解题步骤是：①假设命题的结论不成立；②从这个假设出发，经过推理论证，得出矛盾；③由矛盾判定假设不正确，从而肯定原命题的结论正确．
19. 如图，树垂直于地面，为测树高，小明在处，测得，他沿方向走到处，线段米，测得，求树高度．
【答案】米
【解析】
【分析】根据三角形外角的性质得到，根据等腰三角形的性质得到米，由直角三角形的性质即可得到结论．
【详解】解：，，
，
，
（米），
又，
（米），
∴树的高度为米．
【点睛】本题考查了含角的直角三角形的性质，等角对等边，三角形的外角的性质，熟练掌握含角的直角三角形的性质是解题的关键．
20. 如图，已知中，，，是的角平分线，于E点．
（1）求的度数；
（2）若，，，求．
【答案】（1）
（2）108
【解析】
【分析】（1）先根据三角形的内角和求出的度数，再根据角平分线的定义，得出的度数，最后根据直角三角形两个锐角互余，即可求解；
（2）过点作于点F，根据是的角平分线，，，得出，最后个根据即可求解．
【小问1详解】
解：∵，，
∴，
∵是的角平分线，
∴，
∵，
∴．
【小问2详解】
解∶过点作于点F，
∵是的角平分线，，，
∴，
∴．
【点睛】本题主要考查了三角形的内角和定理，角平分线的定义和性质，解题的关键是掌握三角形的内角和为，角平分线上的点到两边的距离相等．
21. 如图所示，为等边三角形，，点O为线段上一点，的延长线与的延长线交于点，．
（1）写出一对相等的角；
（2）求证：是等边三角形；
（3）若，，求的长．
【答案】（1）
（2）见解析 （3）2
【解析】
【分析】本题考查了平行线的性质，等边三角形的判定和性质，全等三角形的判定和性质，掌握全等三角形的性质是解题关键．
（1）根据平行线的性质写出一对等角即可；
（2）根据等边三角形的性质和平行线的性质，即可证明结论；
（3）证明，得到，，再结合等边三角形的性质，即可求出的长．
【小问1详解】
解：，
（答案不唯一）；
小问2详解】
证明：为等边三角形，
，
，
，，
，
是等边三角形；
【小问3详解】
解：，
，
在和中，
，
，
，，
和均是等边三角形，
，，
，
．
22. 如图，在△ABC中，∠B＝30°，∠C＝40°．
（1）尺规作图：①作边AB的垂直平分线交BC于点D；
②连接AD，作∠CAD的平分线交BC于点E；（要求：保留作图痕迹，不写作法）
（2）在（1）所作的图中，求∠DAE的度数．
【答案】（1）①见解析；②见解析；（2）∠DAE∠DAC＝40°
【解析】
【分析】（1）根据垂直平分线与角平分线的尺规作图方法即可求解；
（2）根据垂直平分线的性质得到DB＝DA，求出∠CAD=80°，再利用角平分线的性质即可求解．
【详解】解：（1）如图，点D，射线AE即为所求．
（2）∵DF垂直平分线段AB
∴DB＝DA
∴∠DAB＝∠B＝30°
∵∠C＝40°
∴∠BAC＝180°﹣30°﹣40°＝110°
∴∠CAD＝110°﹣30°＝80°
∵AE平分∠DAC
∴∠DAE∠DAC＝40°．
【点睛】此题主要考查垂直平分线与角平分线，解题的关键是熟知尺规作图的方法．
23. 笔直的河流一侧有一旅游地点，河边有两个漂流点、，且点到点的距离等于点到点的距离．近阶段由于点到点的路线处于维修中，为方便游客决定在河边新建一个漂流点（点在同一条直线上），并新建一条路，测得，，．
（1）判断的形状，并说明理由；
（2）求原路线长．
【答案】（1）是直角三角形，理由见解析
（2）
【解析】
【分析】（1）根据勾股定理的逆定理解答即可；
（2）根据题意，得出，再根据（1）可知是直角三角形，然后设，则，再根据勾股定理，列出关于的方程，解出即可得出的长．
【小问1详解】
解：是直角三角形，理由如下：
∵，，，
∴，
∴，
∴是直角三角形；
【小问2详解】
解：∵点到点的距离等于点到点的距离，
∴，
∵由（1）易知是直角三角形，
设，则，
在中，
，，，
∵，
∴，
解得：，
∴．
【点睛】本题考查了勾股定理及其逆定理的应用，解本题的关键在熟练掌握勾股定理的逆定理．
24. 如图，在△ABC中，AB＝AC，D为BC上一点，∠B＝30°，连接AD．
（1）若∠BAD＝45°，求证：△ACD为等腰三角形；
（2）若△ACD为直角三角形，求∠BAD的度数．
【答案】（1）见解析 (2) ∠BAD=60°或∠BAD=30°
【解析】
【分析】（1）根据等腰三角形的性质求出∠B=∠C=30°，根据三角形内角和定理求出∠BAC=120°，求出∠CAD=∠ADC，根据等腰三角形的判定得出即可；
（2）有两种情况：①当∠ADC=90°时，当∠CAD=90°时，求出即可．
【详解】（1）∵AB=AC，∠B=30°，
∴∠B=∠C=30°，
∴∠BAC=180°﹣30°﹣30°=120°，
∵∠BAD=45°，
∴∠CAD=∠BAC﹣∠BAD=120°﹣45°=75°，∠ADC=∠B+∠BAD=75°，
∴∠ADC=∠CAD，
∴AC=CD，
即△ACD为等腰三角形；
（2）有两种情况：①当∠ADC=90°时，
∵∠B=30°，
∴∠BAD=∠ADC﹣∠B=90°﹣30°=60°；
②当∠CAD=90°时，∠BAD=∠BAC﹣∠CAD=120°﹣90°=30°；
即∠BAD的度数是60°或30°．
25. （1）阅读理解：如图①，在中，，，，垂足分别为，，且，与交于点．图中与全等的三角形是 ，与全等的三角形是 ；
（2）问题探究：如图②，在中，，，平分，，垂足为．探究线段，，之间的关系，并证明；
（3）问题解决：如图③，在中，，，平分，交的延长线于点．求证：．

【答案】（1），；（2），见解析；（3）见解析
【解析】
【分析】（1）由“”可证，由“”可证；
（2）由“”可证，可得，，可得结论；
（3）由“”可证，可得，由“”可证，可得，可得结论．
【详解】（1）解：，
，
，，
，
，
，
，
，
又，
，
故答案为：，；
（2），理由如下：
，，
，
，
，
，
平分，
，
又，，
，
，，
；
（3）如图，延长，交于点，

平分，
，
又，，
，
，
，
，
，
又，，
，
，
．
【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，等腰直角三角形的性质，添加恰当辅助线构造全等三角形是解题的关键．