广东省深圳市2023-2024学年九年级下学期3月质量检测数学试题（33校联考）

这是一份广东省深圳市2023-2024学年九年级下学期3月质量检测数学试题（33校联考），共20页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

1．2024的倒数是
A．2024B．C．D．
2．2023年“亚运双节”让杭州火出圈，相关数据显示，国庆期间杭州共接待游客约13000000人次，将数据13000000用科学记数法表示为
A．B．C．D．
3．第19届亚运会于9月23日至10月8日在杭州成功举办，下列图形中是轴对称图形的是
A． B． C． D．
4．如图是我们生活中常用的“空心卷纸”，其主视图为
A．B．C．D．
5．“立身以立学为先，立学以读书为本．”为了鼓励全民阅读，某校图书馆开展阅读活动，自阅读活动开展以来，进馆阅读人次逐月增加，第一个月进馆200人次，前三个月累计进馆728人次，若进馆人次的月增长率相同，求进馆人次的月增长率．设进馆人次的月增长率为，依题意可列方程
A．B．
C． D．
6．下列计算正确的是
A．B．C．D．
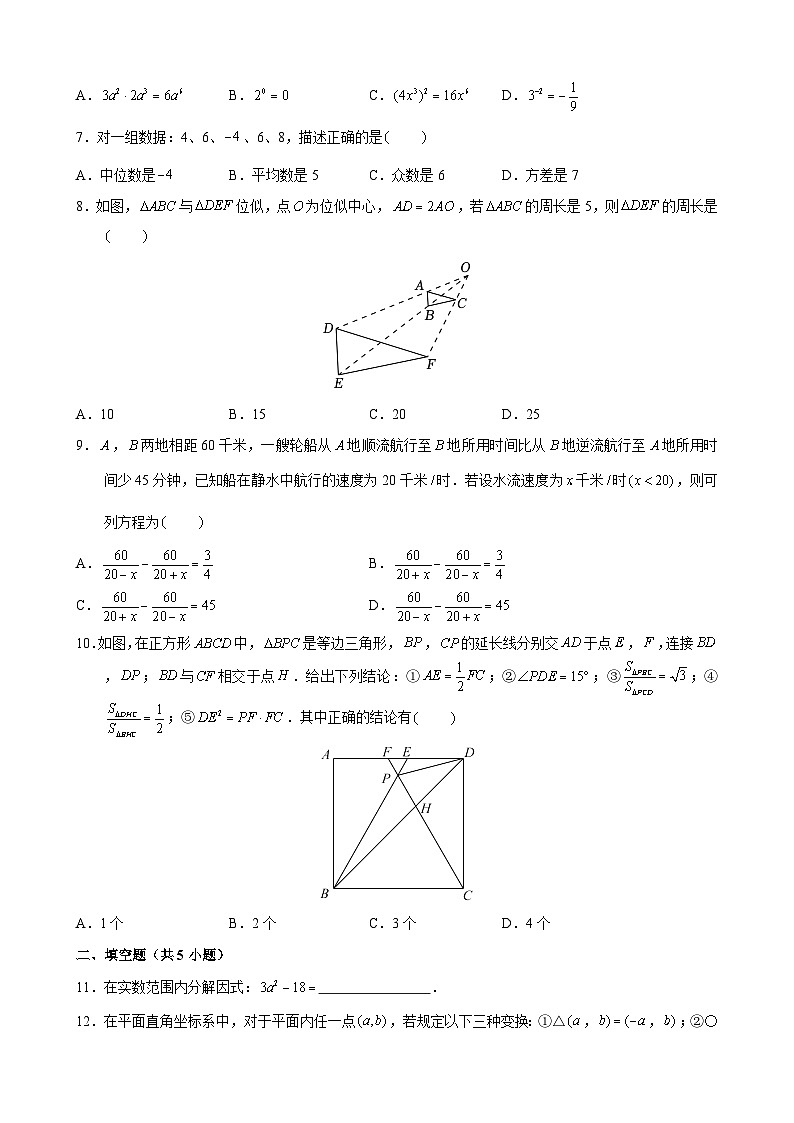
7．对一组数据：4、6、、6、8，描述正确的是
A．中位数是B．平均数是5C．众数是6D．方差是7
8．如图，与位似，点为位似中心，，若的周长是5，则的周长是
A．10B．15C．20D．25
9．，两地相距60千米，一艘轮船从地顺流航行至地所用时间比从地逆流航行至地所用时间少45分钟，已知船在静水中航行的速度为20千米时．若设水流速度为千米时，则可列方程为
A．B．
C．D．
10．如图，在正方形中，是等边三角形，，的延长线分别交于点，，连接，；与相交于点．给出下列结论：①；②；③；④；⑤．其中正确的结论有
A．1个B．2个C．3个D．4个
二、填空题（共5小题）
11．在实数范围内分解因式： ．
12．在平面直角坐标系中，对于平面内任一点，若规定以下三种变换：①△，，；②〇，，；③，，，按照以上变换例如：△〇，，，则〇等于 ．
13．如图，是反比例函数的图象上一点，过点作轴于点，点在轴上，且，则的值为 ．
14．如图，已知，以点为圆心，以任意长为半径画弧，与、分别于点、，再分别以点、为圆心，以大于为半径画弧，两弧相交于点，过上一点作，与相交于点，，则 ．
15．如图，在直角坐标系中，已知点，点为轴正半轴上一动点，连接，以为一边向下作等边，连接，则的最小值为 ．
三．解答题（共55分）
16．（5分）计算：．
17．（6分）化简求值：，其中为数据4，5，6，5，3，2的众数．
18．（8分）某校为了调查本校学生对航空航天知识的知晓情况，开展了航空航天知识竞赛，从参赛学生中，随机抽取若干名学生的成绩进行统计，得到如下不完整的统计图表：
请根据图表信息解答下列问题：
（1）求，，的值；
（2）补全频数分布直方图；
（3）某班有2名男生和1名女生的成绩都为100分，若从这3名学生中随机抽取2名学生参加演讲，用列表或画树状图的方法，求抽取的2名学生恰好为1男1女的概率．
19．（8分）如图，是的外接圆，直径与交于点，点在的延长线上，连接，．
（1）求证：是的切线；
（2）从以下三个选项中选一个作为条件，使成立，并说明理由；
①；
②；
③；
你选的条件是： ．
20．（8分）某经销商销售一种成本价为10元的商品，已知销售价不低于成本价，且物价部门规定这种产品的销售价不得高于18元．如图，在销售过程中发现销量与售价（元之间满足一次函数关系．
（1）求与之间的函数关系式，并写出自变量的取值范围；
（2）设销售这种商品每天所获得的利润为元，求与之间的函数关系式，并求出该商品售价定为多少元时，才能使经销商所获利润最大？最大利润是多少？
21．（9分）如图1，一灌溉车正为绿化带浇水，喷水口离地竖直高度为米．建立如图2所示的平面直角坐标系，可以把灌溉车喷出水的上、下边缘抽象为两条抛物线的部分图象，把绿化带横截面抽象为矩形，其水平宽度米，竖直高度米，下边缘抛物线是由上边缘抛物线向左平移得到，上边缘抛物线最高点离喷水口的水平距离为2米，高出喷水口0.4米，灌溉车到绿化带的距离为米．
（1）求上边缘抛物线喷出水的最大射程；
（2）求下边缘抛物线与轴交点的坐标；
（3）若米，灌溉车行驶时喷出的水 （填“能”或“不能” 浇灌到整个绿化带，并说明理由．
22．（11分）在矩形中，点是射线上一动点，连接，过点作于点，交直线于点．
（1）当矩形是正方形时，以点为直角顶点在正方形的外部作等腰直角三角形，连接．
①如图1，若点在线段上，则线段与之间的数量关系是 ，位置关系是 ；
②如图2，若点在线段的延长线上，①中的结论还成立吗？如果成立，请给予证明；如果不成立，请说明理由；
（2）如图3，若点在线段上，以和为邻边作平行四边形，是中点，连接，，，求的最小值．
参考答案与试题解析
一．选择题（共10小题）
1．2024的倒数是
A．2024B．C．D．
【解答】解：2024的倒数是；
故选：．
2．2023年“亚运双节”让杭州火出圈，相关数据显示，国庆期间杭州共接待游客约13000000人次，将数据13000000用科学记数法表示为
A．B．C．D．
【解答】解：，
故选：．
3．第19届亚运会于9月23日至10月8日在杭州成功举办，下列图形中是轴对称图形的是
A．B．
C．D．
【解答】解：、图形不是轴对称图形，不符合题意；
、图形是轴对称图形，符合题意；
、图形不是轴对称图形，不符合题意；
、图形不是轴对称图形，不符合题意．
故选：．
4．如图是我们生活中常用的“空心卷纸”，其主视图为
A．B．C．D．
【解答】解：观察图形可知，该几何体的主视图如下：
．
故选：．
5．“立身以立学为先，立学以读书为本．”为了鼓励全民阅读，某校图书馆开展阅读活动，自阅读活动开展以来，进馆阅读人次逐月增加，第一个月进馆200人次，前三个月累计进馆728人次，若进馆人次的月增长率相同，求进馆人次的月增长率．设进馆人次的月增长率为，依题意可列方程
A．
B．
C．
D．
【解答】解：第一个月进馆200人次，且进馆人次的月增长率为，
第二个月进馆人次，第三个月进馆人次．
根据题意得：．
故选：．
6．下列计算正确的是
A．B．C．D．
【解答】解：．，此选项计算错误，故此选项不符合题意；
．，此选项计算错误，故此选项不符合题意；
．，此选项计算正确，故此选项符合题意；
．，此选项计算错误，故不符合题意；
故选：．
7．对一组数据：4、6、、6、8，描述正确的是
A．中位数是B．平均数是5C．众数是6D．方差是7
【解答】解：对一组数据4、6、、6、8，
将这组数据从小到大排列为，4，6，6，8，最中间的数为6，所以中位数为6，选项描述错误，不符合题意；
其平均数为，选项描述错误，不符合题意；
这组数据中，6出现了2次，出现的次数最多，所以众数为6，选项描述正确，符合题意；
这组数据的方差为，故选项描述错误，不符合题意．
故选：．
8．如图，与位似，点为位似中心，，若的周长是5，则的周长是
A．10B．15C．20D．25
【解答】解：与位似，
，，，
，的周长：的周长，
的周长是5，
的周长是15，
故选：．
9．，两地相距60千米，一艘轮船从地顺流航行至地所用时间比从地逆流航行至地所用时间少45分钟，已知船在静水中航行的速度为20千米时．若设水流速度为千米时，则可列方程为
A．B．
C．D．
【解答】解：根据题意，得：．故选：．
10．如图，在正方形中，是等边三角形，，的延长线分别交于点，，连接，；与相交于点．给出下列结论：①；②；③；④；⑤．其中正确的结论有
A．1个B．2个C．3个D．4个
【解答】解：为等边三角形，
，，
，，
又，，，
，，，
在中，，，
又，，故①正确；
，，，
，故②正确；
，，，
又与同高，，
又，不是中点，，，故③错误；
过点作于，过点作于，
由题意可得，，
，，
，
故④正确，
，，
，，，
又，，，故⑤正确，
综上所述：正确的结论有4个，
故选：．
二．填空题（共5小题）
11．在实数范围内分解因式： ．
【解答】解：．
故答案为：．
12．在平面直角坐标系中，对于平面内任一点，若规定以下三种变换：
①△，，；
②〇，，；
③，，，
按照以上变换例如：△〇，，，则〇等于 ．
【解答】解：〇〇，，．
故答案为：．
13．如图，是反比例函数的图象上一点，过点作轴于点，点在轴上，且，则的值为 ．
【解答】解：设点的坐标为，
点在第二象限，，，
，，
是反比例函数的图象上一点，，
故答案为：．
14．如图，已知，以点为圆心，以任意长为半径画弧，与、分别于点、，再分别以点、为圆心，以大于为半径画弧，两弧相交于点，过上一点作，与相交于点，，则 ．
【解答】解：，，
由题意可知：平分，
．故答案为：．
15．如图，在直角坐标系中，已知点，点为轴正半轴上一动点，连接，以为一边向下作等边，连接，则的最小值为 2 ．
【解答】解：如图，以为对称轴作等边，延长交轴于，
是等边三角形，是等边三角形，
，，，，
，，
，，
，，，
，
，，
，，
点在上移动，
当时，有最小值，
此时，．
故答案为：2．
三．解答题（共7小题）
16．计算：．
【解答】解：原式
．
17．化简求值：，其中为数据4，5，6，5，3，2的众数．
【解答】解：
，
为数据4，5，6，5，3，2的众数，，
当时，原式．
18．某校为了调查本校学生对航空航天知识的知晓情况，开展了航空航天知识竞赛，从参赛学生中，随机抽取若干名学生的成绩进行统计，得到如下不完整的统计图表：
请根据图表信息解答下列问题：
（1）求，，的值；
（2）补全频数分布直方图；
（3）某班有2名男生和1名女生的成绩都为100分，若从这3名学生中随机抽取2名学生参加演讲，用列表或画树状图的方法，求抽取的2名学生恰好为1男1女的概率．
【解答】解：（1）调查人数为：（人，，，，
答：，，；
（2）由各组频数补全频数分布直方图如下：
（3）用树状图法表示所有等可能出现的结果如下：
共有6种等可能出现的结果，其中1男1女的有4种，
所以抽取的2名学生恰好为1男1女的概率是．
19．如图，是的外接圆，直径与交于点，点在的延长线上，连接，．
（1）求证：是的切线；
（2）从以下三个选项中选一个作为条件，使成立，并说明理由；
①；
②；
③；
你选的条件是： ②或③ ．
【解答】（1）证明：是的直径，
，即，
，，
，
，
是的半径，
是的切线；
（2）解：选②或③，
若选②，理由：
，是的直径，
，
由（1）可知，
；
若选③，理由：
，，
又是的直径，，
，．
20．某经销商销售一种成本价为10元的商品，已知销售价不低于成本价，且物价部门规定这种产品的销售价不得高于18元．如图，在销售过程中发现销量与售价（元之间满足一次函数关系．
（1）求与之间的函数关系式，并写出自变量的取值范围；
（2）设销售这种商品每天所获得的利润为元，求与之间的函数关系式，并求出该商品售价定为多少元时，才能使经销商所获利润最大？最大利润是多少？
【解答】解：（1）设关系式为，把，代入得：
，解得：，，
与的之间的函数关系式为，自变量的取值范围为：．
（2），
，抛物线开口向下，对称轴为，在对称轴的左侧，随的增大而增大，
，
当时，（元，
答：与之间的函数关系式为，当该商品销售单价定为18元时，才能使经销商所获利润最大，最大利润是192元．
21．如图1，一灌溉车正为绿化带浇水，喷水口离地竖直高度为米．建立如图2所示的平面直角坐标系，可以把灌溉车喷出水的上、下边缘抽象为两条抛物线的部分图象，把绿化带横截面抽象为矩形，其水平宽度米，竖直高度米，下边缘抛物线是由上边缘抛物线向左平移得到，上边缘抛物线最高点离喷水口的水平距离为2米，高出喷水口0.4米，灌溉车到绿化带的距离为米．
（1）求上边缘抛物线喷出水的最大射程；
（2）求下边缘抛物线与轴交点的坐标；
（3）若米，灌溉车行驶时喷出的水 不能 （填“能”或“不能” 浇灌到整个绿化带，并说明理由．
【解答】解：（1）如图2，由题意得是上边缘抛物线的顶点，
设，
又抛物线过点，
，，
上边缘抛物线的函数解析式为，
当时，，
解得，（舍去），
喷出水的最大射程为；
（2）对称轴为直线，
点的对称点为，
下边缘抛物线是由上边缘抛物线向左平移得到的，
点的坐标为；
（3）不能，理由如下：米，米，米，
点的坐标为，
当时，，
当时，随的增大而减小，
灌溉车行驶时喷出的水不能浇灌到整个绿化带．
22．在矩形中，点是射线上一动点，连接，过点作于点，交直线于点．
（1）当矩形是正方形时，以点为直角顶点在正方形的外部作等腰直角三角形，连接．
①如图1，若点在线段上，则线段与之间的数量关系是 相等 ，位置关系是 ；
②如图2，若点在线段的延长线上，①中的结论还成立吗？如果成立，请给予证明；如果不成立，请说明理由；
（2）如图3，若点在线段上，以和为邻边作平行四边形，是中点，连接，，，求的最小值．
【解答】解：（1）①四边形为正方形，
，，即，
，
，
，又，，
，
，，
为等腰直角三角形，
，，而，
，
四边形为平行四边形，
且，
，，
故答案为：相等；垂直；
②成立，理由是：
当点在线段的延长线上时，
同理可得：，
，，
为等腰直角三角形，
，，而，
，
四边形为平行四边形，
且，
，；
（2）连接，
四边形是平行四边形，，
，，
要最小，即最小，
，，
设，则，
同（1）可得：，
又，
，
，即，，
，
设，当时，取最小值，
的最小值为，
故的最小值为．
成绩分
频数人
频率
10
0.1
15
0.35
40
成绩分
频数人
频率
10
0.1
15
0.35
40