山东省德州市宁津县大曹镇大赵中学2023-2024学年九年级下学期3月份月考检测数学试题（原卷版+解析版）

这是一份山东省德州市宁津县大曹镇大赵中学2023-2024学年九年级下学期3月份月考检测数学试题（原卷版+解析版），文件包含精品解析山东省德州市宁津县大曹镇大赵中学2023-2024学年九年级下学期3月份月考检测数学试题原卷版docx、精品解析山东省德州市宁津县大曹镇大赵中学2023-2024学年九年级下学期3月份月考检测数学试题解析版docx等2份试卷配套教学资源，其中试卷共36页， 欢迎下载使用。
第I卷（选择题共48分）
一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来，每小题选对得4分，选错、不选或选出的答案超过一个均记零分．
1. 的相反数是（ ）
A. B. C. D. 3
【答案】D
【解析】
【分析】此题考查了相反数，利用相反数的定义判断即可．
【详解】的相反数是，
故选：D．
2. 下列运算正确的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据幂的乘方，同底数幂相乘，合并同类项，完全平方公式，即可解答．
【详解】解：，故A 错误；
，故B正确；
，故C错误；
，故D错误．
故选：B．
【点睛】本题考查了幂的乘方，同底数幂相乘，合并同类项，完全平方公式，熟知计算法则是解题的关键．
3. 2023年1月17日，国家航天局公布了我国嫦娥五号月球样品的科研成果．科学家们通过对月球样品的研究，精确测定了月球的年龄是亿年，数据亿年用科学记数法表示为（ ）

A. 年B. 年C. 年D. 年
【答案】B
【解析】
【分析】科学记数法的表现形式为的形式，其中，n为整数，确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，n是正数，当原数绝对值小于1时n是负数；由此进行求解即可得到答案．
【详解】解：亿年年年，
故选B．
【点睛】本题主要考查了科学记数法，解题的关键在于能够熟练掌握科学记数法的定义．
4. 榫卯是古代中国建筑、家具及其它器械的主要结构方式，是我国工艺文化精神的传奇；凸出部分叫榫，凹进部分叫卯，下图是某个部件“卯”的实物图，它的主视图是（ ）

A. B. C. D.
【答案】C
【解析】
【分析】根据主视图是从前向后观察到的图形，进行判断即可．
【详解】解：由题意，得：“卯”的主视图为：

故选C．
【点睛】本题考查三视图，熟练掌握三视图的画法，是解题的关键．
5. 实数，在数轴上对应点的位置如图所示，则下列结论正确的是（ ）

A. B.
C. D.
【答案】D
【解析】
【分析】根据题意可得，然后根据数的乘法和加法法则以及不等式的性质进行判断即可.
【详解】解：由题意可得：，所以，
∴，
观察四个选项可知：只有选项D的结论是正确的；
故选：D.
【点睛】本题考查了实数与数轴以及不等式的性质，正确理解题意、得出是解题的关键.
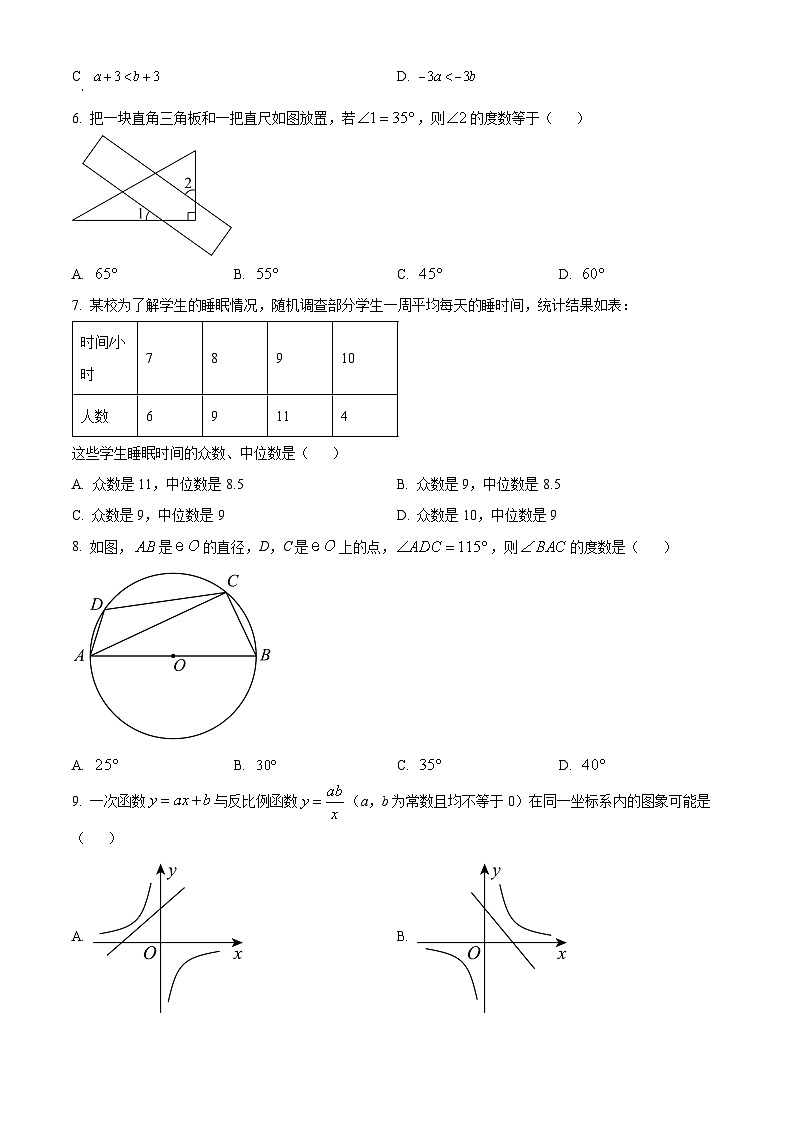
6. 把一块直角三角板和一把直尺如图放置，若，则的度数等于（ ）

A. B. C. D.
【答案】B
【解析】
【分析】如图所示，过点O作，则，由平行线的性质得到，进而推出，由此即可得到答案．
【详解】解：如图所示，过点O作，
∵，
∴，
∴，
∵，
∴，
∵，
∴，
故选B．
【点睛】本题主要考查了平行线的性质与判定，正确作出辅助线是解题的关键．
7. 某校为了解学生的睡眠情况，随机调查部分学生一周平均每天的睡时间，统计结果如表：
这些学生睡眠时间的众数、中位数是（ ）
A. 众数是11，中位数是8.5B. 众数是9，中位数是8.5
C. 众数是9，中位数是9D. 众数是10，中位数是9
【答案】B
【解析】
【分析】根据众数和中位数的定义，即可求解．
【详解】解：睡眠时间为9小时的人数最多，学生睡眠时间的众数是9小时，
一共有30个学生，睡眠时间从小到大排序后，第15、16个数据分别是：8，9，即：中位数为8.5．
故选B．
【点睛】本题主要考查中位数和众数，熟练掌握中位数和众数的定义，是解题的关键．
8. 如图，是的直径，D，C是上的点，，则的度数是（ ）

A. B. C. D.
【答案】A
【解析】
【分析】根据圆内接四边形对角互补和直径所对圆周角等于90度求解即可．
【详解】解：∵，
∴，
∵是的直径，
∴，
∴，
故选：A．
【点睛】本题考查圆的性质，涉及到圆内接四边形对角互补和直径所对圆周角等于90度，熟记知识点是关键．
9. 一次函数与反比例函数（a，b为常数且均不等于0）在同一坐标系内的图象可能是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】先根据一次函数图象确定a、b的符号，进而求出的符号，由此可以确定反比例函数图象所在的象限，看是否一致即可．
【详解】解：A、∵一次函数图象经过第一、二、三象限，
∴，
∴，
∴反比例函数的图象见过第一、三象限，这与图形不符合，故A不符合题意；
B、∵一次函数图象经过第一、二、四象限，
∴，
∴，
∴反比例函数的图象见过第二、四象限，这与图形不符合，故B不符合题意；
C、∵一次函数图象经过第一、三、四象限，
∴，
∴，
∴反比例函数的图象见过第二、四象限，这与图形不符合，故C不符合题意；
D、∵一次函数图象经过第一、二、四象限，
∴，
∴，
∴反比例函数的图象见过第二、四象限，这与图形符合，故D符合题意；
故选D．
【点睛】本题主要考查了一次函数与反比例函数图象和性质，熟练掌握相关性质与函数图象的关系是解决本题的关键．
10. 如图，在中，，，分别以点A、B为圆心，大于的长为半径画弧，两弧分别交于F、G两点，连接F、G分别交于于E、于D，连接，若，则的长为（ ）

A. 6B. C. 9D.
【答案】C
【解析】
【分析】利用基本作图得到垂直平分，则根据线段垂直平分线的性质得到，所以，求出，利用含30度角直角三角形三边的关系求，然后计算即可．
【详解】解：由作法得垂直平分，
∴，
∵，
∴，
∵，
∴，
∴，
在中，，
∴，
∴．
故选：C．
【点睛】本题考查了作图-基本作图：作已知线段的垂直平分线．也考查了线段垂直平分线的性质和含30度角直角三角形的性质．
11. 如图，为等边三角形，点，分别在边，上，，若，，则的长为（ ）

A. B. C. D.
【答案】C
【解析】
【分析】证明，根据题意得出，进而即可求解．
【详解】解：∵为等边三角形，
∴，
∵，，
∴，
∴
∴
∵，
∴，
∴
∵
∴，
故选：C．
【点睛】本题考查了相似三角形的性质与判定，等边三角形的性质，熟练掌握相似三角形的性质与判定是解题的关键．
12. 已知二次函数的部分图象如图所示，图象经过点，其对称轴为直线．下列结论：①；②若点，均在二次函数图象上，则；③关于x的一元二次方程有两个相等的实数根；④满足的x的取值范围为．其中正确结论的个数为（ ）．

A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
【分析】根据抛物线开口向下可得，根据抛物线的对称轴可推得，根据时，，即可得到，推得，故①错误；根据点的坐标和对称轴可得点到对称轴的距离小于点到对称轴的距离，根据抛物线的对称性和增减性可得，故②正确；根据抛物线的图象可知二次函数与直线有两个不同的交点，推得关于x的一元二次方程有两个不相等的实数根，故③错误；根据抛物线的对称性可得二次函数必然经过点，即可得到时，的取值范围，故④正确．
【详解】①∵抛物线开口向下，
∴．
∵抛物线的对称轴为直线，
∴，
由图象可得时，，
即，
而，
∴．故①错误；
②∵抛物线开口向下，抛物线的对称轴为直线．
故当时，随的增大而增大，当时，随的增大而减小，
∵，，
即点到对称轴的距离小于点到对称轴的距离，
故，故②正确；
③由图象可知：二次函数与直线有两个不同的交点，
即关于x的一元二次方程有两个不相等的实数根，故③错误；
④∵函数图象经过，对称轴为直线，
∴二次函数必然经过点，
∴时，的取值范围，故④正确；
综上，②④正确，
故选：B．
【点睛】本题考查了二次函数的性质，二次函数与一元二次方程的关系，二次函数图象与系数的关系：对于二次函数，二次项系数决定抛物线的开口方向和大小，当时，抛物线向上开口；当时，抛物线向下开口；一次项系数和二次项系数共同决定对称轴的位置；常数项决定抛物线与轴交点；熟练掌握二次函数的性质是解题的关键．
第Ⅱ卷（非选择题 共 102 分）
二、填空题：本大题共6小题，共 24分，只要求填写最后结果，每小题填对得4分
13. 分解因式：2x2﹣8=_______
【答案】2（x+2）（x﹣2）
【解析】
【分析】先提公因式，再运用平方差公式．
【详解】2x2﹣8，
=2（x2﹣4），
=2（x+2）（x﹣2）．
【点睛】考核知识点：因式分解.掌握基本方法是关键．
14. 已知关于x的一元二次方程有两个不相等的实数根，则a的取值范围是_______．
【答案】##
【解析】
【分析】利用一元二次方程根的判别式求解即可．
【详解】解：∵关于x的一元二次方程有两个不相等的实数根，
∴，
∴，
故答案为：．
【点睛】本题主要考查了一元二次方程根的判别式，对于一元二次方程，若，则方程有两个不相等的实数根，若，则方程有两个相等的实数根，若，则方程没有实数根．
15. 为了测量一个圆形光盘的半径，小明把直尺、光盘和三角尺按图所示放置于桌面上，并量出，则这张光盘的半径是_______．（精确到．参考数据：）

【答案】
【解析】
【分析】设光盘的圆心为O，三角尺和光盘的切点为C，连接，经过圆外一点A的两条直线都与圆O相切，所以为的角平分线，，同时由切线的性质得到，在中，，求出，即为圆的半径，进而确定出圆的直径．
【详解】解：设光盘圆心为O，三角尺和光盘的切点为C，连接，如下图所示：

∵分别为圆O的切线，
∴为的角平分线，即，
又∵,
∴，
在中，，，
∴，，
∴，
则这张光盘的半径为；
故答案为：．
【点睛】此题考查了切线的性质，切线长定理，锐角三角函数定义，以及特殊角的三角函数值，熟练掌握性质及定理是解本题的关键．
16. 如图，和是以点为位似中心的位似图形．若，则与的面积比是______．

【答案】
【解析】
【分析】本题考查的是位似变换，相似三角形的判定和性质，掌握位似图形的概念、相似三角形的面积比等于相似比的平方是解题的关键．
根据位似变换的性质及相似三角形的面积比等于相似比的平方计算，得到答案．
【详解】解：，
，
和是以点O为位似中心的位似图形，
，，
，
，
，
与的面积比为：，
故答案为：．
17. 如图，在中，，将绕点O旋转至的位置，且是的中点，在反比例函数上，则的值为______．
【答案】
【解析】
【分析】由点是中点，得出，根据旋转得出，再根据30°定理和勾股定理求出点坐标即可．
本题考查了如何确定反比例函数的关系式，利用三角函数求角度及勾股定理的应用是解题关键．
【详解】解：作轴，
∵是的中点，
∴
∴，
∴，
∴，
∵绕点O旋转至的位置，
∴，
∴
∴
∵，
∴
∴，
∴
故答案为：．
18. 如图1，在中，动点P从点A出发沿折线匀速运动至点A后停止．设点P的运动路程为x，线段的长度为y，图2是y与x的函数关系的大致图象，其中点F为曲线的最低点，则的高的长为______．
【答案】
【解析】
【分析】本题考查了动点问题函数图象，勾股定理，垂线段最短，从函数图象获取信息是解题的关键．
过点A作于点Q，当点P与Q重合时，在图2中F点表示当时，点P到达点Q，此时当P在上运动时，最小，勾股定理求得．然后等面积法即可求解．
【详解】解：如图过点A作于点Q，当点P与Q重合时，在图2中F点表示当时，点P到达点Q，此时当P在上运动时，最小，
，，，
在中，，，
，
，
故答案为：.
三、解答题：本大题共7小题，共 78 分．解答要写出必要的文字说明、证明过程或演算步骤
19. （1）化简：；
（2）解不等式组：．
【答案】（1）；（2）
【解析】
【分析】（1）根据分式的混合计算法则求解即可；
（2）先求出每个不等式的解集，再根据 “同大取大，同小取小，大小小大中间找，大大小小找不到（无解）”求出不等式组的解集即可．
【详解】解：（1）
；
（2）
解不等式①得：，
解不等式②得：，
∴不等式组的解集为
【点睛】本题主要考查了分式的混合计算，解一元一次不等式组，正确计算是解题的关键．
20. 为了解学生的课外阅读情况，七（1）班针对“你最喜爱的课外阅读书目”进行调查（每名学生必须选一类且只能选一类阅读书目），并根据调查结果列出统计表，绘制成扇形统计图．
男、女生所选类别人数统计表
根据以上信息解决下列问题
（1） ， ；
（2）扇形统计图中“科学类”所对应扇形圆心角度数为 ；
（3）从选哲学类的学生中，随机选取两名学生参加学校团委组织的辩论赛，请用树状图或列表法求出所选取的两名学生都是男生的概率．
【答案】（1）10，2（2）79.2（3）
【解析】
【分析】（1）根据文学类的人数和所占的百分比求出抽查的总人数，再根据各自所占的百分比即可求出、；
（2）由乘以“科学类”所占的比例，即可得出结果；
（3）根据题意画出树状图得出所有等情况数和所选取的两名学生都是男生的情况数，然后根据概率公式即可得出答案．
【详解】（1）抽查的总学生数是：（人），
，；
故答案为10，2；
（2）扇形统计图中“科学类”所对应扇形圆心角度数为；
故答案为79.2；
（3）列表得：
由表格可知，共有12种可能出现的结果，并且它们都是等可能的，其中所选取的两名学生都是男生的有2种可能，
∴所选取的两名学生都是男生的概率为.
【点睛】此题主要考查了列表法与树状图法，以及扇形统计图、统计表的应用，解题关键在于看懂图中数据．
21. 图1是某越野车的侧面示意图，折线段表示车后盖，已知，，，该车的高度．如图2，打开后备箱，车后盖落在处，与水平面的夹角．

（1）求打开后备箱后，车后盖最高点到地面的距离；
（2）若小琳爸爸的身高为，他从打开的车后盖处经过，有没有碰头的危险?请说明理由．
（结果精确到，参考数据：，，，）
【答案】（1）车后盖最高点到地面的距离为
（2）没有危险,详见解析
【解析】
【分析】（1）作，垂足为点，先求出的长，再求出的长即可；
（2）过作，垂足为点，先求得，再得到，再求得，从而得出到地面的距离为，最后比较即可．
【小问1详解】
如图，作，垂足为点

在中
∵，
∴
∴
∵平行线间的距离处处相等
∴
答：车后盖最高点到地面的距离为．
【小问2详解】
没有危险，理由如下：
过作，垂足为点

∵，
∴
∵
∴
在中，
∴．
∵平行线间的距离处处相等
∴到地面的距离为．
∵
∴没有危险．
【点睛】本题主要考查了解直角三角形的应用，掌握直角三角形的边角关系是解题的关键．
22. 某校开设智能机器人编程的校本课程，购买了A，B两种型号的机器人模型．A型机器人模型单价比B型机器人模型单价多200元，用2000元购买A型机器人模型和用1200元购买B型机器人模型的数量相同．
（1）求A型，B型机器人模型的单价分别是多少元?
（2）学校准备再次购买A型和B型机器人模型共40台，购买B型机器人模型不超过A型机器人模型的3倍，且商家给出了两种型号机器人模型均打八折的优惠．问购买A型和B型机器人模型各多少台时花费最少?最少花费是多少元?
【答案】（1）A型编程机器人模型单价是500元，B型编程机器人模型单价是300元
（2）购买A型机器人模型10台和B型机器人模型30台时花费最少，最少花费是11200元
【解析】
【分析】（1）设A型编程机器人模型单价是元，B型编程机器人模型单价是元，根据：用2000元购买A型机器人模型和用1200元购买B型机器人模型的数量相同即可列出关于x的分式方程，解方程并检验后即可求解；
（2）设购买A型编程机器人模型台，购买A型和B型编程机器人模型共花费元，根据题意可求出m的范围和W关于m的函数关系式，再结合一次函数的性质即可求出最小值
【小问1详解】
解：设A型编程机器人模型单价是元，B型编程机器人模型单价是元．
根据题意，得
解这个方程，得
经检验，是原方程的根．
答：A型编程机器人模型单价是500元，B型编程机器人模型单价是300元．
【小问2详解】
设购买A型编程机器人模型台，购买B型编程机器人模型台，购买A型和B型编程机器人模型共花费元，
由题意得：，解得．
∴
即，
∵，
∴随的增大而增大．
∴当时，取得最小值11200，此时；
答：购买A型机器人模型10台和B型机器人模型30台时花费最少，最少花费是11200元．
【点睛】本题考查了分式方程的应用、一元一次不等式的应用和一次函数的性质，正确理解题意、找准相等与不等关系、得出分式方程与不等式是解题的关键．
23. 如图，内接于，，点E在直径CD的延长线上，且．
（1）试判断AE与的位置关系，并说明理由；
（2）若，求阴影部分面积．
【答案】（1）AE与⊙O相切，理由见详解；（2）．
【解析】
【分析】（1）利用圆周角定理以及等腰三角形的性质得出∠E=∠ACE=∠OCA=∠OAC=30°，∠EAC=120°，进而得出∠EAO=90°，即可得出答案；
（2）连接AD，利用解直角三角形求出圆的半径，然后根据，即可求出阴影部分的面积．
【详解】（1）AE与⊙O相切，理由如下：
连接AO，
∵∠B=60°，
∴∠AOC=120°，
∵AO=CO，AE=AC，
∴∠E=∠ACE，∠OCA=∠OAC=30°，
∴∠E=∠ACE=∠OCA=∠OAC=30°，
∴∠EAC=120°，
∴∠EAO=90°，
∴AE是⊙O的切线；
（2）连接AD，则，
∴∠DAC=90°，
∴CD为⊙O的直径，
在Rt△ACD中，AC=6，∠OCA=30°，
∴，
∴，
∴，∠AOD=60°，
∴
∴．
【点睛】本题考查了圆的切线的判定和性质，解直角三角形，圆周角定理，等腰三角形的判定和性质，解题的关键是熟练掌握所学的知识，正确作出辅助线，从而进行解题．
24. （1）用数学的眼光观察．
如图，在四边形中，，是对角线的中点，是的中点，是的中点，求证：．
（2）用数学的思维思考．
如图，延长图中的线段交的延长线于点，延长线段交的延长线于点，求证：．
（3）用数学的语言表达．
如图，在中，，点在上，，是的中点，是的中点，连接并延长，与的延长线交于点，连接，若，试判断的形状，并进行证明．
【答案】（1）见解析；（2）见解析；（3）是直角三角形，证明见解析．
【解析】
【分析】（1）根据中位线定理即可求出，利用等腰三角形的性质即可证明；
（2）根据中位线定理即可求出和，通过第（1）问的结果进行等量代换即可证明；
（3）根据中位线定理推出和从而求出，证明是等边三角形，利用中点求出，从而求出度数，即可求证的形状.
【详解】证明：（1）的中点，是的中点，
.
同理，.
，
.
.
（2）的中点，是的中点，
，
.
同理，.
由（1）可知，
（3）是直角三角形，证明如下：
如图，取的中点，连接，，
是的中点，
，.
同理，，.
，
.
.
，
，
.
，
.
又，
是等边三角形，
.
又，
.
，
.
是直角三角形.
故答案为：是直角三角形.
【点睛】本题考查了三角形的中位线定理，等腰三角形的性质，等边三角形的性质以及直角三角形的判定，解题的关键在于灵活运用中位线定理.
25. 已知抛物线与轴相交于点，，与轴相交于点．
（1）求抛物线的表达式；
（2）如图1，点是抛物线的对称轴上的一个动点，当的周长最小时，求的值；
（3）如图2，取线段的中点，在抛物线上是否存在点，使？若存在，求出点的坐标；若不存在，请说明理由．
【答案】（1）
（2）
（3）或或或
【解析】
【分析】（1）待定系数法求函数解析式即可；
（2）根据的周长等于，以及为定长，得到当的值最小时，的周长最小，根据抛物线的对称性，得到关于对称轴对称，则：，得到当三点共线时，，进而求出点坐标，即可得解；
（3）求出点坐标为，进而得到，得到，分点在点上方和下方，两种情况进行讨论求解即可．
【小问1详解】
解：∵抛物线与轴相交于点，，
∴，解得：，
∴；
【小问2详解】
∵，当时，，
∴，抛物线的对称轴为直线
∵的周长等于，为定长，
∴当的值最小时，的周长最小，
∵关于对称轴对称，
∴，当三点共线时，的值最小，为的长，此时点为直线与对称轴的交点，
设直线的解析式为：，
则：，解得：，
∴，
当时，，
∴，
∵，
∴，，
∴；
【小问3详解】
解：存在，
∵为的中点，
∴，
∴，
∵，
∴，
在中，，
∵，
∴，
①当点在点上方时：
过点作，交抛物线与点，则：，此时点纵坐标为2，
设点横坐标，
则：，
解得：，
∴或；
②当点在点下方时：设与轴交于点，
则：，
设，
则：，，
∴，解得：，
∴，
设的解析式为：，
则：，解得：，
∴，
联立，解得：或，
∴或；
综上：或或或．
【点睛】本题考查二次函数的综合应用，正确的求出二次函数解析式，利用数形结合，分类讨论的思想进行求解，是解题的关键．本题的综合性强，难度较大，属于中考压轴题．
时间/小时
7
8
9
10
人数
6
9
11
4
类别
男生（人）
女生（人）
文学类
12
8
史学类
5
科学类
6
5
哲学类
2
男1
男2
女1
女2
男1
﹣﹣
男2男1
女1男1
女2男1
男2
男1男2
﹣﹣
女1男2
女2男2
女1
男1女1
男2女1
﹣﹣
女2女1
女2
男1女2
男2女2
女1女2
﹣﹣