

湖北省襄阳市宜城市2022-2023学年七年级下学期期末学业质量监测数学试卷(答案不全)
展开一、选择题(本大题有10个小题,每小题3分,共30分),在每小题给出的四个选项中,只有一项是符合题意的,请将其标号在答题卡上涂黑作答.
1.下面四个数中最大的数是( )
A.1B.C.0D.π
2.下列计算正确的是( )
A.B.C.D.
3.在平面直角坐标系中,点B在第二象限,并且到x轴和y轴的距离分别是3和2,则点B坐标为( )
A.(3,-2)B.(2,-3)C.(-2,3)D.(-3,2)
4.下面统计调查中,适合采用全面调查的是( )
A.调查市场上某食品防腐剂是否符合国家标准B.对某品牌手机的防水性能的调查
C.疫情期间对国外入境人员的核酸检测D.调查我市初中生每周“诵读经典”的时间
5.如果,那么x,y的值为( )
A.B.C.D.
6.已知,下列不等式一定成立的是( )
A.B.C.D.
7.《九章算术》是中国古代第一部数学专著,也是世界上最早的印刷本数学书,它的出现标志着中国古代数学体系的形成.书中有如下问题:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?大意是:有几个人一起去买一件物品,如果每人出8元,则多了3元;如果每人出7元,则少了4元,问有多少人?该物品价值多少元?若设有x人,物品价值y元,根据题意,可列方程组为( )
A.B.C.D.
8.不等式组的解集在数轴上表示为( )
A.B.C.D.
9.如图,BC∥DE,且∠CDE=70°,若要使AB∥CD,则∠ABC的度数为( )
A.90°B.100°C.110°D.120°
10.如图,将对边平行的纸带折叠,若∠1+∠2=100°,则∠3的度数是( )
A.65°B.64°C.62°D.60°
二、填空题(本大题共6个小题,每小题3分,共18分)把答案填在答题卡的相应位置上.
11.的绝对值______.
12.在一个样本容量为80的样本所绘制的频数分布直方图中,第一、二、三、四小组所对应的各个长方形高的比为2:3:4:1,那么第三组的频数是______.
13.当a______时,不等式的解集是.
14.已知关于x,y的方程组,若x+y=5,则k的值为______.
15.在平面直角坐标系中,点,,且直线AB∥x轴,则m的值是______.
16.如图,三角形ABC的面积为10,∠ACB=90°,把三角形ABC沿BC方向平移至三角形DEF的位置,平移距离是BC长的2倍,则四边形ABED的面积为______.
三、解答题(本大题共9个小题,共72分)解答应写出文字说明,证明过程或验算步骤,并且写在答题卡上每题对应的答题区域内.
17.(本小题满分6分)计算及解方程组:
(1)
(2)
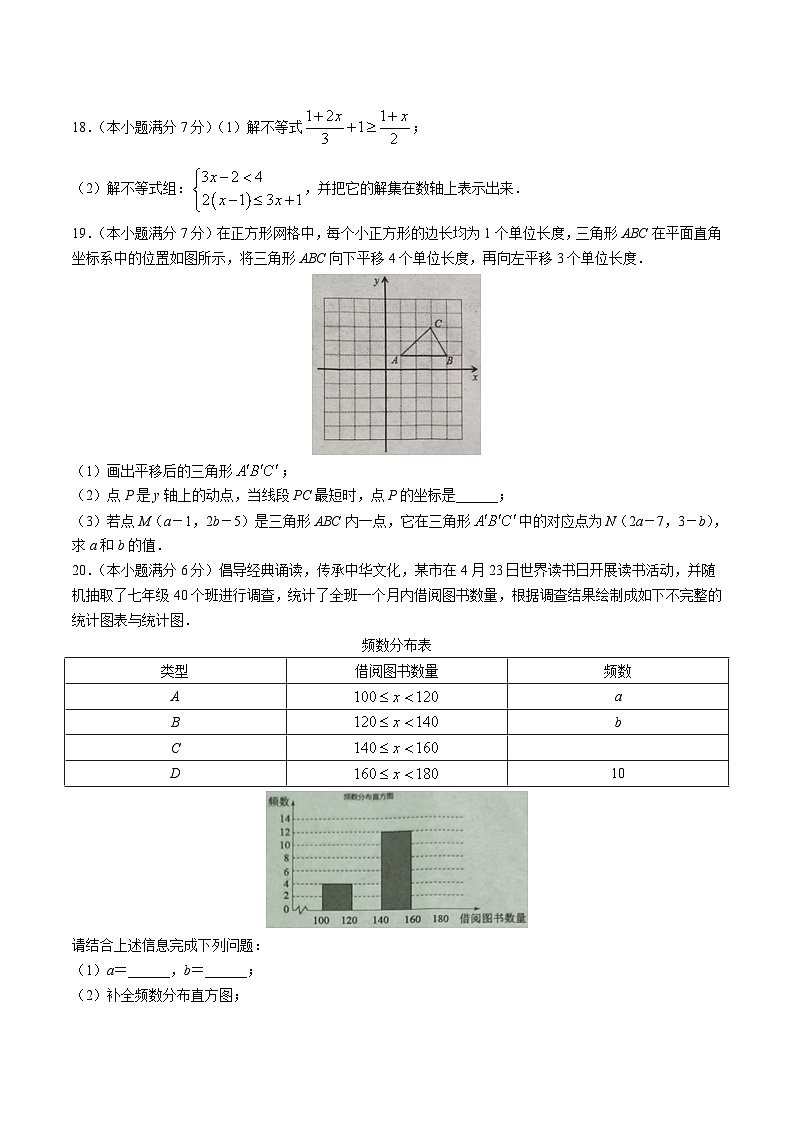
18.(本小题满分7分)(1)解不等式;
(2)解不等式组:,并把它的解集在数轴上表示出来.
19.(本小题满分7分)在正方形网格中,每个小正方形的边长均为1个单位长度,三角形ABC在平面直角坐标系中的位置如图所示,将三角形ABC向下平移4个单位长度,再向左平移3个单位长度.
(1)画出平移后的三角形;
(2)点P是y轴上的动点,当线段PC最短时,点P的坐标是______;
(3)若点M(a-1,2b-5)是三角形ABC内一点,它在三角形中的对应点为N(2a-7,3-b),求a和b的值.
20.(本小题满分6分)倡导经典诵读,传承中华文化,某市在4月23日世界读书日开展读书活动,并随机抽取了七年级40个班进行调查,统计了全班一个月内借阅图书数量,根据调查结果绘制成如下不完整的统计图表与统计图.
频数分布表
请结合上述信息完成下列问题:
(1)a=______,b=______;
(2)补全频数分布直方图;
(3)该市要对借阅图书数量达到优秀(不低于140本)的班级进行表彰,按借阅图书数量从高到低设一、二、三等奖,并且一、二、三等奖的班级比例为1:3:6,若该市七年级有600个班,根据抽样调查结果,请估计该市获得二等奖的班级有多少个.
21.(本小题满分6分)老张与老李购买了相同数量的种兔,一年后,老张养兔数比买入种兔数增加了2只,老李养兔数比买入种兔数的2倍少1只,老张养兔数不超过老李养兔数的.一年前老张至少买了多少只种兔?
22.(本小题满分7分)某校组织七年级学生到青少年实践活动基地研学旅行,已知用4辆小客车和1辆大客车每次可运送学生125人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若该校七年级共有300名学生,请直接写出每辆车都坐满的租车方案.
23.(本小题满分10分)(1)【问题】如图1,若AB∥CD,∠BEP=25°,∠PFD=30°.则∠EPF=______;
(2)【问题归纳】如图1,若AB∥CD,请猜想∠BEP,∠PFD,∠EPF之间有何数量关系?请说明理由;
(3)【联想拓展】如图2,AB∥CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?直接写出结论.
24.(本小题满分11分)某服装店准备采购甲、乙两种不同品牌的防晒服,已知2件甲种防晒服和1件乙种防晒服共需要550元,3件甲种防晒服和2件乙种防晒服共需要900元.
(1)甲、乙两种防晒服每件分别是多少元?
(2)该服装店准备用不超过3500元的资金采购甲、乙两种防晒服共20件,其中购进甲种防晒服的件数不少于8件,采购的件数须为整数,那么该服装店有哪几种采购方案?
(3)在(2)的条件下,已知该服装店销售甲种防晒服1件可获利3m(m>0)元,销售乙种防晒服1件可获利4m元,若20件服装全部售出的最大利润为792元,请直接写出m的值______.
25.(本小题满分12分)在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且满足,现同时将点A,B分别向上平移4个单位长度,再向右平移3个单位长度,分别得到点A,B的对应点D,C,连接AD,BC,CD.
(1)求点C,D的坐标.
(2)求四边形ABCD的面积.
(3)在y轴上是否存在点P,使三角形PAB的面积等于四边形ABCD的面积?若存在,请求出点P的坐标;若不存在,请说明理由.
2022-2023学年度下学期期末考试题
七 年 级 数 学评分标准
一、选择题 (本大题有10个小题,在下面的每小题的四个选项中,有且只有一个符合题意,把符合题意的选项代号填在题后括号内,每小题3分,共30分.)
BDCCABABCA
二、填空题(把各题的正确答案填在题后的横线上,每小题3分,共18分.)
11.() 12.(32) 13.(a<1)
14. (4) 15. (±3) 16.(40)
三、解答题(本题有9个小题,共72分.)
17.(本题满分6分)
解:(1)原式.…………………3分
(2),
①+②×3得:10x=50,解得:x=5,
把x=5代入②得:10+y=13,解得:y=3,
则方程组的解为.…………………6分
18.(本题满分7分)
解:(1)去分母得:2(1+2x)+6≥3(1+x),
去括号得:2+4x+6≥3+3x,
移项得:4x﹣3x≥3﹣2﹣6,
合并得:x≥﹣5.…………………3分
(2),
解不等式①,得x<2,
解不等式②,得x≥﹣3,
不等式①,不等式②的解集在数轴上表示,如图:
,
则原不等式组的解集为﹣3≤x<2.…………………7分
19.(本题满分7分)
解:(1)图略;…………………2分
(2)(0,3);…………………2分
(3)由题意得,
解之得.…………………7分
20.(本题满分6分)
解:(1)4,14.…………………2分
(2)补全图形如下:…4分
(3)借阅图书数量达到优秀(不低于140本)的班级的对应百分比为(12+10)÷40×100%=55%,
估计该市获得表彰的班级数为600×55%=330(个).
所以该市获得二等奖的班级有(个).…………………6分
21.(本题满分6分)
解:设一年前老张买了x只种兔,则
.…………………3分
解得:x≥8.
答:一年前老张至少买了8只种兔.…………………6分
22.(本题满分7分)
解:(1)设每辆小客车能坐x名学生,每辆大客车能坐y名学生,
依题意得:,
解得:.
答:每辆小客车能坐20名学生,每辆大客车能坐45名学生.…………………4分
(2)方案1:15辆小客车;方案2:6辆小客车和4辆大客车. …………………7分
23.(本题满分10分)
解:(1)55°;…………………3分
(2)∠BEP+∠PFD=∠EPF,理由如下:
过点P作PM∥AB,
∵AB∥CD,
∴AB∥CD∥PM.
∴∠BEP=∠EPM,∠PFD=∠FPM.
∴∠EPF=∠EPM+∠FPM=∠BEP+∠PFD.…………………7分
(3)∠PFC=∠PEA+∠EPF.…………………10分
24.(本题满分11分)
解:(1)设甲种防晒服每件是x元、乙种防晒服每件是y元,
根据题意得:,
解得,
答:甲种防晒服每件是200元、乙种防晒服每件是150元;…………………4分
(2)设购买甲种防晒服a件,则购买乙种防晒服(20-a)件,
根据题意得:,且a≥10,
解得8≤a≤10,
∵a为整数,
∴a=8,9,10,
故该服装店有3种采购方案,
方案一:购买甲种防晒服8件,乙种防晒服12件;
方案二:购买甲种防晒服9件,乙种防晒服11件;
方案三:购买甲种防晒服10件,乙种防晒服10件.…………………8分
(3)设防晒服全部售出的利润为w元,根据题意得:
w=3m(20-a)+4ma=ma+60m,
∵m>0,∴w随a的增大而增大,
∴a=12时w有最大值,
即12m+60m=792,解得m=11.…………………11分
25.(本题满分12分)
解:(1)∵,∴a+3=0,b﹣4=0.
∴a=﹣3,b=4.
∴A(﹣3,0),B(4,0).
∴C(7,4),D(0,4).…………………4分
(2)∵A(﹣3,0),B(4,0),C(7,4),D(0,4),
∴AB=7,OD=4.
∴S四边形ABCD=AB•OD=7×4=28.…………………8分
(3)y轴上存在点P,使三角形PAB的面积等于四边形ABCD的面积.
设点P的坐标为(0,y),
则.
∴解得y=±8.
∴当点P的坐标为(0,8)或(0,﹣8),三角形PAB的面积等于四边形ABCD的面积.
…………………12分
类型
借阅图书数量
频数
A
a
B
b
C
D
10
湖北省襄阳市宜城市2022-2023学年八年级下学期期末学业质量测试数学试卷(含答案): 这是一份湖北省襄阳市宜城市2022-2023学年八年级下学期期末学业质量测试数学试卷(含答案),共11页。
湖北省襄阳市襄阳五中学实验中学2022-2023学年数学七下期末学业质量监测试题含答案: 这是一份湖北省襄阳市襄阳五中学实验中学2022-2023学年数学七下期末学业质量监测试题含答案,共7页。
2022-2023学年湖北省襄阳市宜城区数学七年级第二学期期末学业质量监测模拟试题含答案: 这是一份2022-2023学年湖北省襄阳市宜城区数学七年级第二学期期末学业质量监测模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,在平面直角坐标系中,已知点A,下列计算正确的是等内容,欢迎下载使用。












