高中数学人教A版 (2019)选择性必修 第一册1.1 空间向量及其运算课前预习课件ppt

这是一份高中数学人教A版 (2019)选择性必修 第一册1.1 空间向量及其运算课前预习课件ppt，共34页。PPT课件主要包含了a·b＝0，λa·b，b·a，a·c＋b·c，答案A等内容，欢迎下载使用。

(一)教材梳理填空1．空间向量的夹角
2．空间向量的数量积(1)定义：已知两个非零向量a，b，则 叫做a，b的数量积，记作a·b. 即a·b＝ ．[微提醒]　零向量与任意向量的数量积为0.(2)由数量积的定义，可以得到：a⊥b⇔ ；a·a＝|a||a|cs〈a，a〉＝ .
|a||b|cs〈a，b〉
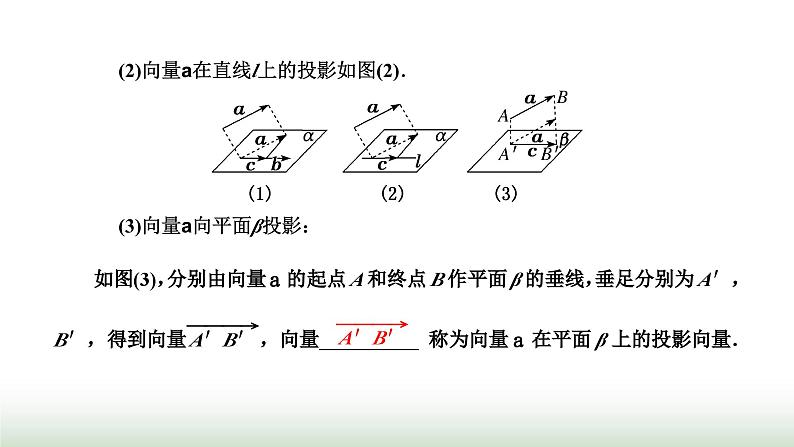
(2)向量a在直线l上的投影如图(2)．(3)向量a向平面β投影：
4．空间向量数量积的运算律(1)(λa)·b＝ ，λ∈R；(2)a·b＝ (交换律)；(3)(a＋b)·c＝ (分配律)．[微提醒]　(1)两个向量的数量积是数量，而不是向量，它可以是正数、负数或零；(2)向量数量积的运算不满足消去律和乘法的结合律，即a·b＝a·c⇒b＝c，(a·b)·c＝a·(b·c)都不成立．
(2)若a·b＝0，则a＝0或b＝0.(　　 )(3)对于非零向量a，b，〈a，b〉与〈a，－b〉相等．(　　)(4)若a·b＝b·c，且b≠0，则a＝c.(　　)(5)若a，b均为非零向量，则a·b＝|a||b|是a与b共线的充要条件．(　　 )答案：(1)×　(2)×　(3)×　(4)×　(5)×
求空间向量数量积的步骤(1)将各向量分解成已知模和夹角的向量的组合形式；(2)利用向量的运算律将数量积展开，转化为已知模和夹角的向量的数量积；(3)代入a·b＝|a||b|cs〈a，b〉求解．　　
[对点练清]1．已知a＝3p－2q，b＝p＋q，p和q是相互垂直的单位向量，则a·b＝(　　 )A．1　　B．2　　　C．3　　D．4解析：∵p⊥q且|p|＝|q|＝1，∴a·b＝(3p－2q)·(p＋q)＝3p2＋p·q－2q2＝3＋0－2＝1.答案：A　
题型二　利用数量积求模及夹角 [学透用活][典例2]　如图所示，P为△ABC所在平面外一点，PA＝PB＝PC＝1，∠APB＝∠BPC＝60°，∠APC＝90°，若G为△ABC的重心，则PG的长为______，异面直线PA与BC所成角的余弦值为____．
[提醒]　求向量夹角，必须特别关注两向量的方向，注意向量夹角与异面直线所成角的区别．　　
[对点练清]1.如图，BB1⊥平面ABC，且△ABC是∠B＝90°的等腰直角三角形，▱ABB1A1，▱BB1C1C的对角线都分别相互垂直且相等，若AB＝a，求异面直线BA1与AC所成的角．
2．已知线段AB在平面α内，线段AC⊥α，线段BD⊥AB，且与α所成的角是30°，如果AB＝a，AC＝BD＝b，求C，D间的距离．
题型三　利用向量数量积判断或证明垂直问题 [学透用活][典例3]　如图所示，在四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB＝60°，AB＝2AD，PD⊥底面ABCD.求证：PA⊥BD.
利用向量数量积判断或证明线线、线面垂直的思路(1)由数量积的性质a⊥b⇔a·b＝0(a，b≠0)可知，要证两直线垂直，可分别构造与两直线平行的向量，只要证明这两个向量的数量积为0即可．(2)用向量法证明线面垂直，离不开线面垂直的判定定理，需将线面垂直转化为线线垂直，然后利用向量法证明线线垂直即可．　　
[对点练清]如图，在正方体ABCD-A1B1C1D1中，E，F，G分别是棱CC1，BC，CD的中点．求证：A1G⊥平面DEF.