【中考二轮】2024年中考数学【热点·重点·难点】（安徽专用）安徽省中考数学模拟卷（一）-专题训练.zip

这是一份【中考二轮】2024年中考数学【热点·重点·难点】（安徽专用）安徽省中考数学模拟卷（一）-专题训练.zip，文件包含2024年安徽省中考数学模拟卷一原卷版docx、2024年安徽省中考数学模拟卷一解析版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。
一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A，B，C，D四个选项，其中只有一个是符合题目要求的.
1．已知与互为相反数，且，那么下列关系式正确的是
A．B．C．D．
2．如图为某几何体的三种视图，这个几何体可以是
A．B．C．D．
3．下列运算正确的是
A．B．C．D．
4．不等式的解集在数轴上表示为
A．B．
C．D．
5．下列函数中，的值随值的增大而减小的是
A．B．C．D．
6．如图，正五边形内接于，点是 上的动点，则的度数为
A．B．
C．D．随着点的变化而变化
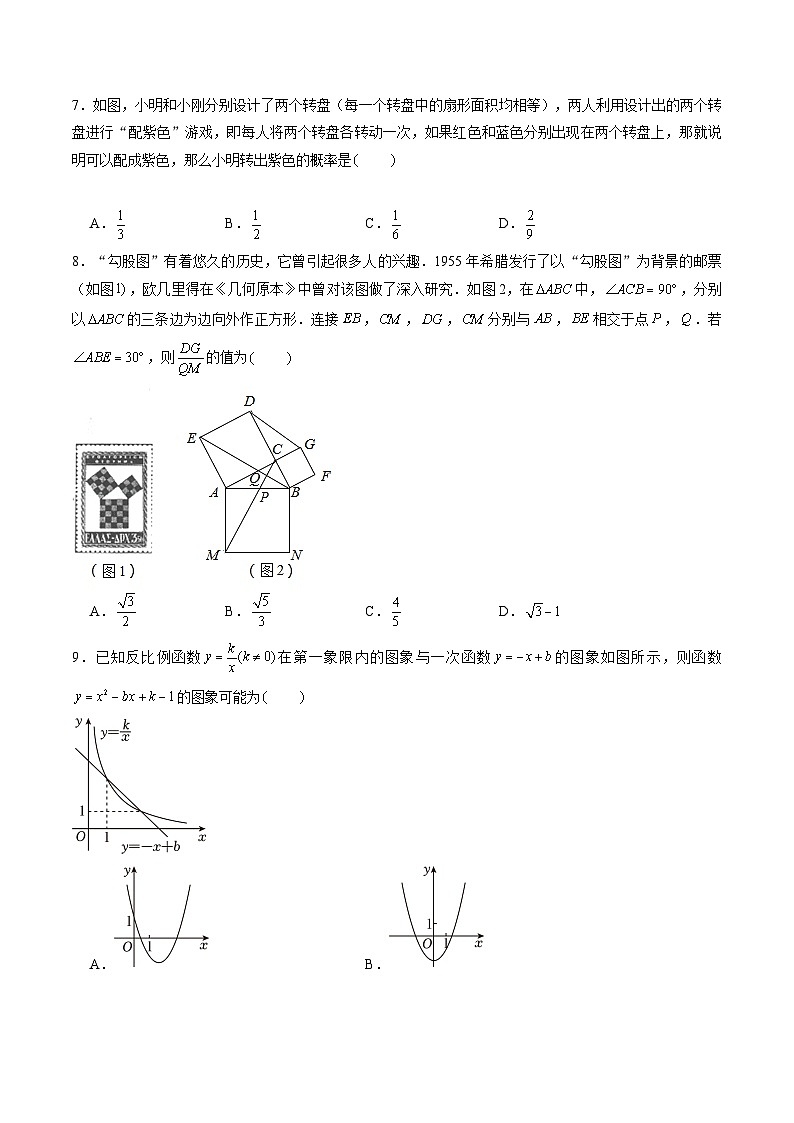
7．如图，小明和小刚分别设计了两个转盘（每一个转盘中的扇形面积均相等），两人利用设计出的两个转盘进行“配紫色”游戏，即每人将两个转盘各转动一次，如果红色和蓝色分别出现在两个转盘上，那就说明可以配成紫色，那么小明转出紫色的概率是
A．B．C．D．
8．“勾股图”有着悠久的历史，它曾引起很多人的兴趣．1955年希腊发行了以“勾股图”为背景的邮票（如图，欧几里得在《几何原本》中曾对该图做了深入研究．如图2，在中，，分别以的三条边为边向外作正方形．连接，，，分别与，相交于点，．若，则的值为
A．B．C．D．
9．已知反比例函数在第一象限内的图象与一次函数的图象如图所示，则函数的图象可能为
A．B．
C．D．
10．如图，等边边长为，、分别是边、上两个动点且．分别连接、，交于点，点为的中点，为上一动点，则的最小值为
A．B．C．D．4
二、填空题（本大题共4小题，每小题5分，满分20分）
11．计算： ．
12．过度包装既浪费资源又污染环境，据测算，如果全国每年减少的过度包装纸用量，那么可减排二氧化碳4280000吨．把数4280000用科学记数法表示为 ．
13．如图，是斜边上的中线．，，点是上一个动点，过点分别作和的垂线，垂足为、．则的值是 ．
14．如图，点在直线上，轴于点，点在线段上，以为边作正方形，点恰好在反比例函数为常数，第一象限的图象上，连接．
（1）若，，则 ；
（2）若，则 ．
三、（本大题共2小题，每小题8分，满分16分）
15．先化简，再求值：，其中．
16．2024年元旦，驿城区某校勤工俭学小组为筹集养老院春节文艺汇演费用，他们用274元钱从蔬菜批发市场批发了西红柿和豆角共到菜市场去卖，西红柿和豆角这天的批发价与零售价如表所示：
则他们当天卖完这些西红柿和豆角能赚到多少钱可用于汇演费用？
四、（本大题共2小题，每小题8分，满分16分）
17．如图，在边长为1个单位长度的小正方形网格中，给出了（顶点是网格线的交点）和直线．
（1）在直线上找一点，使点到边，的距离相等；
（2）画出关于直线对称的图形△；再将△向下平移4个单位长度，画出平移后得到的图形△；
（3）结合轴对称变换和平移变换的有关性质，两个对应图形和△的对应点所具有的性质是 ．
．对应点连线互相平行
．对应点连线被直线垂直平分
．对应点连线被直线平分或与直线重合
18．丰艳花卉市场将深色和浅色两种花齐摆成如图所示的排列图案，第1个图案需要5盆花卉，第2个图案需要13盆花卉，第3个图案需要25盆花卉，以此类推．
按照以上规律，解决下列问题：
（1）第4个图案需要花卉 盆；
（2）第个图案需要花卉 盆（用含的代数式表示）；
（3）已知丰艳花卉市场春节期间所摆的花卉图案中深色花卉比浅色花卉多101盆，求该花卉图案中深色花卉的盆数．
五、（本大题共2小题，每小题10分，满分20分）
19．如图，塔前有一高为的观景台，已知，，点，，在同一条水平直线上．某学习小组在观景台处测得塔顶部的仰角为，在观景台处测得塔顶部的仰角为．求塔的高度，，结果取整数）．
20．阅读下列相关材料，并完成相应的任务．
任务：
（1）请你完成这个定理的证明过程．
（2）该数学兴趣小组的同学在该定理的基础上写出了另外一个命题：若圆内接四边形的对角线互相垂直，则一边中点与对角线交点的连线垂直于对边请判断此命题是 命题．（填“真”或“假”
（3）若，，，求的长．
六、（本题满分12分）
21．甲、乙、丙三个家电厂家在广告中都声称，他们的某种电子产品在正常情况下的使用寿命都是8年，经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查，统计结果如下：（单位：年）
甲厂：4，5，5，5，5，7，9，12，13，15；
乙厂：6，6，8，8，8，9，10，12，14，15；
丙厂：4，4，4，6，7.9，13，15，16，16；
根据以上数据，绘制了下面不完整的表格：
根据以上信息解答下列问题：
（1）表格中 ， ；
（2）这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数？
（3）如果这三个家电厂家的电子产品的售价相同，则顾客购买哪一家的电子产品更合适，并说明理由．
七、（本题满分12分）
22．如图，抛物线经过，两点，并交轴于另一点，点是抛物线的顶点，直线与轴交于点．
（1）求该抛物线的表达式；
（2）若点是轴上一动点，分别连接，，求的最小值；
（3）若点是抛物线上一动点，问在对称轴上是否存在点，使得以，，，为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点的坐标；若不存在，请说明理由．
八、（本题满分14分）
23．如图，已知矩形中，，，点是边的中点，点是矩形内一个动点，且．
（1）当时，连接、，直接写出的度数；
（2）当时，连接，若，求的长；
（3）当时，将线段绕点逆时针旋转后，得到线段，点是线段的中点，当点在矩形内部运动时，求点运动路径的长度．
品名
西红柿
豆角
批发价（单位：元
6.2
7.2
零售价（单位：元
7.8
9
布拉美古塔定理
婆罗摩笈多是古印度著名的数学家、天文学家，他编著了《婆罗摩修正体系》，他曾经提出了“婆罗摩笈多定理”，也称“布拉美古塔定理”．定理的内容是：若圆内接四边形的对角线互相垂直，则垂直于一边且过对角线交点的直线平分对边．
某数学兴趣小组的同学写出了这个定理的已知和求证．
已知：如图，在圆内接四边形中，对角线，垂足为，过点作的垂线分别交，于点，．
求证：是的中点
平均数
众数
中位数
甲厂
8
5
6
乙厂
9.6
8.5
丙厂
9.4
4