【中考二轮】2024年中考数学【热点·重点·难点】（安徽专用）热点03一次函数与反比例函数（8种考向+重难通关练+培优争分练）-专题训练.zip

这是一份【中考二轮】2024年中考数学【热点·重点·难点】（安徽专用）热点03一次函数与反比例函数（8种考向+重难通关练+培优争分练）-专题训练.zip，文件包含热点03一次函数与反比例函数8种考向+重难通关练+培优争分练原卷版docx、热点03一次函数与反比例函数8种考向+重难通关练+培优争分练解析版docx等2份试卷配套教学资源，其中试卷共130页， 欢迎下载使用。
一次函数、反比例函数的综合题是安徽中考命题热点。选择、填空解答题皆可出现。常见两种题型的考察方式：一是根据函数值的大小，求自变量的取值范围，一般先找交点，再分区域，根据函数图象上方的值总比下方的值大，在各区域内找相应的x的取值范围；二是求几何图形面积，要充分利用“数形结合”的思想，使“坐标”与“线段”互相转化，从而解决问题。
【考向一 函数的图象 】
一．选择题（共13小题）
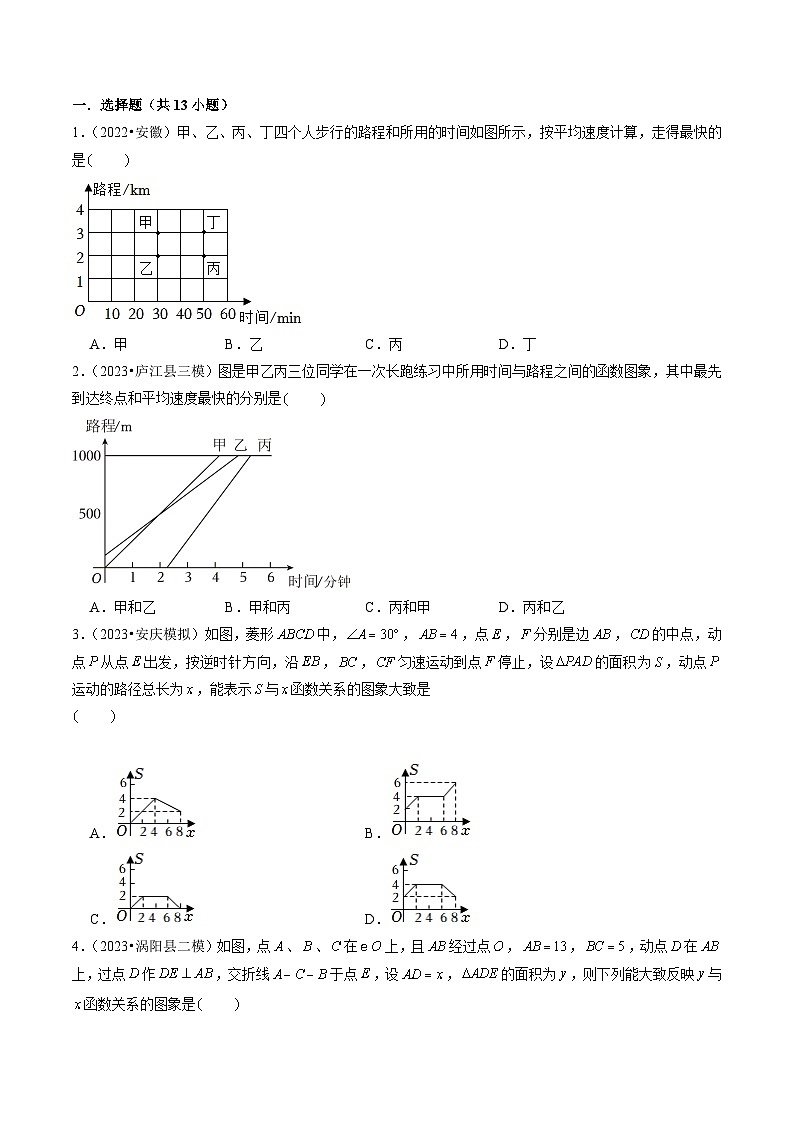
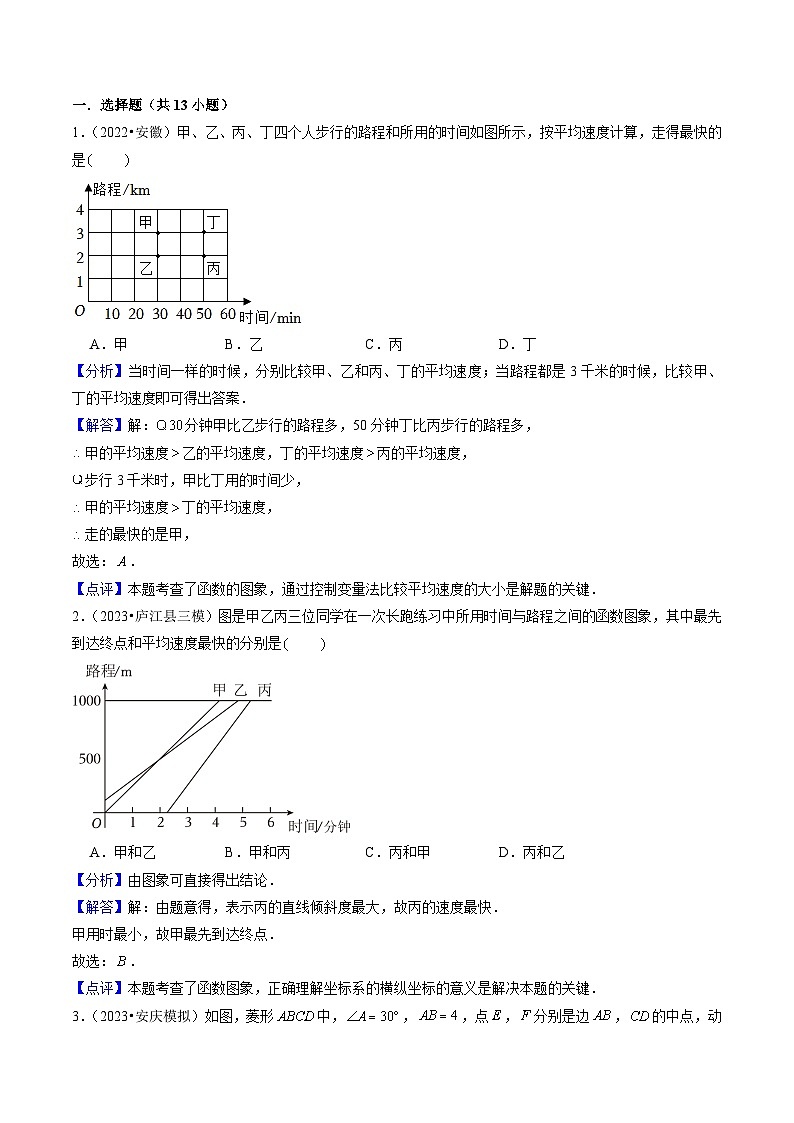
1．（2022•安徽）甲、乙、丙、丁四个人步行的路程和所用的时间如图所示，按平均速度计算，走得最快的是
A．甲B．乙C．丙D．丁
2．（2023•庐江县三模）图是甲乙丙三位同学在一次长跑练习中所用时间与路程之间的函数图象，其中最先到达终点和平均速度最快的分别是
A．甲和乙B．甲和丙C．丙和甲D．丙和乙
3．（2023•安庆模拟）如图，菱形中，，，点，分别是边，的中点，动点从点出发，按逆时针方向，沿，，匀速运动到点停止，设的面积为，动点运动的路径总长为，能表示与函数关系的图象大致是

A．B．
C．D．
4．（2023•涡阳县二模）如图，点、、在上，且经过点，，，动点在上，过点作，交折线于点，设，的面积为，则下列能大致反映与函数关系的图象是
A．B．
C．D．
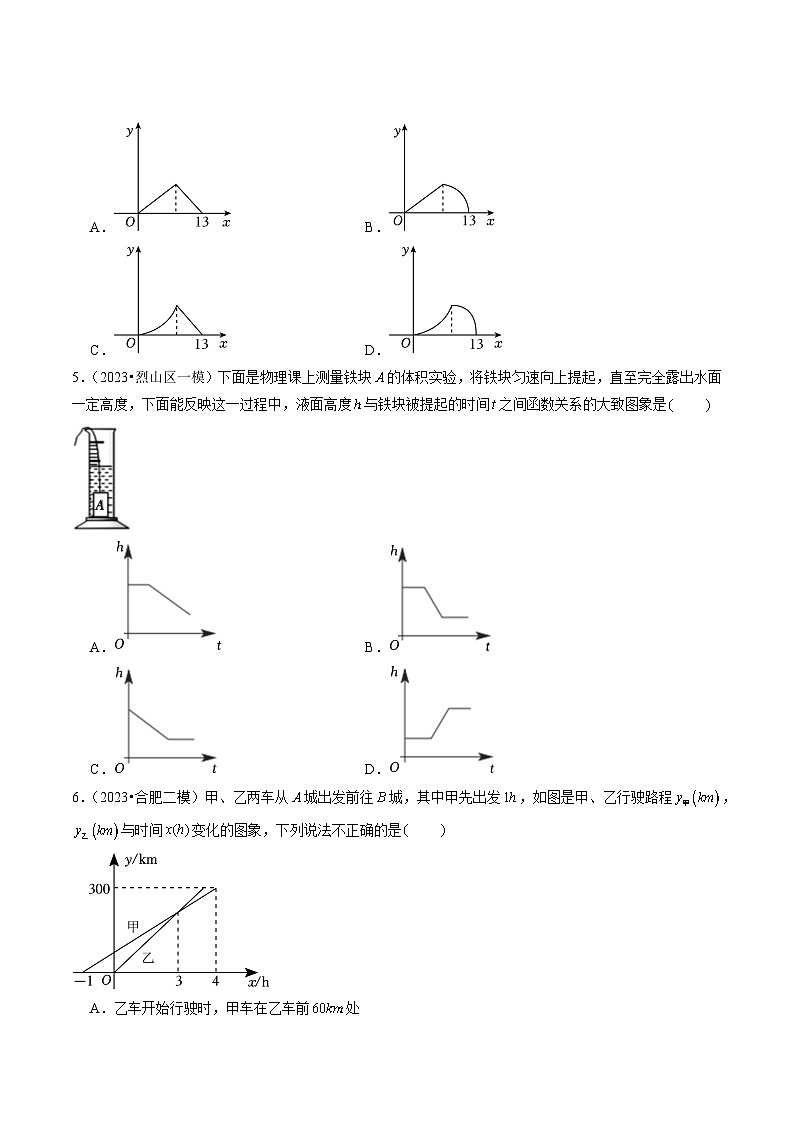
5．（2023•烈山区一模）下面是物理课上测量铁块的体积实验，将铁块匀速向上提起，直至完全露出水面一定高度，下面能反映这一过程中，液面高度与铁块被提起的时间之间函数关系的大致图象是
A．B．
C．D．
6．（2023•合肥二模）甲、乙两车从城出发前往城，其中甲先出发，如图是甲、乙行驶路程，与时间变化的图象，下列说法不正确的是
A．乙车开始行驶时，甲车在乙车前处
B．乙车的平均速度是
C．在距离城处，乙车追上甲车
D．乙车比甲车早到城
7．（2023•烈山区一模）如图（1），在中，点从点出发向点运动，在运动过程中，设表示线段的长，表示线段的长，与之间的关系如图（2）所示，则边的长是
A．B．C．D．6
8．（2023•宣城模拟）如图，在平面直角坐标系中，点，点，，点，点从点出发沿路线以每秒1个单位的速度运动，点从点出发沿路线以每秒个单位的速度运动，当一个点到达终点时另一个点随之停止运动，设，运动时间为秒，则正确表达与的关系图象是
A．B．
C．D．
9．（2023•合肥三模）如图，正方形中，，动点，分别从，同时出发，点以每秒的速度沿运动，点以每秒的速度沿运动，点到达点时运动停止．设点运动（秒时，的面积，则关于的函数图象大致为：
A．B．
C．D．
10．（2023•合肥一模）、两地相距240千米，慢车从地到地，快车从地到地，慢车的速度为120千米小时，快车的速度为180千米小时，两车同时出发．设两车的行驶时间为（小时），两车之间的路程为（千米）．则能大致表示与之间函数关系的图象是
A． B．
C． D．
11．（2020•安徽）如图，和都是边长为2的等边三角形，它们的边，在同一条直线上，点，重合．现将沿着直线向右移动，直至点与重合时停止移动．在此过程中，设点移动的距离为，两个三角形重叠部分的面积为，则随变化的函数图象大致为
A． B．
C． D．
12．（2023•安庆二模）如图，正三角形的边长为6，点从点开始沿着路线运动，过点作直线，垂足为点，连接，记点的运动路程为，的面积为，则关于的函数图象大致为
A．B．
C．D．
13．（2023•蜀山区模拟）小元步行从家去火车站，走到6分钟时，以同样的速度回家取物品，然后从家乘出租车赶往火车站，结果比预计步行时间提前了3分钟．小元离家路程（米与时间（分钟）之间的函数图象如图，那么从家到火车站路程是
A．1300米B．1400米C．1600米D．1500米
二．解答题（共1小题）
14．（2023•定远县校级模拟）如图1，在长方形中，，，点从出发，沿的路线运动，到停止；点从点出发，沿路线运动，到点停止．若、两点同时出发，速度分别为每秒、，秒时、两点同时改变速度，分别变为每秒、、两点速度改变后一直保持此速度，直到停止），如图2是的面积和运动时间（秒的图象．
（1）求出值；
（2）设点已行的路程为，点还剩的路程为，请分别求出改变速度后，、和运动时间（秒的关系式；
（3）求、两点都在边上，为何值时、两点相距？
【考向二 一次函数的图象与性质 】
一．选择题（共8小题）
1．（2023•蜀山区二模）已知函数的图象如图，则的图象可能是
A．B．
C．D．
2．（2023•霍邱县一模）一次函数的图象经过点，且的值随增大而增大，则点的坐标可能是
A．B．C．D．
3．（2023•滁州二模）一次函数的图象如图所示，则二次函数的图象经过
A．第一、二象限B．第二象限C．第三、四象限D．第三象限
4．（2023•天长市校级二模）已知，，，为直线上的三个点，且，则以下判断正确的是
A．若，则B．若，则
C．若，则D．若，则
5．（2023•东至县一模）已知二次函数的图象如图，其对称轴为，它与轴的一个交点的横坐标为，则一次函数与反比例函数在同一平面直角坐标系中的图象大致是
A．B．
C．D．
6．（2022•安徽）在同一平面直角坐标系中，一次函数与的图象可能是
A．B．
C．D．
7．（2023•金寨县校级模拟）已知一次函数，若，，则该一次函数的图象不经过
A．第一象限B．第二象限C．第三象限D．第四象限
8．（2023•庐阳区校级三模）如图，在平面直角坐标系中，直线交轴于点，交轴于点，以为边在第一象限作正方形，其中顶点恰好落在双曲线，现将正方形向下平移个单位，可以使得顶点落在双曲线上，则的值为
A．3B．C．D．2
【考向三 一次函数解析式的求法 】
一．选择题（共5小题）
1．（2023•安庆一模）一次函数的与的部分对应值如下表所示：
根据表中数据分析，下列结论正确的是
A．该函数的图象与轴的交点坐标是
B．该函数的图象经过第一、二、四象限
C．若点、均在该函数图象上，则
D．将该函数的图象向上平移5个单位长度得的图象
2．（2023•庐阳区校级三模）由于机器设备老化，某工厂去年1月份开始对部分生产设备进行技术升级，边升级边生产．去年月其利润（万元）与月份之间的变化如图所示，设备技术升级完成前是反比例函数图象的一部分，设备技术升级完成后是一次函数图象的一部分，下列说法正确的是
A．由图象可知设备技术升级完成前的五个月处于亏损状态，升级后开始盈利
B．由图象可知设备技术升级完成前后共有6个月的利润超过100万元
C．由图象可知设备技术升级完成后每月利润比前一月增加30万元
D．由图象可知设备技术升级完成后最大利润超过200万元月
3．（2023•砀山县二模）在平面直角坐标系中，将一次函数的图象向下平移4个单位长度后经过点，则的值为
A．4B．3C．2D．
4．（2023•龙子湖区二模）若将一次函数图象所在的平面直角坐标系先向上平移3个单位长度，再向右平移2个单位长度，则此时函数图象对应解析式为
A．B．C．D．
5．（2023•太和县一模）在平面直角坐标系中，若将一次函数的图象向下平移2个单位长度后经过点，则的值为
A．4B．C．0D．2
二．填空题（共1小题）
6．（2023•合肥模拟）已知某直线经过点，且与两坐标轴围成的三角形面积为2．则该直线的一次函数表达式是 ．
【考向四 一次函数与方程、不等式的关系 】
一．选择题（共6小题）
1．（2023•天长市一模）已知点在直线上，且，则下列不等关系一定成立的是
A．B．C．D．
2．（2023•怀远县校级模拟）如图，直线与直线交于点，则关于的不等式的解集为
A．B．C．D．
3．（2023•瑶海区模拟）正比例函数与一次函数的图象交于点，则关于的不等式的解集为
A．B．C．D．
4．（2023•金寨县校级模拟）已知一次函数，若，，则该一次函数的图象不经过
A．第一象限B．第二象限C．第三象限D．第四象限
5．（2023•雨山区校级一模）已知、是一次函数图象上的不同的两个点，若，则的取值范围是
A．B．C．D．
6．（2023•合肥三模）已知点在一次函数上，且，则下列不等关系一定成立的是
A．B．C．D．
二．填空题（共3小题）
7．（2023•瑶海区模拟）如图，一次函数的图象经过点，则不等式的解集为 ．
9．（2023•迎江区校级三模）如图，直线与直线相交于点，则关于的不等式的解集为 ．
三．解答题（共1小题）
10．（2023•利辛县模拟）根据学习一次函数的经验，对函数的图象进行了探究．
（1）请用“列表、描点、连线”的方法，画出这个函数的图象，并结合函数图象，写出这个函数的一条性质；
（2）已知函数的图象如图所示，结合你所画的函数图象，直接写出不等式的解集．
【考向五 一次函数的实际应用 】
一．选择题（共5小题）
1．（2021•安徽）某品牌鞋子的长度与鞋子的“码”数之间满足一次函数关系．若22码鞋子的长度为，44码鞋子的长度为，则38码鞋子的长度为
A．B．C．D．
2．（2023•庐阳区校级三模）由于机器设备老化，某工厂去年1月份开始对部分生产设备进行技术升级，边升级边生产．去年月其利润（万元）与月份之间的变化如图所示，设备技术升级完成前是反比例函数图象的一部分，设备技术升级完成后是一次函数图象的一部分，下列说法正确的是
A．由图象可知设备技术升级完成前的五个月处于亏损状态，升级后开始盈利
B．由图象可知设备技术升级完成前后共有6个月的利润超过100万元
C．由图象可知设备技术升级完成后每月利润比前一月增加30万元
D．由图象可知设备技术升级完成后最大利润超过200万元月
3．（2023•六安三模）甲，乙两人同时从相距90千米的地前往地，甲乘汽车，乙骑电动车，甲到达地停留半个小时后返回地，如图是他们离地的距离（千米）与经过时间（小时）之间的函数关系图象．当甲与乙相遇时距离地
A．16千米B．18千米C．72千米D．74千米
4．（2023•和县二模）在一条笔直的公路上、两地相距，甲车从地开往地，乙车从地开往地，甲比乙先出发．设甲、乙两车距地的路程为千米，甲车行驶的时间为小时，与之间的关系如图所示，下列说法错误的是
A．甲车的速度比乙的速度慢
B．甲车出发1小时后乙才出发
C．甲车行驶了或时，甲、乙两车相距
D．乙车达到地时，甲车离地
5．（2023•定远县校级一模）某容器有一个进水管和一个出水管，从某时刻开始的前4分钟内只进水不出水，在随后的8分钟内既进水又出水，12分钟后关闭进水管，放空容器中的水．已知进水管进水的速度与出水管出水的速度是两个常数，容器内水量（升与时间（分钟）之间的关系如图所示．则每分钟的出水量为
A．4升B．升C．升D．升
【考向六 反比例函数的图象与性质 】
一．选择题（共2小题）
1．（2023•淮南一模）如图，矩形的顶点在反比例函数的图象上，顶点，在轴上，对角线的延长线交轴于点，连接，若的面积是6，则的值为
A．B．C．D．
2．（2023•萧县一模）如图，在中，平分交于点，平分交于点，交于点，反比例函数经过点，若，，则的值为
A．B．C．D．
二．填空题（共3小题）
3．（2023•金寨县校级模拟）如图，反比例函数的图象经过点，反比例函数的图象经过点，所在直线垂直轴于点，是轴上一点，连接，，若，则的值等于 ．
4．（2023•安徽）如图，是坐标原点，的直角顶点在轴的正半轴上，，，反比例函数的图象经过斜边的中点．
（1） ；
（2）为该反比例函数图象上的一点，若，则的值为 ．
5．（2023•泗县校级模拟）如图，四边形的边与轴的正半轴重合，轴，反比例函数的图象经过四边形的对角线，的交点．若，的面积为2，则的值为 ．
【考向七 反比例函数中k的几何意义 】
一．选择题（共1小题）
1．（2023•雨山区校级一模）如图，在平面直角坐标系中，将一块直角三角形纸板如图放置，直角顶点与原点重合，顶点、恰好分别落在函数，的图象上，则的值为
A．B．C．D．
二．填空题（共10小题）
2．（2023•无为市二模）如图，点在轴的负半轴上，点在反比例函数的图象上，交轴于点，若点是的中点，的面积为，则的值为 ．
3．（2023•烈山区一模）如图，已知矩形的面积为，它的对角线与双曲线相交于点，且，则 ．
4．（2023•瑶海区校级模拟）如图，菱形的顶点在轴的正半轴上，在轴的正半轴上，点，在第一象限内，轴，反比例函数的图象经过菱形的中心，若菱形的面积为2，则的值为 ．
5．（2023•合肥三模）如图，直线与反比例函数，的图象分别交于、两点，为轴上任意一点，的面积为3，则的值为 ．
6．（2023•安徽模拟）反比例函数的图象经过，两点，为等腰三角形，轴且的面积为2，则的值为 ．
7．（2023•庐阳区校级二模）如图，点是双曲线是常数）上一点，点，是双曲线是常数）上一点，轴，轴，若四边形的面积为9，则 ．
8．（2023•蜀山区二模）如图，在平面直角坐标系中，反比例函数与一次函数的图象交于点，反比例函数图象上一点绕原点逆时针旋转至点，且，如果的面积是1，则 ．
9．（2023•裕安区校级二模）如图，菱形的顶点在轴的正半轴上，点在轴的正半轴上，点，在第一象限，且轴，点为对角线的交点，的延长线交于，反比例函数的图象经过点，若菱形的面积为16，则的值为 ．
10．（2023•安徽模拟）如图，已知函数经过点，延长交双曲线另一分支于点，过点作直线交轴正半轴于点，交轴负半轴于点，交双曲线另一分支于点，且．则的面积 ．
11．（2023•安徽模拟）如图，点在反比例函数 的图象上，点在轴上，，过点作交轴负半轴于点，连结，当面积为3时，则的值为 ．
【考向八 反比例函数与一次函数综合】
题型一：根据函数值的大小，求自变量的取值范围
1．（2023•蚌山区校级模拟）如图，在平面直角坐标系中，点的坐标为，点是直线上的一个动点，以为边，在的右侧作等边，使得点落在第一象限，连结，则的最小值为
A．6B．C．8D．
2．（2023•萧县一模）为检测某品牌一次性注射器的质量，将注射器里充满一定量的气体，当温度不变时，注射器里的气体的压强与气体体积满足反比例函数关系，其图象如图所示．
（1）求反比例函数的表达式．
（2）当气体体积为时，气体的压强为 ．
（3）若注射器内气体的压强不能超过，则其体积要控制在什么范围？
3．（2022•安徽模拟）已知一次函数，为常数，且的图象与反比例函数的图象相交于点，与轴、轴分别交于点、点．
（1）若，求的值并直接写出一次函数的值小于反比例函数的值时的取值范围；
（2）若，求的值．
4．（2022•无为市二模）已知反比例函数的图象与正比例函数的图象相交于，两点．
（1）若点的坐标为，则点的坐标为 ，当时，自变量的取值范围是 ；
（2）设点的坐标为，，点的坐标为，，求的值．（用含的代数式表示）
5．（2022•芜湖一模）已知：反比例函数的图象与一次函数的图象交于点．
（1）在同一个平面直角坐标系中，请画出函数与函数的图象；并观察图象，直接写出不等式在第一象限成立时的取值范围；
（2）已知点，，过点作垂直于轴的直线，与反比例函数图象交于点，与直线交于点．记反比例函数图象在点，之间的部分与线段，围成的区域（不含边界）为．
①当时，区域内的格点个数为 ；（格点即横、纵坐标都是整数的点）
②若区域内的格点恰好为2个，请结合函数图象，直接写出的取值范围．
题型二：求几何图形面积
1．（2022•合肥二模）如图，已知直线与双曲线的图象交于，两点，且点的坐标为．
（1）求的值和点坐标；
（2）设点，，过点作平行于轴的直线，交直线于点，交双曲线于点．若的面积大于的面积，结合图象，直接写出的取值范围．
2．（2023•萧县一模）如图，反比例函数的图象与正比例函数的图象相交于，两点．
（1）求的值及点的坐标；
（2）不等式的解集为 ；
（3）已知轴，以、为边作菱形，求菱形的面积．
3．（2023•蜀山区校级一模）如图，已知一次函数的图象与反比例函数第一象限内的图象相交于点，与轴相交于点．
（1）求和的值；
（2）如图，以为边作菱形，使点在轴正半轴上，点在第一象限，双曲线交于点，连接、，求．
（建议用时：15分钟）
一．选择题（共3小题）
1．（2023•涡阳县模拟）一个亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻控制电流的变化来实现．如图所示的是该台灯的电流（A）与电阻成反比例函数的图象，该图象经过点．根据图象可知，下列说法正确的是
A．与的函数关系式是
B．当时，
C．当时，
D．当电阻越大时，该台灯的电流（A）也越大
2．（2023•瑶海区校级模拟）已知二次函数的图象如图所示，则反比例函数与一次函数在同一平面直角坐标系的图象可能是
A．B．
C．D．
3．（2023•庐阳区校级三模）如图，是矩形的一边延长线上一点，是上一动点，连接与矩形的边交于点，连接，，若，，的面积为，设，则下列图象能反映与之间函数关系的是
A．B．
C．D．
二．填空题（共2小题）
4．（2023•南陵县校级一模）已知反比例函数的图象经过点，则 ．
5．（2023•金安区一模）如图，是反比例函数图象上的一点，过点作轴于点，使，为轴上任意一点，连接，，若，则 ．
三．解答题（共5小题）
6．（2023•岳西县校级模拟）某公司2022年投入研发费用120万元，成功研发出一种产品，产品正式投产后，生产成本为8元件．经试销发现年销售量（万件）与售价（元件）的对应关系如下表所示：
（1）直接写出关于的函数关系式；
（2）若物价部门规定每件商品的利润率不得超过，则当产品的售价为多少时，该年年利润（万元）最大？其最大年利润是多少？
7．（2023•定远县二模）如图，平面直角坐标系中，是坐标原点，直线与轴交于点，交直线于点，点从出发沿着线段以每秒1个单位的速度向点运动，运动到点停止，点从出发沿着线段以每秒1个单位的速度向点运动，当点停止时，点也停止运动，以为斜边，在的右侧作等腰直角．
（1）填空： ， ；
（2）当时求点的坐标．
8．（2023•安庆二模）已知反比例函数与一次函数交于，两点，点的纵坐标为．
（1）求一次函数解析式及与轴交点的坐标；
（2）若点与点关于原点对称，求的面积．
9．（2023•天长市校级三模）在平面直角坐标系中，一次函数，为常数，且分别交，轴于
，两点，交反比例函数的图象于第三象限的点，已知，的面积为．
（1）求的值；
（2）若，根据函数图象，写出在轴左侧一次函数值大于反比例函数值时，的取值范围．
10．（2023•蚌山区三模）如图，直线与反比例函数在第一象限内交于、两点，轴上的点满足．
（1）若点坐标为，求点的坐标；
（2）若的面积为，求实数的值；
（3）设点，的坐标分别为，，，，求的值．
（建议用时：20分钟）
一．选择题（共6小题）
1．（2023•宿州模拟）学过一次函数的知识后，某数学兴趣小组通过实验估计某液体的沸点，经过几次测量，得到如下数据：
当加热时，该液体沸腾，则其沸点温度是
A．B．C．D．
2．（2023•庐阳区模拟）函数与为常数且在同一平面直角坐标系中的大致图象是
A．B．C．D．
3．（2023•雨山区校级二模）如图，四边形为平行四边形，和平行于轴，点在函数上，点、在函数上，点在轴上，则四边形的面积为
A．13B．18C．21D．26
4．（2023•雨山区校级一模）已知是关于的方程的一个根，且点，都在反比例函数的图象上，则和满足
A．B．C．D．
5．（2023•镜湖区校级一模）如图，已知点是函数与的图象在第一象限内的交点，点在轴负半轴上，且，则的面积为
A．2B．C．4D．
6．（2023•庐阳区校级模拟）如图，在中，，，，点，同时从点出发，分别沿、运动，速度都是，直到两点都到达点即停止运动．设点，运动的时间为，的面积为，则与的函数图象大致是
A．B．
C．D．
二．填空题（共3小题）
7．（2023•庐阳区校级三模）如图，点在反比例函数的图象上，点在轴正半轴上，直线交轴于点，若，的面积为9，则的值为 ．
8．（2023•池州模拟）如图，已知点，分别在反比例函数和的图象上，以，为邻边作，点恰好落在轴上，且边交函数图象于点，当时，则 ．
9．（2023•庐阳区校级模拟）如图，直线与双曲线交于、两点，直线与双曲线在第一象限交于点，连接．则 ．
三．解答题（共7小题）
10．（2023•蚌埠模拟）在中小学生科技节中，某校展示了学生自主研制的甲、乙两种电动车搬运货物的能力．这两种电动车充满电后都可以连续搬运货物30分钟．甲种电动车先开始搬运，6分钟后，乙种电动车开始搬运．线段、分别表示两种电动车的搬运货物量（千克）与时间（分（从甲种电动车开始搬运时计时）的函数图象，根据图象提供的信息，解答下列问题：
（1）甲种电动车每分钟搬运货物量为 千克，乙种电动车每分钟搬运货物量为 千克．
（2）当时，求乙种电动车的搬运货物量（千克）与时间（分之间的函数关系式．
（3）在甲、乙两车同时搬运货物的过程中，直接写出二者搬运量相差8千克时的值．
11．（2023•天长市校级三模）2022年我省旱情严重，为支援革命老区县抗旱救灾，某工厂承担为该县生产第一批水泵的任务后日夜连续加班，生产过程中的剩余生产任务（台与已用生产时间（天之间的关系如图所示．
（1）求第一批任务需生产水泵的台数；
（2）为进一步加大支援力度，第二批生产水泵数量比第一批增加，且每台水泵售价比第一批优惠100元，这样两批水泵的总价不变，求第二批水泵每台的价格．
12．（2023•庐阳区校级三模）如图，一次函数的图象与轴、轴分别交于、两点且与反比例函数是不为0的常数）的图象在第二象限交于点，轴，垂足为，若．
（1）求的值；
（2）求两个函数图象的另一个交点的坐标；
（3）请观察图象，直接写出不等式的解集．
13．（2023•蜀山区校级一模）如图，直线与双曲线交于、两点，点的坐标为，经过点直线与轴交于点．
（1）求反比例函数的表达式以及点的坐标；
（2）点是轴上一动点，连接，若是的面积的一半，求此时点的坐标．
14．（2023•蜀山区校级三模）如图，已知反比例函数与一次函数的图象交于点、．
（1）求、、的值；
（2）求的面积；
（3）若，、，是反比例函数图象上的两点，且，，指出点、各位于哪个象限，并简要说明理由．
15．（2023•庐阳区校级一模）如图，已知一次函数与反比例函数的图象交于，两点，且与轴和轴分别交于点、点．
（1）求反比例函数与一次函数的表达式；
（2）点在轴上，且，请求出点的坐标．
16．（2023•金安区校级二模）如图，函数的图象与函数的图象相交于点．
（1）求，的值；
（2）直线与函数的图象相交于点，与函数的图象相交于点，求线段长．
满分技巧
1．函数的图象
函数的图象定义
对于一个函数，如果把自变量与函数的每一对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形就是这个函数的图象．
注意：①函数图形上的任意点（x，y）都满足其函数的解析式；②满足解析式的任意一对x、y的值，所对应的点一定在函数图象上；③判断点P（x，y）是否在函数图象上的方法是：将点P（x，y）的x、y的值代入函数的解析式，若能满足函数的解析式，这个点就在函数的图象上；如果不满足函数的解析式，这个点就不在函数的图象上．．
2．动点问题的函数图象
函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．
用图象解决问题时，要理清图象的含义即会识图．
满分技巧
1．一次函数的图象
（1）一次函数的图象的画法：经过两点（0，b）、（﹣，0）或（1，k+b）作直线y＝kx+b．
注意：①使用两点法画一次函数的图象，不一定就选择上面的两点，而要根据具体情况，所选取的点的横、纵坐标尽量取整数，以便于描点准确．②一次函数的图象是与坐标轴不平行的一条直线（正比例函数是过原点的直线），但直线不一定是一次函数的图象．如x＝a，y＝b分别是与y轴，x轴平行的直线，就不是一次函数的图象．
（2）一次函数图象之间的位置关系：直线y＝kx+b，可以看做由直线y＝kx平移|b|个单位而得到．
当b＞0时，向上平移；b＜0时，向下平移．
注意：①如果两条直线平行，则其比例系数相等；反之亦然；
②将直线平移，其规律是：上加下减，左加右减；
③两条直线相交，其交点都适合这两条直线．
2．一次函数的性质
一次函数的性质：
k＞0，y随x的增大而增大，函数从左到右上升；k＜0，y随x的增大而减小，函数从左到右下降．
由于y＝kx+b与y轴交于（0，b），当b＞0时，（0，b）在y轴的正半轴上，直线与y轴交于正半轴；当b＜0时，（0，b）在y轴的负半轴，直线与y轴交于负半轴．
3．一次函数图象上点的坐标特征
一次函数y＝kx+b，（k≠0，且k，b为常数）的图象是一条直线．它与x轴的交点坐标是（﹣，0）；与y轴的交点坐标是（0，b）．
直线上任意一点的坐标都满足函数关系式y＝kx+b．
满分技巧
待定系数法求一次函数解析式一般步骤是：
（1）先设出函数的一般形式，如求一次函数的解析式时，先设y＝kx+b；
（2）将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；
（3）解方程或方程组，求出待定系数的值，进而写出函数解析式．
注意：求正比例函数，只要一对x，y的值就可以，因为它只有一个待定系数；而求一次函数y＝kx+b，则需要两组x，y的值．
1
3
7
4
2
满分技巧
（1）一次函数与一元一次不等式的关系
从函数的角度看，就是寻求使一次函数y＝kx+b的值大于（或小于）0的自变量x的取值范围；
从函数图象的角度看，就是确定直线y＝kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
（2）用画函数图象的方法解不等式kx+b＞0（或＜0）
对应一次函数y＝kx+b，它与x轴交点为（﹣，0）．
当k＞0时，不等式kx+b＞0的解为：x＞，不等式kx+b＜0的解为：x＜；
当k＜0，不等式kx+b＞0的解为：x＜，不等式kx+b＜0的解为：x＞．
满分技巧
1、分段函数问题
分段函数是在不同区间有不同对应方式的函数，要特别注意自变量取值范围的划分，既要科学合理，又要符合实际．
2、函数的多变量问题
解决含有多变量问题时，可以分析这些变量的关系，选取其中一个变量作为自变量，然后根据问题的条件寻求可以反映实际问题的函数．
3、概括整合
（1）简单的一次函数问题：①建立函数模型的方法；②分段函数思想的应用．
（2）理清题意是采用分段函数解决问题的关键．
满分技巧
反比例函数图象上点的坐标特征
反比例函数y＝k/x（k为常数，k≠0）的图象是双曲线，
①图象上的点（x，y）的横纵坐标的积是定值k，即xy＝k；
②双曲线是关于原点对称的，两个分支上的点也是关于原点对称；
③在y＝k/x图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．
满分技巧
比例系数k的几何意义
在反比例函数y＝图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．
在反比例函数的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是|k|，且保持不变．
满分技巧
1．反比例函数与一次函数的交点问题
反比例函数与一次函数的交点问题
（1）求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．
（2）判断正比例函数y＝k1x和反比例函数y＝在同一直角坐标系中的交点个数可总结为：
①当k1与k2同号时，正比例函数y＝k1x和反比例函数y＝在同一直角坐标系中有2个交点；
②当k1与k2异号时，正比例函数y＝k1x和反比例函数y＝在同一直角坐标系中有0个交点．
2．反比例函数综合题
（1）应用类综合题
能够从实际的问题中抽象出反比例函数这一数学模型，是解决实际问题的关键一步，培养了学生的建模能力和从实际问题向数学问题转化的能力．在解决这些问题的时候我们还用到了反比例函数的图象和性质、待定系数法和其他学科中的知识．
（2）数形结合类综合题
利用图象解决问题，从图上获取有用的信息，是解题的关键所在．已知点在图象上，那么点一定满足这个函数解析式，反过来如果这点满足函数的解析式，那么这个点也一定在函数图象上．还能利用图象直接比较函数值或是自变量的大小．将数形结合在一起，是分析解决问题的一种好方法．
（元件）
11
13
15
万件
29
27
25
时间（单位：
0
10
20
30
液体温度（单位：
15
25
35
45