全国各地中考数学试卷分类汇编：开放性问题

这是一份全国各地中考数学试卷分类汇编：开放性问题，共9页。试卷主要包含了我们规定，5，b＝1，从而c＝1，先化简，再求值等内容，欢迎下载使用。


二．填空题
1．（2013•徐州，13，3分）请写出一个是中心对称图形的几何图形的名称： ．
考点：中心对称图形．
专题：开放型．
分析：常见的中心对称图形有：平行四边形、正方形、圆、菱形，写出一个即可．
解答：平行四边形是中心对称图形．故答案可为：平行四边形．
点评：本题考查了中心对称图形的知识，同学们需要记忆一些常见的中心对称图形．
2．（2013上海市，15，4分）如图3，在△和△中，点B、F、C、E在同一直线上，BF = CE，AC∥DF，请添加一个条件，使△≌△，这个添加的条件可以是____________．（只需写一个，不添加辅助线）
3.（2013四川巴中，14，3分）如图，已知点B、C、F、E在同一直线上，∠1=∠2，BC=EF，要使△ABC≌△DEF，还需添加一个条件，这个条件可以是 CA=FD ．（只需写出一个）
4．（2013江西南昌，15，3分）若一个一元二次方程的两个根分别是Rt△ABC的两条直角边长，且S△ABC=3，请写出一个符合题意的一元二次方程 ．
【答案】x2－5x+6=0
【解析】先确定两条符合条件的边长，再以它为根求作一元二次方程．
【方法指导】本题是道结论开放的题（答案不唯一），已知直角三角形的面积为3（直角边长未定），要写一个两根为直角边长的一元二次方程，我们尽量写边长为整数的情况（即保证方程的根为整数），如直角边长分别为2、3的直角三角形的面积就是3，以2、3为根的一元二次方程为；也可以以1、6为直角边长，得方程为.
5．（2013山东菏泽，12，3分）我们规定：将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“面线”. “面线”被这个平面图形截得的线段叫做该图形的“面径”（例如圆的直径就是它的“面径”) .已知等边三角形的边长为2，则它的“面径”长可以是______(写出1个即可).
【答案】或．(写出1个即可).
【解析】1）根据“三线合一”等可知，面径为底边上的高h，；（2）
与一边平行的线段（如图），设DE=x，因为△ADE与四边形
DBCE面积要相等，根据三角形相似性质，有.
解得x=. 综上所述，所以符合题意的面径只有这两种数量关系.
【方法指导】根据规定内容的定义，思考要把边长为2的等边三角形分成面积相等的两部分的直线存在有两种情形：（1）高（中线、角平分线）所在线；（2）与一边平行的线.要把一个三角形面积进行两等份，这样的直线有无数条，都过这个三角形三边中线的交点（重心）.经过计算无数条中等边三角形“面径”长只有上述两种情形.
三．解答题
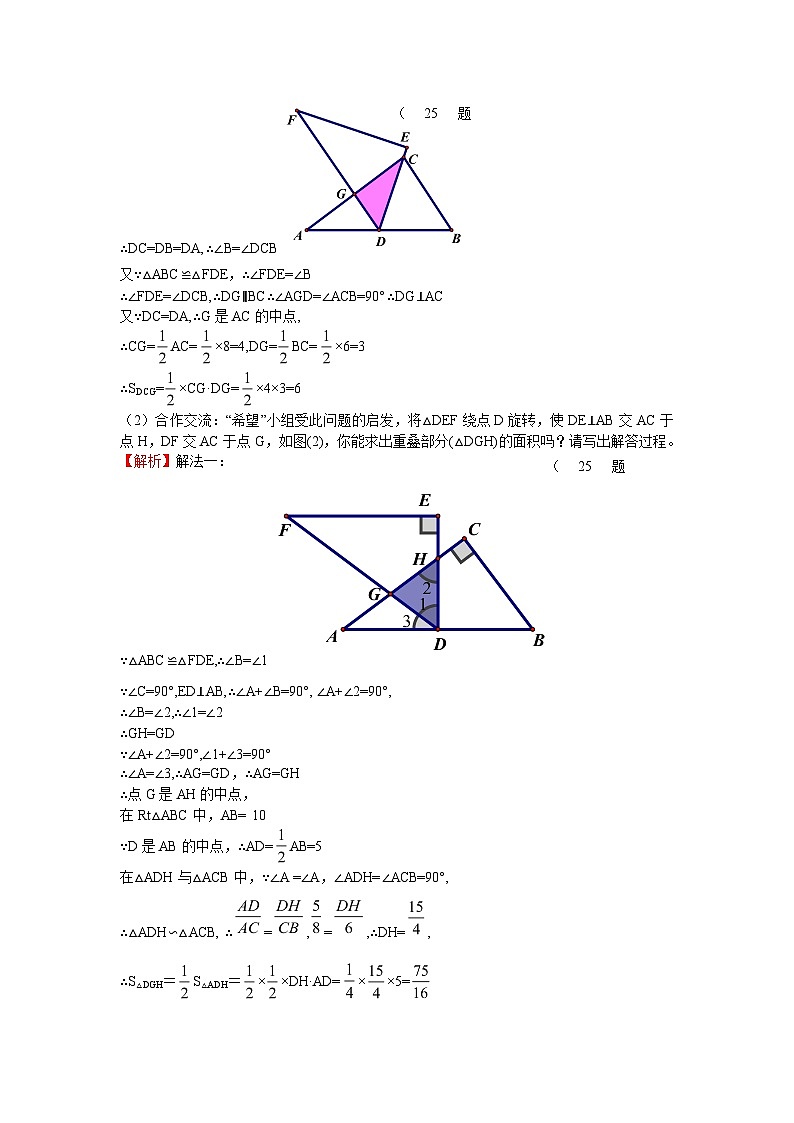
1.（2013山西，25，13分）（本题13分）数学活动——求重叠部分的面积。
问题情境：数学活动课上，老师出示了一个问题：
如图，将两块全等的直角三角形纸片△ABC和△DEF叠放在一起，其中∠ACB=∠E=90°，BC=DE=6，AC=FE=8，顶点D与边AB的中点重合，DE经过点C，DF交AC于点G。
求重叠部分（△DCG）的面积。
（1）独立思考：请解答老师提出的问题。
【解析】解：∵∠ACB=90°D是AB的中点,
（25题（1））
∴DC=DB=DA,∴∠B=∠DCB
又∵△ABC≌△FDE，∴∠FDE=∠B
∴∠FDE=∠DCB,∴DG∥BC∴∠AGD=∠ACB=90°∴DG⊥AC
又∵DC=DA,∴G是AC的中点,
∴CG=AC=×8=4,DG=BC=×6=3
∴SDCG=×CG·DG=×4×3=6
（2）合作交流：“希望”小组受此问题的启发，将△DEF绕点D旋转，使DE⊥AB交AC于点H，DF交AC于点G，如图(2)，你能求出重叠部分(△DGH)的面积吗？请写出解答过程。
（25题（2））
【解析】解法一：
∵△ABC≌△FDE,∴∠B=∠1
∵∠C=90°,ED⊥AB,∴∠A+∠B=90°, ∠A+∠2=90°,
∴∠B=∠2,∴∠1=∠2
∴GH=GD
∵∠A+∠2=90°,∠1+∠3=90°
∴∠A=∠3,∴AG=GD，∴AG=GH
∴点G是AH的中点，
在Rt△ABC中，AB= 10
∵D是AB的中点，∴AD=AB=5
在△ADH与△ACB中，∵∠A =∠A，∠ADH=∠ACB=90°,
∴△ADH∽△ACB, ∴=,=,∴DH=,
∴S△DGH＝S△ADH＝××DH·AD=××5=
（25题（2））
解法二：同解法一，G是AH的中点，
连接BH，∵DE⊥AB，D是AB的中点，∴AH=BH，设AH=x则CH＝８-ｘ
在Rt△BCH中，CH2+BC2=BH2，即（8-x）2+36=x2，解得x=
∴S△ABH=AH·BC=××6=
（25题（2））
∴S△ＤＧＨ=S△ADH=× S△ABH=×=.
解法三：同解法一，∠1=∠2
连接CD，由（1）知，∠B=∠DCB=∠1，∠1=∠2=∠B=∠DCB，△DGH∽△BDC,
作DM⊥AC于点M，CN⊥AB于点N，∵D是AB的中点，∠ACB=90°
∴CD=AD=BD，∴点M是AC的中点，∴DM=BC=×6=3
在Rt△ABC中，AB==10，AC·BC=AB·CN，
∴CN＝.
∵△DGH∽△BDC, ∴,
∴=
∴
（3）提出问题：老师要求各小组向“希望”小组学习，将△DEF绕点D旋转，再提出一个求重叠部分面积的问题。“爱心”小组提出的问题是：如图(3)，将△DEF绕点D旋转，DE，DF分别交AC于点M，N，使DM=MN求重叠部分(△DMN)的面积、
任务：①请解决“爱心”小组所提出的问题，直接写出△DMN的面积是
②请你仿照以上两个小组，大胆提出一个符合老师要求的问题，并在图中画出图形，标明字母，不必解答（注：也可在图（1）的基础上按顺时针方向旋转）。
（25题（3））
（25题（4））
【答案】①
②注：此题答案不唯一，语言表达清晰、准确得1分，画图正确得1分，重叠部分未涂阴影不扣分。示例：如图，将△DEF绕点D旋转，使DE⊥BC于点M，DF交AC于点N，求重叠部分（四边形DMCN）的面积。
2．（2013·潍坊，24，13分）如图，抛物线关于直线对称，与坐标轴交于三点，且，点在抛物线上，直线是一次函数的图象，点是坐标原点．
（1）求抛物线的解析式；
（2）若直线平分四边形的面积，求的值．
（3）把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线与直线交于两点，问在轴正半轴上是否存在一定点，使得不论取何值，直线与总是关于轴对称？若存在，求出点坐标；若不存在，请说明理由．
答案：（1）因为抛物线关于直线x＝1对称，AB＝4，所以A(－1，0)，B(3，0)，
由点D(2，1．5)在抛物线上，所以，所以3a＋3b＝1．5，即a＋b＝0．5，
又，即b＝－2a，代入上式解得a＝－0．5，b＝1，从而c＝1．5，所以．
（2）由（1）知，令x＝0，得c(0，1．5)，所以CD//AB，
令kx－2＝1．5，得l与CD的交点F()，
令kx－2＝0，得l与x轴的交点E()，
根据S四边形OEFC＝S四边形EBDF得：OE＋CF＝DF＋BE，
即
（3）由（1）知
所以把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线的解析式为
假设在y轴上存在一点P(0，t)，t＞0，使直线PM与PN关于y轴对称，过点M、N分别向y轴作垂线MM1、NN1，垂足分别为M1、N1，因为∠MPO＝∠NPO，所以Rt△MPM1∽Rt△NPN1，
所以，………………(1)
不妨设M(xM，yM)在点N(xN，yN)的左侧，因为P点在y轴正半轴上，
则（1）式变为，又yM ＝k xM－2， yN＝k xN－2，
所以（t＋2）(xM ＋xN)＝2k xM xN，……(2)
把y＝kx－2(k≠0)代入中，整理得x2＋2kx－4＝0，
所以xM ＋xN＝－2k， xM xN＝－4，代入（2）得t＝2，符合条件，
故在y轴上存在一点P（0，2），使直线PM与PN总是关于y轴对称．
考点：本题是一道与二次函数相关的压轴题，综合考查了考查了二次函数解析式的确定，函数图象交点及图形面积的求法，三角形的相似，函数图象的平移，一元二次方程的解法等知识，难度较大．
点评：本题是一道集一元二次方程、二次函数解析式的求法、相似三角形的条件与性质以及质点运动问题、分类讨论思想于一体的综合题，能够较好地考查了同学们灵活应用所学知识，解决实际问题的能力。问题设计富有梯度、由易到难层层推进，既考查了知识掌握，也考查了方法的灵活应用和数学思想的形成。
3．（2013江西南昌，18，6分）先化简，再求值：，在0，1，2，三个数中选一个合适的，代入求值．
【思路分析】先将分式的分子分母因式分解，再将除法运算转化为乘法运算，约分后得到，可通分得，也可将化为求解．
[解]原式=·+1
=
=．
当x=1时，原式=
【方法指导】本题考查的是分式的化简求值，涉及因式分解，约分等运算知识，要求考生具有比较娴熟的运算技能，化简后要从三个数中选一个数代入求值，又考查了考生的细心答题的态度，这个陷阱隐蔽但不刁钻，看到分式，必然要注意分式成立的条件．
4．（2013山东德州,22,10分）设A是由2×4个整数组成的2行4列的数表，如果某一行（或某一列）各数之和为负数，则改变该行（或该列）中所有数的符号，称为一次“操作”。
（1）数表A如表1所示，如果经过两次“操作”，使得到的数表每行的各数之和与每列的各数之和均为非负整数，请写出每次“操作”后所得的数表；（写出一种方法即可）
（2）数表A如表2所示，若经过任意一次“操作”以后，便可使得到的数表每行的各数之和与每列的各数之和均为非负整数，求整数a的值。
【思路分析】1）根据提供信息，理解题目要达到要求，答案不唯一，属于开放题（2）分析各行、各列上数字和情况，同时注意其和要符合非负数（≥0）.
【解】（1）法1：
法2：
（写出一种即可）
（2）每一列所有数之和分别为2,0,-2,0,每一行所有数之和分别为-1,1.
①如果操作第三列，则
则第一行之和为2a-1，第二行这和为5-2a，
2a-1≥0,
5-2a≥0 解得
又∵a为整数，
∴a=1 ，或a=2
②如果操作第一行，
则每一列之和分别为2-2a,2-2a2,2a-2,2a2,
2-2a≥0,
2a-2≥0 解得a=1,此时2-2a2=0, 2a2=2.
综上可知a=1
【方法指导】本题考查了新定义阅读题、分类讨论思想.本题是一道以数列为素材的新定义阅读理解题，解这类题的关键是顺着题意，理解题目的告诉了什么，要做什么？模仿或拓展运用相关知识内容解决. 本题中运用了分类讨论思想，发挥解题的多样性与严谨性.
考点：
全等三角形的判定．
专题：
开放型．
分析：
可选择添加条件后，能用SAS进行全等的判定，也可以选择AAS进行添加．
解答：
解：添加CA=FD，可利用SAS判断△ABC≌△DEF．
故答案可为CA=FD．
点评：
本题考查了全等三角形的判定，解答本题关键是掌握全等三角形的判定定理，本题答案不唯一．