最新高考数学二轮复习（新高考）【专题突破精练】 第26讲 平面向量范围与最值问题

这是一份最新高考数学二轮复习（新高考）【专题突破精练】 第26讲 平面向量范围与最值问题，文件包含第26讲平面向量范围与最值问题原卷版docx、第26讲平面向量范围与最值问题解析版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。

1、明确模拟练习的目的。不但检测知识的全面性、方法的熟练性和运算的准确性，更是训练书写规范，表述准确的过程。
2、查漏补缺，以“错”纠错。每过一段时间，就把“错题笔记”或标记错题的试卷有侧重的看一下。查漏补缺的过程也就是反思的过程，逐渐实现保强攻弱的目标。
3、严格有规律地进行限时训练。特别是强化对解答选择题、填空题的限时训练，将平时考试当作高考，严格按时完成，并在速度体验中提高正确率。
4、保证常规题型的坚持训练。做到百无一失，对学有余力的学生，可适当拓展高考中难点的训练。
5、注重题后反思总结。出现问题不可怕，可怕的是不知道问题的存在，在复习中出现的问题越多，说明你距离成功越近，及时处理问题，争取“问题不过夜”。
6、重视每次模拟考试的临考前状态的调整及考后心理的调整。以平和的心态面对高考。
第26讲 平面向量范围与最值问题
【典型例题】
例1．已知正方形的边长为1，当每个，2，3，4，5，取遍时，的最小值和最大值分别是
A．0，B．0，C．1，D．1，
【解析】解：正方形的边长为1，可得，，，
，
由于，2，3，4，5，取遍，
可得，，可取，，，，
可得所求最小值为0；
由，的最大值为4，可取，，，，，
可得所求最大值为．
故选：．
例2．已知在中，，且，则函数的最小值为
A．B．C．D．
【解析】解：中，，且，
，，
，
时，．
即函数的最小值为．
故选：．
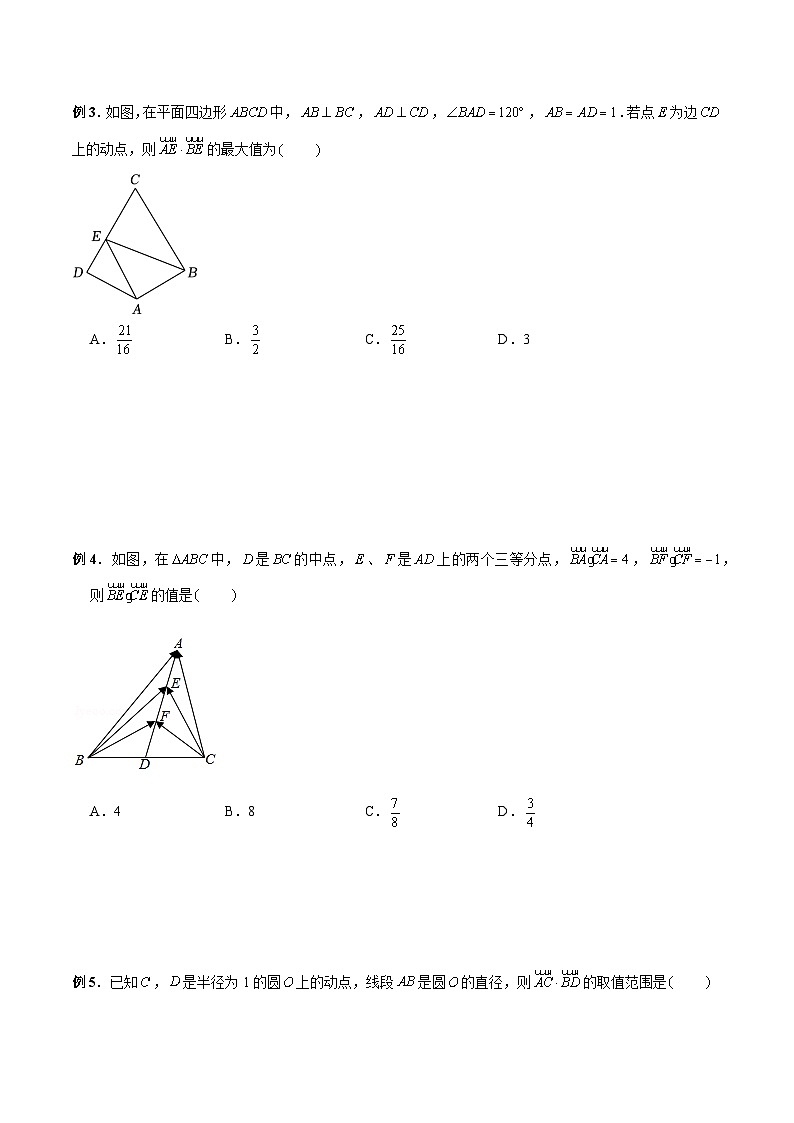
例3．如图，在平面四边形中，，，，．若点为边上的动点，则的最大值为
A．B．C．D．3
【解析】解：由题可知，和互相垂直平分，如图所示，分别以、所在的直线为和轴建立如图所示的平面直角坐标系，
则，，，，
直线的方程为，即，
设点的坐标为，
，，
开口向上，对称轴为，
当时，取得最大值，为3．
故选：．
例4．如图，在中，是的中点，、是上的两个三等分点，，，则的值是
A．4B．8C．D．
【解析】解：是的中点，，是上的两个三等分点，
，，，，
，
，
，，
又，，
，
故选：．
例5．已知，是半径为1的圆上的动点，线段是圆的直径，则的取值范围是
A．B．，C．D．，
【解析】解：如图建立平面直角坐标系：
设，，
，，，
则，，，
，，
，
其中，，，
从而，
的最大值是：，最小值是：，
最大值为：
，
当时，取最大值；
最小值是：，
当时，取最小值；
故所求范围为：，．
故选：．
例6．已知向量，满足：，向量与夹角为，则的取值范围是 ．
【解析】解：不妨设，，，
，，．
向量与夹角为，
．
，，．
在中，由正弦定理可得：，
，，
．
的取值范围是．
故答案为：．
例7．已知是边长为2的等边三角形，为内部或边界上任意一点，则的最大值为 ．
【解析】解：建立平面直角坐标系，如图所示，
中，，，，
设，则；
，，；
；
；
由图形知，当，时，取得最小值；
当，时，取得最大值2；
最大值为2，最小值为．
故答案为：2，．
【同步练习】
一．选择题
1．在平面直角坐标系中，已知点、，、是轴上的两个动点，且，则的最小值为
A．B．0C．D．
【解析】解：设点，点，，则，，
；
当时，的最小值为，
故选：．
2．设，，为平面向量，，若，则的最大值是
A．B．C．D．
【解析】解：，，，即得，，
设，，则，
因为，
整理得，
向量的终点的轨迹是以为圆心，为半径的圆．
设，，，
当直线与圆相切时，取得最大值或最小值，
此时有，解得或，
的最大值为．
故选：．
3．设为平面向量，，若，则的最大值为
A．2B．C．D．5
【解析】解：根据题意不妨设，，，
则，求的最大值，即求的最大值，
，，
，
，
关于的方程有解，△，
令，则，
，
令，则，
当时，，
，，
的最大值为：．
故选：．
4．记，，已知向量，，满足，，，，，且，则当，取最小值时，
A．B．C．1D．
【解析】解：如图，
设，则，
，，，．
又，
；
．
由，得．
，．
令．
则．
，此时，
．
．
故选：．
5．已知平面向量，，满足，，，若，，，则的取值范围是
A．B．C．D．
【解析】解：设，
由，可设，，
，
，即，
，，，
，
，解得，
，
，
．
故选：．
6．已知平面向量，，满足，，，且，则的取值范围是
A．，B．C．，D．，
【解析】解：不妨以向量，的方向分别作为，轴建立平面直角坐标系，则，，
因为，所以设，，，
所以，
所以，
设，，，
则，其中，所以，
所以，，
故，，
所以，，即，．
故选：．
7．已知为的外心，为锐角且，若，则的最大值为
A．B．C．D．
【解析】解：如图所示，以边所在直线为轴，
边的垂直平分线为轴建立直角坐标系为边的中点）．
由外接圆的性质可得．
由为锐角且，
不妨设外接圆的半径．则．
，
，．
，，，，，，
则外接圆的方程为：．
，
，，，，
，
时，否则，由图可知是不可能的．
可化为，
代入可得，
化为，
利用基本不等式可得，
化为，
解得或．
又，故应舍去．
，
则的最大值为，
故选：．
8．正三角形内一点满足，，则的值为
A．B．C．D．
【解析】解：如图，设正三角形的边长为，由得：；
；
；
得，；
；
．
故选：．
9．已知共面向量，，满足，，且．若对每一个确定的向量，记的最小值，则当变化时，的最大值为
A．B．2C．4D．6
【解析】解：如图，设，，，
，
为的中点，
，，且．若对每一个确定的向量，记的最小值，
，
，
，
设，，
在中，，
，①，
，
将①代入可得，，
，
，当且仅当时，取等号，
故选：．
10．已知向量，满足：，，，且，则的最小值为
A．B．4C．D．
【解析】解：由题意可知，把看作，
，，
则可表示为，点在直线上，
设，，
，，
，，
，
则的最小值可转化为在直线
取一点，使得最小，
作点关于的对称点，
则最小值即可求出，
设，
由，解得，，
则，
故的最小值为．
故选：．
11．已知、、、是单位圆上的相异的四个点，且、关于原点对称，则的取值范围是
A．B．C．D．
【解析】解：如图所示，因为、、、是单位圆上的相异的四个点，且、关于原点对称，
当点与点重合，点与点重合时，，
由于、、、是相异的四个点，
所以；
当点，，三点分别为，，的投影点，
则，，
所以，
当且仅当且时取等号．
综上所述，的取值范围是．
故选：．
12．边长为2的正三角形内（包括三边）有点，，则的范围是
A．，B．，C．，D．，
【解析】解：以中点为原点，所在的直线为轴，建立如图所示的坐标系，
正三角形边长为2，
，，，
设的坐标为，
，，
，
即点在的圆弧即上，
如图可以求出，；
，，，
设，则，，，
，，
又，
所以，，
当时，最大，；
当时，最小，；
所以的范围是，．
故选：．
二．填空题
13．如图，在直角梯形中，，，，，动点在以点为圆心，且与直线相切的圆上或圆内移动，设，则取值范围是 ．
【解析】解：以为坐标原点，、所在直线为轴、轴，建立平面直角坐标系如图所示．
则，，，
直线的方程为，化简得，
点到的距离，
可得以点为圆心，且与直线相切的圆方程为
．
设，则，，，
，
，，，，，
可得且，的坐标为．
在圆内或圆上，
，
设，得，
代入上式化简整理得，
若要上述不等式有实数解，
则△，
化简得，
解得，
即，
取值范围是，．
故答案为：，
14．在直角梯形中，，，，，动点在以点为圆心，且与直线相切的圆上或圆内移动，设，则最大值是 ．
【解析】解：以为坐标原点，、所在直线为轴、轴，建立平面直角坐标系如图所示．
则，，，，
则直线的方程为，
则点到直线的距离为，
可得以点为圆心，且与直线相切的圆方程为
．
设，则，，，
又，
，，，，，
可得且，的坐标为．
在圆内或圆上，
，，
设，得，
代入上式化简整理得，
若要上述不等式在，上有实数解，
对于函数，
则需，
解得，
，
又，，
故当时，取得最大值，又，
，时，取得最大值．
故答案为：．
15．已知中，，，当时，恒成立，则的面积最大值为 1 ．
【解析】解：不等式，
两边平方可得，，
由，，，可得
，
由判别式，
即为，
可得，即的最大值为，
当时，，
则的面积为；
在直角三角形中，取的中点，连接，
则，
则，
当，，三点共线时，，
又此时，
即有
．
故答案为：1，．
16．在四边形中，，，，，，则实数的值为 ．
【解析】解：，，
，，
，
；
过作，垂足为，则，，，
以为原点，以，所在直线为坐标轴建立平面坐标系如图所示：
则，设，，，
，，
，
当时，取得最小值．
故答案为：；．
17．设正的边长为1，为任意的实数，则的最小值为 ．
【解析】解：正的边长为1，为任意的实数，
，
当时，取到最小值，
的最小值为，
故答案为：．
18．已知向量，满足，，则的取值范围为 ．
【解析】解：设向量，的夹角为，，
，
令，，
，，，
即，，，，
故答案为：，．
19．已知向量，向量满足，则的取值范围是 ．
【解析】解：设，
，
，
，
化为．圆心，半径．
．
的取值范围是，，即，．
故答案为：，．
20．已知向量满足，，则的取值范围是 ．
【解析】解：由，
则，
又，，
则，
即，
则，
又，
则，
故答案为：．
21．已知向量，满足且，则的取值范围是 ．
【解析】解：，
，
，
又，
，
，
，即的取值范围是；
令，中点为，中点为，则，
又，
，
又，
当与共线时，，
．
第2小问另解：
．
故答案为：；．
22．已知向量满足，则的取值范围是 ．
【解析】解：令，反解可得，
由已知，令，
所以，
所以，
，，，
所以，
所以．
故答案为：．
23．已知向量，，满足，与的夹角为，若对一切实数，恒成立，则的取值范围为 ．
【解析】解：，，
恒成立，
恒成立，
即恒成立，
，
解得或（舍，
故答案为：，．
24．已知平面向量、、满足，，，，则最大值为 ．
【解析】解：设与所成夹角为，
则
，
因为，所以的夹角为，
设，则，
所以，设到的距离为，
则，所以，
因为，所以点落在以点为圆心，以4为半径的圆上，
所以到的距离最大值为，
所以的最大值为，
所以的最大值为．
故答案为：
25．已知平面向量，，满足，，，则的取值范围是 ．
【解析】解：，
，
，
，
当且仅当时取等号．
，
，
．
故答案为：，．
26．已知共面向量满足，，且，若对每一个确定的向量，记的最小值为，则当变化时，的最大值为 ．
【解析】解：设，，，以，为邻边作平行四边形，
由题意可知，，
，，，
过作，则的最小值为，
设，，则，
，
故答案为：2．
27．在边长为1的等边三角形中，为线段上的动点，且交于点，且交于点，则的值为 1 ．
【解析】解：设，
因为为边长为1的等边三角形，，
所以，
因为，
所以为边长为的等边三角形，，
所以，
所以；
，
所以当时， 有最小值为．
故答案为：．
28．如图，矩形中，，，，分别为线段，上的点，且满足，若，则的最小值为 ．
【解析】解：【解法一】由题意建立平面直角坐标系，如图所示；
设点，，且，；
，，；
又，
，，，，
即，
，，
，
即，
设，则；
则，
即，
故△，
即，
解得，或（不合题意，舍去）；
又在与的夹角之内，所以，，对应方程有正根；
又，，满足题意，
的最小值．
【解法二】由题意建立平面直角坐标系，如图所示；
设点，，且，；
，，；
又，
，，，，
即，
解得，；
最好运用三角换元来做比较好，根据方程组求出，（而不是，，令，，计算一个关于，的函数，比较容易看出他的最小值
故答案为：．
29．如图所示，在边长为的正方形中，动圆的半径为1，圆心在线段（含端点）上运动，是圆上及内部的动点，设向量，为实数），则的取值范围为 ．
【解析】解：如图所示，
，．
．
当圆心为点时，与相切且点在轴的下方时，．
此时，，，取得最小值；
当圆心为点时，经过圆心时，．
此时，，此时，取得最大值．
则的取值范围为，．
故答案为：，．