第一章 集合与常用逻辑用语 课件

这是一份第一章 集合与常用逻辑用语 课件，共21页。

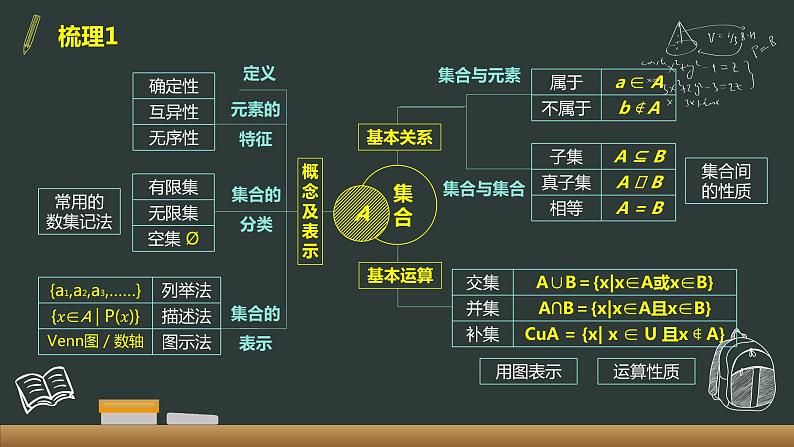
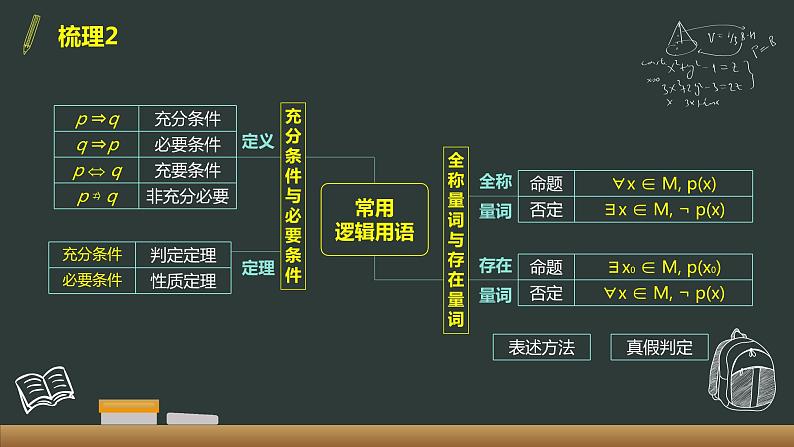
第1章 集合与常用逻辑用语章末复习【输入学校全称】1知识梳理梳理1 集 合A概念及表示定义元素的特征集合的分类集合的表示基本关系基本运算集合与元素集合与集合梳理2常用逻辑用语充分条件与必要条件全称量词与存在量词定义定理全称量词存在量词2要点精析要点①集合概念的理解及元素的特性解答集合问题，必须准确理解集合的有关概念，对于用描述法给出的集合 {?|?∈?} ，要紧紧抓住分隔符前面的代表元素x以及它所满足的条件P。例1集合?={(?,?)|? −?=0,?∈?,?∈?},?={?|?+?=1,?∈?,?∈?},则集合?∩?中元素的个数（ ） A. 0 B. 1 C. 2 D. 3 A变式集合?={(?,?)|?−?=0,?∈?,?∈?},?={（?，?)|?+?=1,?∈?,?∈?},则集合?∩?中元素的个数（ ） A. 0 B. 1 C. 2 D. 3 B要点①集合概念的理解及元素的特性关键：验证求出的a值是否满足集合中元素的“互异性”。例2设P，Q为两个非空实数集合，定义集合P+Q={a+b|a∈p,b∈Q},若P= {0，2，5} Q= {1，2，6} ，则P+Q中元素的个数是（ ） A. 8 B. 9 C. 7 D. 6A例3   要点②子集与真子集的概念（1）空集是任何集合的子集；是任何非空集合的真子集（2）任何集合都是它本身的子集例4已知集合P={1，2}，那么满足Q⊆P的集合Q的个数（ ） A. 4 B. 3 C. 2 D. 1 A变式满足Q⫋P的集合Q的个数是（ ）B引申若有限集P中有?个元素,P的子集个数为___________P的真子集个数为___________P的非空真子集个数___________   要点②子集与真子集的概念例5  要点③集合的运算例6   要点④集合的实际应用例7向50名学生调查对A、B两事件的态度，有如下结果：赞成A的人数是30，其余的不赞成，赞成B的人数是33，其余的不赞成；另外，对A、B都不赞成的学生比对A、B都赞成的学生数的三分之一多1人.问对A、B都赞成的学生和都不赞成的学生各多少人？ 归纳以上例6、例7通过数形结合方法，分别借助数轴、Venn 图，能够很直观的呈现抽象的数学语言，达到了快速清晰的解题效果。要点⑤充分条件&必要条件例8设集合M={x | x>2},N={x | x<3}，那么x ∈ M或x ∈ N是x ∈ M ∩ N的( ) A. 充要条件 B. 必要不充分条件 C. 充分不必要 D. 不充分不必要例9a∈R,|a|<3成立的一个必要不充分条件是( ) A. a<3 B. |a|<2 C. a2<9 D. 04}，B＝{x |－3≤x≤3}， 则(∁UA)∩B＝____________.【答案】　a≥3