



最新中考几何专项复习专题19 几何最值之阿氏圆巩固练习(基础)
展开策略一 建构高效的课堂教学模式-----先学后教,当堂训练。
高效的课堂教学模式是保证高效的复习效果的前提,学生在教师的指导和辅导下进行先自学、探究和及时训练,获得知识、发展能力的一种教学模式。
策略二 专题内容的设计应遵循教与学的认知规律和学生心理发展规律,凸显方法规律,由简单到复杂,由特殊到一般,再由一般到特殊
总结规律,推广一般。从一般到特殊:抛砖引玉,解决问题。
策略三 设计专题内容时考虑建立几何模型,体现思想方法,让学生驾轻就熟,化难为易,化繁为简。
几何,常常因为图形变化多端,方法多种多样而被称为数学中的变形金刚。题目千变万化,但万变不离其宗。
几何最值之阿氏圆巩固练习
1.如图,在Rt△ABC中,∠ACB=90º,CB=4,CA=6,圆C的半径为2,P为圆C上一动点,连接AP、BP,则的最小值是 .
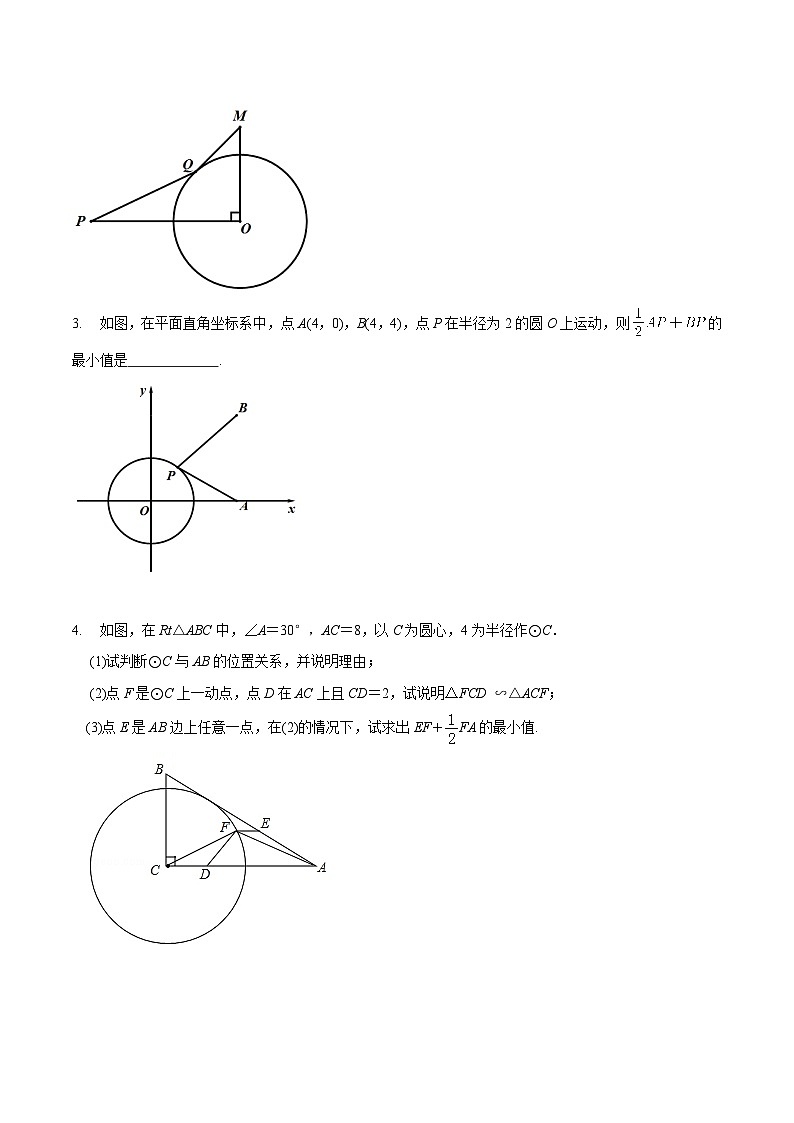
2.如图,的半径为,,MO=2,∠POM=90º,Q为上一动点,则的最小值为 .
3.如图,在平面直角坐标系中,点A(4,0),B(4,4),点P在半径为2的圆O上运动,则的最小值是 .
4.如图,在Rt△ABC中,∠A=30°,AC=8,以C为圆心,4为半径作⊙C.
(1)试判断⊙C与AB的位置关系,并说明理由;
(2)点F是⊙C上一动点,点D在AC上且CD=2,试说明△FCD ∽△ACF;
(3)点E是AB边上任意一点,在(2)的情况下,试求出EF+FA的最小值.
5.如图,抛物线y=﹣x2+bx+c与直线AB交于A(﹣4,﹣4),B(0,4)两点,直线AC:y=﹣x﹣6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=﹣x2+bx+c的表达式;
(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)在(2)的前提下,y轴上是否存在一点H,使∠AHF=∠AEF?如果存在,求出此时点H的坐标,如果不存在,请说明理由.
6.问题提出:如图1,在等边△ABC中,AB=12,⊙C半径为6,P为圆上一动点,连结AP,BP,求AP+BP的最小值.
(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图2,连接CP,在CB上取点D,使CD=3,则有==,又∵∠PCD=∠BCP,∴△PCD∽△BCP,
∴=,∴PD=BP,∴AP+BP=AP+PD.
请你完成余下的思考,并直接写出答案:AP+BP的最小值为.
(2)自主探索:如图3,矩形ABCD中,BC=7,AB=9,P为矩形内部一点,且PB=3,AP+PC的最小值为.
(3)拓展延伸:如图4,扇形COD中,O为圆心,∠COD=120°,OC=4,OA=2,OB=3,点P是上一点,求2PA+PB的最小值,画出示意图并写出求解过程.
最新中考几何专项复习专题19 几何最值之阿氏圆巩固练习(提优): 这是一份最新中考几何专项复习专题19 几何最值之阿氏圆巩固练习(提优),文件包含中考几何专项复习专题19几何最值之阿氏圆巩固练习提优教师版含解析docx、中考几何专项复习专题19几何最值之阿氏圆巩固练习提优学生版docx等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。
中考数学二轮复习专题38阿氏圆几何最值之隐形圆问题含解析答案: 这是一份中考数学二轮复习专题38阿氏圆几何最值之隐形圆问题含解析答案,共37页。试卷主要包含了如图,在中,,cm,cm等内容,欢迎下载使用。
中考数学几何专项练习:最值问题之阿氏圆: 这是一份中考数学几何专项练习:最值问题之阿氏圆,文件包含中考数学几何专项练习最值问题之阿氏圆原卷docx、中考数学几何专项练习最值问题之阿氏圆解析版docx等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。












