初中数学北师大版七年级上册第四章 基本平面图形4.3 角说课ppt课件

这是一份初中数学北师大版七年级上册第四章 基本平面图形4.3 角说课ppt课件，共39页。PPT课件主要包含了你能在图中找到角吗，公共端点，两条射线，角的顶点，角的边，角的定义，角的定义1，角的定义2，练一练，角的表示方法等内容，欢迎下载使用。

理解角的定义及有关概念.掌握角的表示方法. （重点）用运动的观点理解角、直角、平角、周角等概念.度、分、秒的转化和运算.（难点）
问题 你能找到这些角的共同特点，从而给角下一个定义吗？
1.从一点可以引出多少条射线？
2.如果从一点出发任意两条射线，出现的是什么图形？
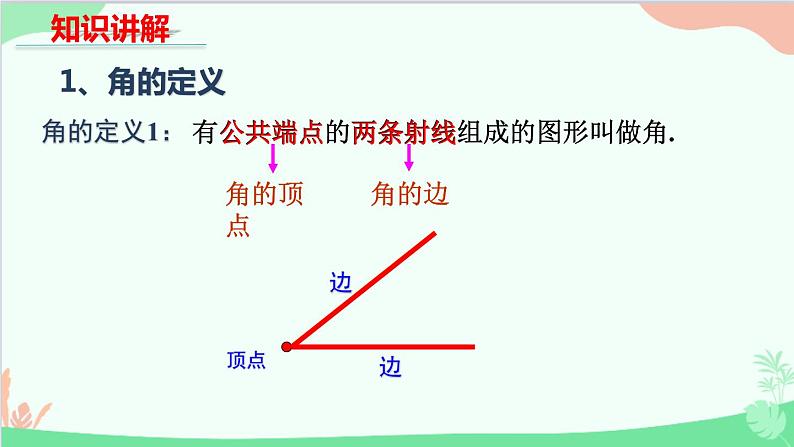
有公共端点的两条射线组成的图形叫做角.
起始位置的射线叫做这个角的始边。
终止位置的射线叫做这个角的终边。
角也可以看成是由一条射线绕它的端点旋转所组成的图形.
（2）（4）（6）是角
（1）用三个大写字母表示；
记作：∠AOB 或∠BOA
注意:顶点的字母必须写在中间
（2）用一个大写字母表示
注意:当两个或两个以上的角用同一个顶点时， 不能用一个大写字母表示．
注意：在角的内部靠近角的顶点处画一弧线，写上数字.
（4）用一个希腊字母表示
注意：在角的内部靠近角的顶点处画一弧线，写上希腊字母．
例1　如图所示，写出全部符合条件的角.
（1）能用一个大写字母表示的角；（2）能用一个数字表示的角，并将这些角用字母表示出来；（3）以点D为顶点且小于平角的角；（4）试写出图中所有小于平角的角.
解：（1）∠B.（2）∠1可用∠ABD（或∠ABC或∠ABE或∠B）表示；∠2可用∠DAC表示.（3）∠ADC（或∠ADE）和∠ADB.（4）图中小于平角的角有8个，分别是∠BAD，∠DAC（或∠2），∠BAC，∠1（或∠B或∠ABD或∠ABC或∠ABE），∠ADB，∠ADC（或∠ADE），∠ACB（或∠ACD），∠ACE.
　(a) ∠1就是∠A；
(b) ∠2就是∠B； 　　　　　　　
(c) ∠3就是∠C .
1、判断下面说法对不对：
2.如图，能把∠α记作∠O吗？∠α还可以怎么表示？
3.在上图中共有几个角？分别读出来.
三个角； ∠AOB, ∠BOC, ∠AOC.
不能 ； ∠AOB.
4.将图中的角用不同方法表示出来并填写下表.
如果一个角的终边旋转，旋转到与始边垂直时，所成的角叫做直角.
3. 直角、平角、周角
如果一个角的终边旋转，旋转到与始边成一条直线时，所成的角叫做平角.
即一个平角=180°.
当旋转到终边与始边重合时，所成的角叫做周角.
即一个周角=360°.
有人说，平角是一条直线，周角是一条射线对吗？
把一个周角360等分，每一份就是1度的角，记作1° 把1°的角60等分，每一份叫做1分的角，记作1′把1′的角60等分，每一份叫做1秒的角，记作1″
所以，角的度、分、秒是 进制的，这和时间的时、分、秒是一样的.
度 分 秒
从左往右依次进行整数保留，小数乘60
从右往左依次进行，各位除以60后再相加
例2（度、分、秒的单位换算）（1）把8.45°转化成用度、分、秒表示的形式；（2）把35°24′36″转化成用度表示的形式.
（1）0.25°等于多少分? 等于多少秒?
（1）解：60′× 0.25 = 15′ 60″× 15 = 900″ 即0.25°= 15′= 900″.
（2）2700″等于多少分? 等于多少度?
把角化成以度表示的角. 15°24′36″
解:15°24′36″=15°24′+（ ）′ =15°+（ ）° =15.41°.
问题：如何用角表示位置？ 如图所示，在平面图上的方向为“上北，下南，左西，右东”.东北方向表示以正北为角的始边，向东转45°时的射线的方向，又叫北偏东45°.东南方向为南偏东45°，西南方向为南偏西45°，西北方向为北偏西45°.方向角习惯上把南或北写在前，把东或西写在后，用两个方向表示（如北偏东60°）.
例3　如图所示是小明家和学校所在地的简单地图，已知OA＝2 km，OB＝3.5 km，OP＝4 km，点C为OP的中点，回答下列问题：（1）图中到小明家距离相同的是哪些地方？（2）由图可知，公园在小明家南偏东60°方向2 km处.请用方向与距离描述学校、商场、停车场相对于小明家的位置.
解：（1）因为点C为OP的中点，所以OC＝2 km.又因为OA＝2 km，所以可得出到小明家距离相同的是学校和公园.（2）由图可知，学校在小明家北偏东45°方向2 km处，商场在小明家北偏西30°方向3.5 km处，停车场在小明家南偏东60°方向4 km处.
1.如图所示，下列表示角的方法，不正确的是（　　）A.∠AB.∠EC.∠αD.∠12.在图中，图形的表示方法正确的有（　　） ①     ②      ③      ④A.1个B.2个 C.3个 D.4个3.2点30分时，时针与分针的夹角为（　　）A.75°B.105°C.115°D.135°
4.（1）131°28′﹣51°32′15″＝　　　　；（2）58°38′27″+47°42′40″＝　　　　.5.（1）用度、分、秒表示48.26°；（2）用度表示37°24′36″；（3）42°16′+18°23′×2；（4）90°-19°12′÷6.
5. 解：（1）48.26°＝48°+0.26×60′＝48°+15.6′＝48°15′+0.6×60″＝48°15′+36″＝48°15′36″.（2）根据1°＝60′，1′＝60″，得36″÷60＝0.6′，24.6′÷60＝0.41°，所以37°24′36″用度来表示为37.41°.（3）42°16′+18°23′×2＝42°16′+36°46′＝78°62′＝79°2′.（4）90°-19°12′÷6＝90°-18°72′÷6＝90°-3°12′＝86°48′.
6.如图所示，一幅地图上有A，B，C三地，地图被墨迹污染，C地具体位置看不清楚了，但知道C地在A地北偏东30°方向，在B地南偏东45°方向，你能确定C地的位置吗？
6.解：能，如图所示，C地在AC，BC两条射线的交点处.
某火车站的钟楼上装有一个电子报时钟，在钟面的边界上，每一分钟的刻度处都装有一只小彩灯.（1）晚上9时30分时，时针与分针所夹的角内有多少只小彩灯（包括分针处的彩灯）？（2）晚上9时35分20秒时，时针与分针所夹的角内有多少只小彩灯？  
6.解:（1）晚上9时30分时，时针与分针之间有 -30＝17.5（个）小格，中间有17个分钟刻度，而每一个分钟刻度处装有一只小彩灯，连同分针处的彩灯，时针与分针所夹的角内共有18只小彩灯.（2）晚上9时35分20秒时，时针与分针之间有＝ （个）小格，中间有12个分钟刻度，而每一个分钟刻度处装有一只小彩灯，所以晚上9时35分20秒时，时针与分针所夹的角内有12只小彩灯.
1.角的定义: 定义1:有公共端点的两条射线组成的图形叫做角，这个公共端点叫做角的顶点，这两条射线叫做角的边.
定义2： 角可以看成是由一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形.
锐角、直角、钝角、平角、周角
1、用三个大写的字母表示
2、用一个顶点的字母来表示
画上弧线，并写上希腊字母