




第15讲 几何图形的初步(28题型)(练习)-2024年中考数学一轮复习练习(全国通用)
展开2、学会运用数形结合思想。数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系,寻求代数问题的解决方法(以形助数),或利用数量关系来研究几何图形的性质,解决几何问题(以数助形)的一种数学思想。
3、要学会抢得分点。一道中考数学压轴题解不出来,不等于“一点不懂、一点不会”,要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。在研究数学问题时,我们通常是将未知问题转化为已知的问题,将复杂的问题转化为简单的问题,将抽象的问题转化为具体的问题,将实际问题转化为数学问题。
5、学会运用分类讨论的思想。如果不注意对各种情况分类讨论,就有可能造成错解或漏解,纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想:体现在数学上也就是要把难的问题转化为简单的问题,把不熟悉的问题转化为熟悉的问题,把未知的问题转化为已知的问题。
第15讲 几何图形的初步
目 录
TOC \ "1-3" \n \p " " \h \z \u
\l "_Tc155354479" 题型01 判断几何体的截面形状
\l "_Tc155354480" 题型02 判断几何体的展开图
\l "_Tc155354481" 题型03 由展开图计算几何体的表面积或体积
\l "_Tc155354482" 题型04 正方体展开图的识别
\l "_Tc155354483" 题型05 补一个面使其成为正方体的展开面
\l "_Tc155354484" 题型06 正方体相对两面上的字或图案
\l "_Tc155354485" 题型07 与七巧板有关的计算
\l "_Tc155354486" 题型08 画直线、射线、线段
\l "_Tc155354487" 题型09 直线的性质
\l "_Tc155354488" 题型10 线段的性质
\l "_Tc155354489" 题型11 与线段中点有关的计算
\l "_Tc155354490" 题型12 两点之间的距离
\l "_Tc155354491" 题型13 度、分、秒的换算
\l "_Tc155354492" 题型14 钟面角的计算
\l "_Tc155354493" 题型15 方向角的表示
\l "_Tc155354494" 题型16 角平分线的相关计算
\l "_Tc155354495" 题型17 求一个角的余角、补角
\l "_Tc155354496" 题型18 与余角、补角有关的计算
\l "_Tc155354497" 题型19 同(等)角的余(补)角相等
\l "_Tc155354498" 题型19 点到直线的距离
\l "_Tc155354499" 题型20 利用对顶角、邻补角的性质求解
\l "_Tc155354500" 题型21 判断同位角、内错角、同旁内角
\l "_Tc155354501" 题型22 利用平行线的判定进行证明
\l "_Tc155354502" 题型23 平行线判定的实际应用
\l "_Tc155354503" 题型24 由平行线的性质求角度
\l "_Tc155354504" 题型25 由平行线的性质解决折叠问题
\l "_Tc155354505" 题型26 平行线的性质在实际生活的应用
\l "_Tc155354506" 题型26 利用平行线的性质解决三角板问题
\l "_Tc155354507" 题型27 根据平行线性质与判定求角度
\l "_Tc155354508" 题型28 根据平行线性质与判定证明
题型01 判断几何体的截面形状
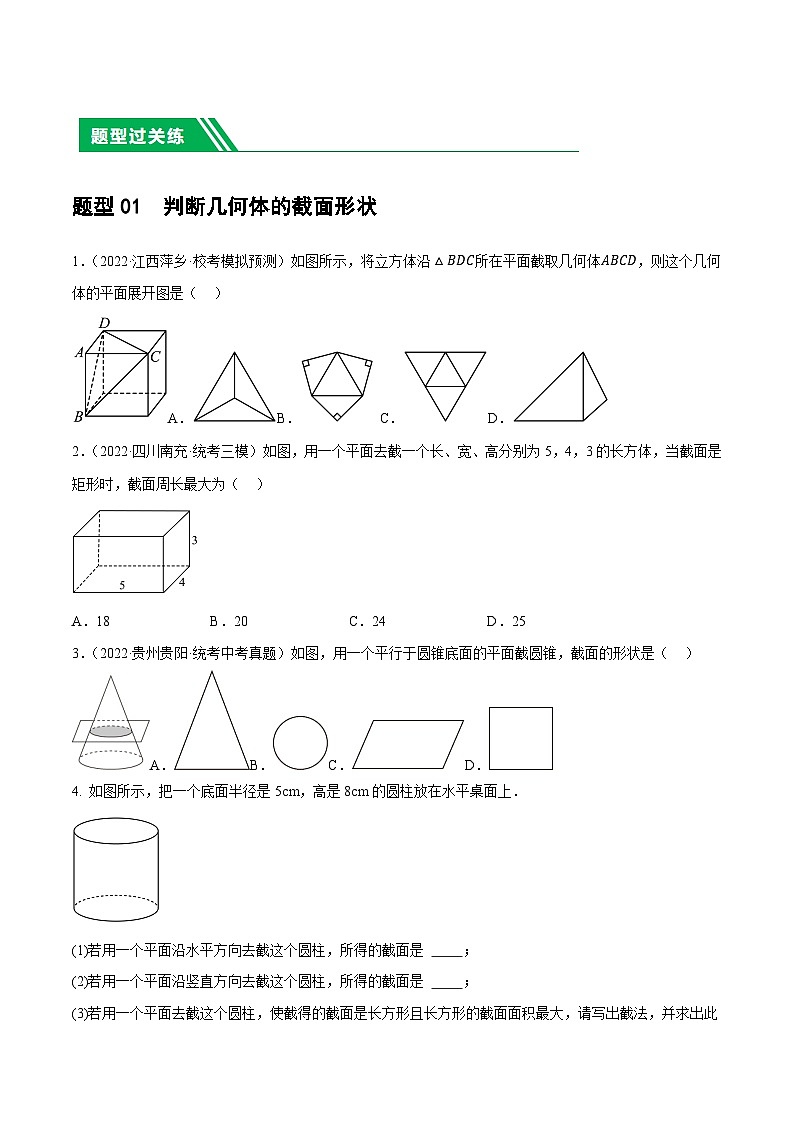
1.(2022·江西萍乡·校考模拟预测)如图所示,将立方体沿△BDC所在平面截取几何体ABCD,则这个几何体的平面展开图是( )
A.B.C.D.
2.(2022·四川南充·统考三模)如图,用一个平面去截一个长、宽、高分别为5,4,3的长方体,当截面是矩形时,截面周长最大为( )
A.18B.20C.24D.25
3.(2022·贵州贵阳·统考中考真题)如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A.B.C.D.
4. 如图所示,把一个底面半径是5cm,高是8cm的圆柱放在水平桌面上.
(1)若用一个平面沿水平方向去截这个圆柱,所得的截面是 ;
(2)若用一个平面沿竖直方向去截这个圆柱,所得的截面是 ;
(3)若用一个平面去截这个圆柱,使截得的截面是长方形且长方形的截面面积最大,请写出截法,并求出此时截面面积.
题型02 判断几何体的展开图
1.(2021·北京·统考中考真题)如图是某几何体的展开图,该几何体是( )
A.长方体B.圆柱C.圆锥D.三棱柱
2.(2021·浙江·统考中考真题)将如图所示的长方体牛奶包装盒沿某些棱剪开,且使六个面连在一起,然后铺平,则得到的图形可能是( )
A.B.C.D.
3.(2021·江苏扬州·统考中考真题)把图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )
A.五棱锥B.五棱柱C.六棱锥D.六棱柱
4.(2021·浙江绍兴·统考一模)如图,已知圆柱底面的直径BC=8,圆柱的高AB=10,在圆柱的侧面上,过点A,C嵌有一圈长度最短的金属丝.
(1)现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是______.
A.;B.;C.;D.
(2)求该长度最短的金属丝的长.
题型03 由展开图计算几何体的表面积或体积
1.(2023·浙江杭州·统考一模)如图为一个长方体的展开图,且长方体的底面为正方形.根据图中标示的长度,求此长方体的体积为 .
2.(2022·山东青岛·青岛大学附属中学校考一模)如图,以边长为63cm的正六边形纸板的各顶点为端点,在各边上分别截取4cm长的12条线段,过截得的12端点作所在边的垂线,形成6个有两个直角的四边形.把它们沿图中虚线减掉,用剩下的纸板折成一个底为正六边的无盖柱形盒子,则它的容积为 cm3.
3.(2021·辽宁抚顺·统考一模)某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1.
(1)由三视图可知,密封纸盒的形状是__________;
(2)根据该几何体的三视图,在图2中补全它的表面展开图;
(3)请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)
4.(2020·河北邯郸·校考一模)如图(1)是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)图(2)是根据a,h的取值画出的几何体的主视图和俯视图,请在网格中画出该几何体的左视图;
(2)已知h=4,求a的值和该几何体的表面积.
题型04 正方体展开图的识别
1.(2021·广东·统考中考真题)下列图形是正方体展开图的个数为( )
A.1个B.2个C.3个D.4个
2.(2022·黑龙江绥化·统考中考真题)下列图形中,正方体展开图错误的是( )
A.B.C.D.
3.(2021·浙江金华·统考一模)下列哪个图形不可能是正方体的表面展开图( )
A.B.C.D.
题型05 补一个面使其成为正方体的展开面
1.(2022·河北承德·统考二模)如图,方格纸上每个小正方形的边长都相同,若使阴影部分能折叠成一个正方体,则需剪掉的一个小正方形不可以是( )
A.①B.②C.③D.④
2.(2021·河南洛阳·统考二模)如图,在有序号的方格中选出一个画出阴影,使它与图中五个有阴影的正方形一起可以构成正方体表面的展开图,正确的选法是( )
A.只有②B.只有①④C.只有①②④D.①②③④都正确
3.(2021·浙江杭州·一模)已知图1的小正方形和图2中所有的小正方形都全等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形是不能围成一个正方体的.那么安放的位置是( )
A.①B.②C.③D.④
题型06 正方体相对两面上的字或图案
1.(2021·河北唐山·统考三模)如图是一个正方体的平面展开图,正方体中相对的面上的数字或代数式互为相反数.则
(1)x的值为 ;
(2)x2−y的值为 .
2.(2022·陕西宝鸡·统考模拟预测)如图是正方体的一种展开图,则原正方体中与“真”所在面的对面所标的字是 .
3.(2021·河北唐山·统考一模)如图是一个正方体纸盒的表面展开图,纸盒中相对两个面上的数互为相反数.
(1)填空:a=______,b=_______,c=_______;
(2)将2a(a−b)+b(2a−b−c)化简,并代入求值.
4.(2021·河北邢台·统考一模)把如图所示的正方形展开,得到的平面展开图可以是( )
A.B.C.D.
5.(2022·河南洛阳·统考三模)如图是一个正方体,下列哪个选项是它的展开图( )
A.B.C.D.
6.(2021·吉林长春·东北师大附中校考二模)将一个小正方体按图中所示的方式展开,则在展开图中表示棱a的线段可以是( )
A.线段CDB.线段EFC.线段ADD.线段BC
题型07 与七巧板有关的计算
1.(2020·浙江湖州·统考中考真题)七巧板是我国祖先的一项卓越创造,流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板,如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形,则这两个图形中,中国七巧板和日本七巧板能拼成的个数分别是( )
A.1和1B.1和2C.2和1D.2和2
2.(2022·江西赣州·统考三模)七巧板是由可以错综分合的几何图案演化而来,它是一种拼板玩具,体现了我国古代劳动人民的智慧,如图1,将一块正方形薄板分为7块,其中包括5块大小不等的三角形,1块正方形和1块平行四边形,图2是由图1拼成的风车形状,则下列等式错误的是( )
A.S5+S7=S2B.2S6=S3C.S7=13S1D.S7=S3
3.(2021·浙江金华·统考三模)七巧板是我国祖先的一项卓越创造,下列四幅图是爱思考的小红同学用如图所示的七巧板拼成的,则这四个图形的周长从大到小排列正确的是( )
A.乙>丙>甲>丁B.乙>甲>丙>丁
C.丙>乙>甲>丁D.丙>乙>丁>甲
4.(2022·湖南株洲·统考二模)七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,也被誉为“东方魔板”.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”).图①是由边长为8cm的正方形薄板分为7块制作成的“七巧板”,图②是用该“七巧板”拼成的一个“家”的图形.该“七巧板”中7块图形之一的正方形(阴影部分)面积为 cm2.
5.(2022·陕西西安·校考二模)如图(1)是边长为8cm的正方形纸片做成的七巧板,用这副七巧板拼成图(2)所示的房屋形状,则该房屋形状的面积是 cm2.
6.(2020·湖北黄石·校考模拟预测)动手做一做:某校教具制作车间有等腰三角形正方形、平行四边形的塑料若干,数学兴趣小组的同学利用其中7块恰好拼成一个矩形(如图1),后来又用它们拼出了XYZ等字母模型(如图2、图3、图4),每个塑料板保持图1的标号不变,请你参与:
(1)将图2中每块塑料板对应的标号填上去;
(2)图3中,只画出了标号7的塑料板位置,请你适当画线,找出其他6块塑料板, 并填上标号;
(3)在图4中,找出7块塑料板,并填上标号.
题型08 画直线、射线、线段
1.(2022·河北秦皇岛·统考一模)如图,∠AOB的一边OB经过的点是( )
A.P点B.Q点C.M点D.N点
2.(2022·河北邢台·校考三模)如图,已知A,B,C三点,画直线AB,画射线AC,连接BC,按照上述语句画图,下列正确的是( )
A. B. C. D.
3.(2020·浙江杭州·模拟预测)如图,已知平面上四个点A,B,C,D,按下列要求画出图形:
(1)画线段BD和线段BD的延长线;
(2)线段AC和线段DB相交于点O;
(3)连结线段BC,反向延长线段BC.
题型09 直线的性质
1.(2022·广东深圳·模拟预测)数学知识在生产和生活中被广泛应用,下列实例所应用的最主要的几何知识,说法正确的是( )
A.学校门口的伸缩门由菱形而不是其他四边形组成,应用了“菱形的对角线互相垂直平分”
B.车轮做成圆形,应用了“圆是中心对称图形”
C.射击时,瞄准具的缺口、准星和射击目标在同一直线上,应用了“两点确定一条直线”
D.地板砖可以做成矩形,应用了“矩形对边相等”
2.(2023·陕西西安·模拟预测)如图,锯木板前,在木板两端固定两个点,用墨盒弹一根墨线然后再锯,这样做的数学道理是( )
A.两点之间线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
题型10 线段的性质
1.(2022·江苏扬州·统考一模)下列三个日常现象:
其中,可以用“两点之间线段最短”来解释的是( )
A.①B.②C.③D.②③
2.(2021·浙江台州·统考中考真题)小光准备从A地去往B地,打开导航、显示两地距离为37.7km,但导航提供的三条可选路线长却分别为45km,50km,51km(如图).能解释这一现象的数学知识是( )
A.两点之间,线段最短B.垂线段最短
C.三角形两边之和大于第三边D.两点确定一条直线
3.(2023·北京海淀·统考一模)在一条沿直线MN铺设的电缆两侧有甲、乙两个小区,现要求在MN上选取一点P,向两个小区铺设电缆.下面四种铺设方案中,使用电缆材料最少的是( )
A.B.C.D.
题型11 与线段中点有关的计算
1.(2023·浙江·模拟预测)如图,A,B两地相距1200m,小车从A地出发,以8m/s的速度向B地行驶,中途在C地停靠3分钟.大货车从B地出发,以5m/s的速度向A地行驶,途经D地(在A地与C地之间)时沿原路返回B点取货两次,且往返两次速度都保持不变(取货时间不计),取完两批货后再出发至A点.已知:AC=3BC,CD=100m,则直至两车都各自到达终点时,两车相遇的次数为( )
A.2B.3C.4D.5
2.(2023·河北秦皇岛·统考一模)如图,数轴上的三个点A,B,C分别表示实数a,b,c.
(1)如果点C是AB的中点,那么a,b,c之间的数量关系是__________,
(2)比较b−2与c+1的大小,并说明理由;
(3)化简:−|a−2|+|b+1|+|c|.
3.(2023·山西太原·山西大附中校考模拟预测)已知线段a、b、c.
(1)用直尺和圆规作出一条线段AB,使它等于a+c−b.(保留作图痕迹,检查无误后用水笔描黑,包括痕迹)
(2)若a=6,b=4,c=7,点C是线段AB的中点,求AC的长.
4.(2023·河北衡水·校联考模拟预测)如图,已知数轴上点A,B对应的数为−5,1,点C为AB的中点,点P为数轴上任意一点,且对应的数为m.
(1)若点P为原点,在图中标出点P的位置,并直接写出点C对应的数;
(2)若点P在B的右侧且满足AP=3PB,求−5,1与m这三个数的和.
题型12 两点之间的距离
1.(2020·河北唐山·统考一模)A、B、C、D四个车站的位置如图所示.
(1)A、D两站的距离为_________;
(2)C、D两站的距离为__________;
(3)若a=3,C为AD的中点,求b的值.
2.(2020·浙江杭州·模拟预测)如图所示,M是线段AB上一定点,AB=12cm,C,D两点分别从点M,B出发以1cm/s,2cm/s的速度沿直线BA向左运动,运动方向如箭头所示(点C在线段AM上,点D在线段BM上).
(1)当点C,D运动了2s时,求AC+MD的值.
(2)若点C,D运时,总有MD=2AC,则AM=_______.
(3)在(2)的条件下,N是直线AB上一点,且AN−BN=MN,求MNAB的值.
3.(2020·河北·统考模拟预测)如图,在数轴上有A,B两点,点A在点B的左侧.已知点B对应的数为2,点A对应的数为a.
(1)若a=﹣1,则线段AB的长为 ;
(2)若点C到原点的距离为3,且在点A的左侧,BC﹣AC=4,求a的值.
4.(2021·河北邯郸·一模)如图,在一条不完整的数轴上,从左到右的点A,B,C把数轴分成①②③④四部分,点A,B,C对应的数分别是a,b,c,已知bc<0.
(1)请直接写出原点在第几部分;
(2)若AC=5,BC=3,b=﹣1,求a;
(3)若点C表示数3,数轴上一点D表示的数为d,当点C、原点、点D这三点中其中一点是另外两点的中点时,直接写出d的值.
题型13 度、分、秒的换算
1.(2021·内蒙古呼伦贝尔·统考中考真题)74°19'30″= °.
2(2023·江苏盐城·校考一模)已知∠A=65°30',则∠A的补角= °.
3.(2020·浙江湖州·统考模拟预测)计算:40°﹣15°30′= .
题型14 钟面角的计算
1.(2019·广西梧州·统考中考真题)如图,钟表上10点整时,时针与分针所成的角是( )
A.30°B.60°C.90°D.120°
2.(2022·安徽安庆·统考二模)如图表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点 30分时,分针垂直于桌面,A点距桌面的高度为10厘米,如图①. 若此钟面显示3点45分 时,A点距桌面的高度为18厘米,如图②. 则钟面显示3点50分时,A点距桌面的高度为( )厘米
A.22−33B.16+πC.22D.18+43
3.(2018·山东德州·校联考一模)在下列时间段内时钟的时针和分针会出现重合的是( )
A.5:20-5:26B.5:26-5:27C.5:27-5:28D.5:28-5:29
题型15 方向角的表示
1.(2022·河北石家庄·统考一模)如图,嘉琪从点A出发,沿正东方向前进5m后向左转30°,再前进5m后又向左转30°,这样一直走下去.以下说法错误的是( )
A.第二次左转后行走的方向是北偏东30°B.第六次左转后行走的方向是正西方向
C.第八次左转后行走的方向是南偏西60°D.嘉琪第一次回到点A时,一共走了60m
2.(2022·河北石家庄·校考一模)A,B,C三地两两的距离如图所示,B地在A地的正西方向,下面说法不正确的是( )
A.C地在B地的正北方向上B.A地在B地的正东方向上C.C地在A地的北偏西60°方向上D.A地在C地的南偏东30°方向上
3.(2023·河北秦皇岛·统考二模)如图,有A,B,C三地,B地在A地北偏西36°方向上,AB⊥BC,则B地在C地的( )
A.北偏西54°方向B.北偏东54°方向C.南偏西54°方向D.南偏西90°方向
题型16 角平分线的相关计算
1.(2021·山东济南·统考中考真题)如图,AB//CD,∠A=30°,DA平分∠CDE,则∠DEB的度数为( )
A.45°B.60°C.75°D.80°
2.(2020·四川乐山·中考真题)如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF.则∠GEB=( )
A.10°B.20°C.30°D.40°
3.(2018·四川南充·统考一模)如图,已知OC是∠AOB内部任意的一条射线,OM、ON分别是∠AOC、∠BOC的平分线.
(1)若∠AOM=20°,∠BON=30°,求∠MON的度数;
(2)若∠AOB=α,求∠MON的度数.
4.(2020·浙江杭州·模拟预测)已知O是直线AB上一点,将一个直角三角尺OMN按图①方式放置,直角边ON在直线AB上,另一条直角边OM与AB的夹角∠AOM=90°,射线OC在∠AOM内部.
(1)如图②,将三角尺OMN绕着点O顺时针旋转,当OM平分∠BOC时,试判断∠AON与∠CON的大小关系,并说明理由.
(2)若∠AOC=60°,三角尺OMN绕点O顺时针旋转一周,每秒旋转5°,旋转时间为t,则当t为何值时∠CON=∠MOB?
(3)在(2)的条件下,在三角尺OMN绕点O顺时针旋转一周的过程中,∠CON+∠MOB的值能否为定值?若能,求t的取值范围.
题型17 求一个角的余角、补角
1.(2021·广西百色·统考中考真题)已知∠α=25°30′,则它的余角为( )
A.25°30′B.64°30′C.74°30′D.154°30′
2.(2019·甘肃兰州·一模)一个角的补角是150°,则这个角的余角等于( )
A.30°B.40°C.50°D.60°
3.(2022·广东东莞·东莞市东城实验中学校联考一模)若一个角的余角是25°,那么这个角的度数是 .
4.(2022·江苏苏州·苏州中学校考二模)(1)已知∠α=35°19′,则∠α的余角等于 ;
(2)已知∠β的补角为120°37′46″,∠β= °.
题型18 与余角、补角有关的计算
1.(2021·陕西西安·校考模拟预测)如图,∠AOC与∠COB互余,∠COB=15°,OC平分∠AOD,则∠BOD的度数是( )
A.75°B.60°C.65°D.55°
2.(2023·广东河源·三模)任意一个锐角的补角与这个锐角的余角的差等于 °.
3.(2022·云南昆明·云大附中校考模拟预测)若∠1与∠2互补,∠3与∠1互余,∠2+∠3=120°,则∠2−∠1= .
题型19 同(等)角的余(补)角相等
1.(2020·北京房山·统考一模)一副直角三角板有不同的摆放方式,图中满足∠α与∠β相等的摆放方式是( )
A.B.C.D.
2.(2023·福建厦门·厦门一中校考一模)如图,在直角△ABC中,∠ACB=90°,CD⊥AB于点D,则sinA=( )
A.BCACB.ACABC.ADACD.BDBC
3.将一副三角板按如图方式摆放,∠1与∠2不一定互补的是( )
A.B.C.D.
4.(2020·黑龙江大庆·统考中考真题)将两个三角尺的直角顶点重合为如图所示的位置,若∠AOD=108°,则∠COB= .
题型19 点到直线的距离
1.(2022·山东淄博·模拟预测)如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若AD=13,AC=12,则点D到AB的距离为( )
A.3B.4C.5D.6
2.(2023下·广东深圳·九年级校联考阶段练习)如图,∠ABC=∠ADB=90°,DA=DB,若BC=2,AB=4,则点D到AC的距离是( )
A.556B.655C.455D.554
3.(2021·山东滨州·二模)阅读下面材料:
我们知道一次函数y=kx+b(k≠0,k、b是常数)的图象是一条直线,到高中学习时,直线通常写成Ax+By+C=0(A≠0,A、B、C是常数)的形式,点P(x0,y0)到直线Ax+By+C=0的距离可用公式d=|Ax0+By0+C|A2+B2计算.
例如:求点P(3,4)到直线y=﹣2x+5的距离.
解:∵y=﹣2x+5
∴2x+y﹣5=0,其中A=2,B=1,C=﹣5
∴点P(3,4)到直线y=﹣2x+5的距离为: d=|Ax0+By0+C|A2+B2=|2×3+1×4−5|22+12=55=5
根据以上材料解答下列问题:
(1)求点Q(﹣2,2)到直线3x﹣y+7=0的距离;
(2)如图,直线l1:y=﹣x沿y轴向上平移2个单位得到另一条直线l2,求这两条平行直线之间的距离.
(3)若将l2绕其与y轴的交点逆时针旋转90度与l1相交,直接写出l1大于l2时,x的取值范围
题型20 利用对顶角、邻补角的性质求解
1.(2022·北京·统考中考真题)如图,利用工具测量角,则∠1的大小为( )
A.30°B.60°C.120°D.150°
2.(2020·贵州安顺·统考中考真题)如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是( )
A.150°B.120°C.60°D.30°
3.(2021·河南·统考中考真题)如图,a//b,∠1=60°,则∠2的度数为( )
A.90°B.100°C.110°D.120°
4.(2020·湖北黄冈·中考真题)已知:如图,AB//EF,∠ABC=75°,∠CDF=135°,则∠BCD= 度.
题型21 判断同位角、内错角、同旁内角
1.(2021·广西百色·统考中考真题)如图,与∠1是内错角的是( )
A.∠2B.∠3C.∠4D.∠5
2.(2018·浙江金华·中考真题)如图,∠B的同位角可以是( )
A.∠1B.∠2C.∠3D.∠4
题型22 利用平行线的判定进行证明
1.(2022·湖北武汉·校考三模)如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
(1)求证:EF∥AD;
(2)求证:∠BAC+∠AGD=180°.
2.(2022·湖北武汉·校考模拟预测)如图,AB∥CD,AM平分∠BAE,FG平分∠AFC.
(1)求证:AM∥GF;
(2)若∠BAM=55°,求∠CFE的度数.
3.(2022·安徽合肥·合肥38中校考一模)如图,在△ABC中,AB=AC,点E在边BC的延长线上,以AC为边作△ACD,使DA=DC,且点B、D在AC的两侧,连接AE交CD于点F,若∠ADC=∠BAC.
(1)求证:AD∥BE;
(2)求证:AC2=BC⋅CD;
(3)若DA=10、CE=2.5,且AC2=2CF⋅AD,求AE的长;
题型23 平行线判定的实际应用
1.(2020·浙江金华·统考中考真题)如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a//b,理由是( )
A.在同一平面内,垂直于同一条直线的两条直线平行
B.在同一平面内,过一点有且仅有一条直线垂直于已知直线
C.连接直线外一点与直线各点的所有直线中,垂线段最短
D.经过直线外一点,有且只有一条直线与这条直线平行
2.(2019·辽宁抚顺·九年级统考阶段练习)如图,将木条a,b与c钉在一起,∠1=85°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )
A.15°B.25°C.35°D.50°
3.(2021·山东烟台·统考中考真题)《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=1米,AC=1.6米,AE=0.4米,那么CD为 米.
题型24 由平行线的性质求角度
1.(2022·辽宁鞍山·统考中考真题)如图,直线a∥b,等边三角形ABC的顶点C在直线b上,∠2=40°,则∠1的度数为( )
A.80°B.70°C.60°D.50°
2.(2022·辽宁·统考中考真题)如图,直线m∥n,AC⊥BC于点C,∠1=30°,则∠2的度数为( )
A.140°B.130°C.120°D.110°
3.(2022·甘肃平凉·模拟预测)如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点B'处,若∠1=∠2=36°,∠B为( )
A.36°B.144°C.108°D.126°
4.(2021·山东临沂·统考中考真题)如图,在AB//CD中,∠AEC=40°,CB平分∠DCE,则∠ABC的度数为( )
A.10°B.20°C.30°D.40°
题型25 由平行线的性质解决折叠问题
1.(2022·四川达州·模拟预测)如图,生活中,将一个宽度相等的纸条按图所示折叠一下,如果∠1=140°,那么∠2的度数为( )
A.140°B.120°C.110°D.100°
2.(2023·湖南娄底·统考模拟预测)如图,把△ABC沿平行于BC的直线DE折叠,使点A落在边BC上的点F处,若∠B=50°,则∠BDF的度数为 .
3.(2023·广东湛江·统考二模)如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF.若∠ABE=20°,则∠EFC'的度数为 .
4.(2023·河北秦皇岛·统考二模)如图1,∠1=55°,将矩形纸片沿虚线第一次折叠得到图2,再沿图2中的虚线进行第二次折叠得到图3(点O在MN上),则∠2的度数为 .
题型26 平行线的性质在实际生活的应用
1.(2023·河北石家庄·统考模拟预测)如图,烧杯内液体表面AB与烧杯下底部CD平行,光线EF从液体中射向空气时发生折射,光线变成FH,点G在射线EF上.已知∠HFB=20°,∠FED=56°,则∠GFH=( )
A.34°B.36°C.38°D.56°
2.(2022·山东济南·校考一模)图1是一款平板电脑文架,由托板、支撑板和底座构成.工作时,可将平板电脑吸附在托板上,底座放置在桌面上.图2是其侧面结构示意图,已知托板AB长200mm,支撑板CB长80mm,当∠ABC=130°,∠BCD=70°时,则托板顶点A到底座CD所在平面的距离为( )(结果精确到1mm).(参考数据:sin70°≈0.94,cs70°≈0.34,tan70°≈2.75,2≈1.41,3≈1.73).
A.246 mmB.247mmC.248mmD.249mm
3.(2022·浙江温州·统考三模)如图,在墙面上安装某一管道需经两次拐弯,拐弯后的管道与拐弯前的管道平行.若第一个弯道处∠B=140°,则第二个弯道处∠C也为140°,能解释这一现象的数学知识是( )
A.两直线平行,内错角相等.B.内错角相等,两直线平行.
C.两直线平行,同位角相等.D.同位角相等,两直线平行.
4.(2023·四川成都·统考二模)为测量校园某一块路线指示牌的高度,小明绘制了该指示牌支架侧面的截面图如图所示,并测得FG=1.3m,EF=1m,∠EFG=110°,∠AEF=70°,四边形ABCD为矩形底座,且AB=10cm.请帮助小明求出指示牌最高点G到地面BC的距离.(结果精确到1cm,参考数据:sin70°≈0.940,cs70°≈0.342,tan70°≈2.747,sin40°≈0.643,cs40°≈0.766,tan40°≈0.839)
题型26 利用平行线的性质解决三角板问题
1.(2022·福建福州·福建省福州第十九中学校考模拟预测)已知直线m∥n,将一块含45°角的直角三角板ABC按如图方式放置,其中斜边BC与直线n交于点D.若∠1=25°,则∠2的度数为( )
A.60°B.65°C.70°D.75°
2.(2023·河南·河南省实验中学校考三模)一副三角板如图所示摆放,∠BAC=∠DAE=90°,∠ACB=60°,∠AED=45°, BC∥DE,则∠BAD的度数为( )
A.15°B.20°C.25°D.30°
3.(2023下·广西南宁·七年级三美学校校考阶段练习)如图1,把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上.
(1)如图2,现把三角板绕B点逆时针旋转n°,当0
(3)如图1三角板ABC的放置,现将射线BF绕点B以每秒2°的转速逆时针旋转得到射线BM,同时射线QA绕点Q以每秒3°的转速顺时针旋转得到射线QN,当射线QN旋转至与QB重合时,则射线BM、QN均停止转动,设旋转时间为ts.在旋转过程中,是否存在BM∥QN若存在,求出此时t的值;若不存在,请说明理由.
题型27 根据平行线性质与判定求角度
1.(2023·江苏扬州·校联考二模)某同学制作简易工具来测量物体表面的倾斜程度,方法如下:将刻度重新设计的量角器固定在等腰直角三角板上,使量角器的90°刻度线与三角板的底边平行.将用细线和铅锤做成的重锤线顶端固定在五角器中心点O处,现将三角板底边紧贴被测物体表面,如图所示,此时重锤线在量角器:对应的刻度为32°,那么被测物体表面的倾斜角α为( )
A.24°B.32°C.36°D.58°
2.(2023·河南周口·校联考二模)已知一个零刻度落在点A的量角器(半圆O)的直径为AB,一等腰直角三角板绕点B旋转.
(1)如图1所示,当等腰直角三角板的斜边交半圆于C点,一直边交半圆于D点,另一直边交半圆于E点,若点C在量角器上的读数为25°,求此时点E在量角器上的读数;
(2)如图2所示,当点C、D在量角器上的读数α、β满足什么关系时,直角边与半圆O相切于点D
题型28 根据平行线性质与判定证明
1.(2023·河北秦皇岛·统考一模)如图,将一副直角三角板如图摆放,∠GEF=60°,∠MNP=45°,∠BEF=75°.
(1)AB与CD的位置关系是 ;
(2)在不标字母的情况下,找出与∠AEG相等的角是 .
2.(2019·广东中山·统考二模)将两块直角三角板如图1放置,等腰直角三角板ABC的直角顶点是点A,AB=AC=3,直角板EDF的直角顶点D在BC上,且CD:DB=1:2,∠F=30°.三角板ABC固定不动,将三角板EDF绕点D逆时针旋转,旋转角为α 0°<α<90°.
(1)当α=_______时,EF//BC;
(2)当α=45°时,三角板EDF绕点D逆时针旋转至如图2位置,设DF与AC交于点M,DE交AB于点N,求四边形ANDM的面积.
(3)如图3,设CM=x,四边形ANDM的面积为y,求y关于x的表达式(不用写x的取值范围).
3.(2021·江苏盐城·统考二模)如图,将一副斜边相等的直角三角板按斜边重合摆放在同一平面内,其中∠DAB=45°,∠CAB=30°,点O为斜边AB的中点,连接CD交AB于点E.设AB=1.
(1)求证:A、B、C、D四个点在以点O为圆心的同一个圆上;
(2)分别求△ABC和△ABD的面积;
(3)过点D作DF∥BC交AB于点F,求OE︰OF的比值.
1.(2022·河北·统考中考真题)①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③B.②③C.③④D.①④
2.(2023·吉林长春·统考中考真题)下图是一个多面体的表面展开图,每个面都标注了数字.若多面体的底面是面③,则多面体的上面是( )
A.面①B.面②C.面⑤D.面⑥
3.(2023·山东·统考中考真题)如图是一正方体的表面展开图.将其折叠成正方体后,与顶点K距离最远的顶点是( )
A.A点B.B点C.C点D.D点
4.(2023·山东青岛·统考中考真题)一个不透明小立方块的六个面上分别标有数字1,2,3,4,5,6,其展开图如图①所示.在一张不透明的桌子上,按图②方式将三个这样的小立方块搭成一个几何体,则该几何体能看得到的面上数字之和最小是( )
A.31B.32C.33D.34
5.(2022·浙江金华·统考中考真题)如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A.B.C.D.
6.(2022·江苏徐州·统考中考真题)如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A.B.C.D.
7.(2022·贵州六盘水·统考中考真题)如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是( )
A.①B.②C.③D.④
8.(2022·四川巴中·统考中考真题)七巧板是我国的一种传统智力玩具,下列用七巧板拼成的图形是轴对称图形的是( )
A.B.C.D.
9.(2022·广西柳州·统考中考真题)如图,从学校A到书店B有①、②、③、④四条路线,其中最短的路线是( )
A.①B.②C.③D.④
10.(2023·北京·统考中考真题)如图,∠AOC=∠BOD=90°,∠AOD=126°,则∠BOC的大小为( )
A.36°B.44°C.54°D.63°
11.(2023·河北·统考中考真题)淇淇一家要到革命圣地西柏坡参观.如图,西柏坡位于淇淇家南偏西70°的方向,则淇淇家位于西柏坡的( )
A.南偏西70°方向B.南偏东20°方向
C.北偏西20°方向D.北偏东70°方向
12.(2023·甘肃武威·统考中考真题)如图1,汉代初期的《淮南万毕术》是中国古代有关物理、化学的重要文献,书中记载了我国古代学者在科学领域做过的一些探索及成就.其中所记载的“取大镜高悬,置水盆于其下,则见四邻矣”,是古人利用光的反射定律改变光路的方法,即“反射光线与入射光线、法线在同一平面上;反射光线和入射光线位于法线的两侧;反射角等于人射角”.为了探清一口深井的底部情况,运用此原理,如图在井口放置一面平面镜可改变光路,当太阳光线AB与地面CD所成夹角∠ABC=50°时,要使太阳光线经反射后刚好垂直于地面射入深井底部,则需要调整平面镜EF与地面的夹角∠EBC=( )
A.60°B.70°C.80°D.85°
13.(2023·黑龙江绥化·统考中考真题)将一副三角板按下图所示摆放在一组平行线内,∠1=25°,∠2=30°,则∠3的度数为( )
A.55°B.65°C.70°D.75°
14.(2023·重庆·统考中考真题)如图,AB∥CD,AD⊥AC,若∠1=55°,则∠2的度数为( )
A.35°B.45°C.50°D.55°
15.(2023·广东深圳·统考中考真题)如图为商场某品牌椅子的侧面图,∠DEF=120°,DE与地面平行,∠ABD=50°,则∠ACB=( )
A.70°B.65°C.60°D.50°
16.(2023·江苏苏州·统考中考真题)如图,在正方形网格内,线段PQ的两个端点都在格点上,网格内另有A,B,C,D四个格点,下面四个结论中,正确的是( )
A.连接AB,则AB∥PQB.连接BC,则BC∥PQ
C.连接BD,则BD⊥PQD.连接AD,则AD⊥PQ
17.(2023·广东·统考中考真题)如图,街道AB与CD平行,拐角∠ABC=137°,则拐角∠BCD=( )
A.43°B.53°C.107°D.137°
18.(2023·山西·统考中考真题)如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P,点F为焦点.若∠1=155°,∠2=30°,则∠3的度数为( )
A.45°B.50°C.55°D.60°
19.(2023·湖北荆州·统考中考真题)如图所示的“箭头”图形中,AB∥CD,∠B=∠D=80∘,∠E=∠F=47∘,则图中∠G的度数是( )
A.80∘B.76∘C.66∘D.56∘
20.(2023·黑龙江大庆·统考中考真题)一个圆锥的底面半径为5,高为12,则它的体积为 .
21.(2023·湖南·统考中考真题)七巧板是我国民间广为流传的一种益智玩具,某同学用边长为4dm的正方形纸板制作了一副七巧板(如图),由5个等腰直角三角形,1个正方形和1个平行四边形组成.则图中阴影部分的面积为 dm3.
22.(2022·江西·统考中考真题)沐沐用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形(如图所示),则长方形的对角线长为 .
23.(2023·江西·统考中考真题)将含30°角的直角三角板和直尺按如图所示的方式放置,已∠α=60°,点B,C表示的刻度分别为1cm,3cm,则线段AB的长为 cm.
24.(2023·湖北十堰·统考中考真题)一副三角板按如图所示放置,点A在DE上,点F在BC上,若∠EAB=35°,则∠DFC= °.
25.(2023·湖南·统考中考真题)《周礼考工记》中记载有:“……半矩谓之宣(xuān),一宣有半谓之欘(zhú)……”意思是:“……直角的一半的角叫做宣,一宣半的角叫做欘……”.即:1宣=12矩,1欘=112宣(其中,1矩=90°),问题:图(1)为中国古代一种强弩图,图(2)为这种强弩图的部分组件的示意图,若∠A=1矩,∠B=1欘,则∠C= 度.
26.(2023·内蒙古通辽·统考中考真题)将一副三角尺如图所示放置,其中AB∥DE,则∠CDF= 度.
27.(2023·四川乐山·统考中考真题)如图,点O在直线AB上,OD是∠BOC的平分线,若∠AOC=140°,则∠BOD的度数为 .
28.(2023·浙江台州·统考中考真题)用一张等宽的纸条折成如图所示的图案,若∠1=20°,则∠2的度数为 .
29.(2023·湖北武汉·统考中考真题)如图,在四边形ABCD中,AD∥BC,∠B=∠D,点E在BA的延长线上,连接CE.
(1)求证:∠E=∠ECD;
(2)若∠E=60°,CE平分∠BCD,直接写出△BCE的形状.−3
2
a
c
b
−1
第28讲 与圆有关的计算(练习)2024年中考数学一轮复习(讲义+练习)(全国通用): 这是一份第28讲 与圆有关的计算(练习)2024年中考数学一轮复习(讲义+练习)(全国通用),文件包含第28讲与圆有关的计算练习原卷版docx、第28讲与圆有关的计算练习解析版docx等2份试卷配套教学资源,其中试卷共154页, 欢迎下载使用。
第15讲 几何图形的初步(讲义)2024年中考数学一轮复习(讲义+练习)(全国通用): 这是一份第15讲 几何图形的初步(讲义)2024年中考数学一轮复习(讲义+练习)(全国通用),文件包含第15讲几何图形的初步讲义原卷版docx、第15讲几何图形的初步讲义解析版docx等2份试卷配套教学资源,其中试卷共131页, 欢迎下载使用。
第28讲 与圆有关的计算(3考点+30题型)(讲义)-2024年中考数学一轮复习讲义+练习+测试(全国通用): 这是一份第28讲 与圆有关的计算(3考点+30题型)(讲义)-2024年中考数学一轮复习讲义+练习+测试(全国通用),文件包含第28讲与圆有关的计算讲义原卷版docx、第28讲与圆有关的计算讲义解析版docx等2份试卷配套教学资源,其中试卷共142页, 欢迎下载使用。












