


所属成套资源:2024年中考数学一轮复习讲练测(全国通用)
- 重难点04 二次函数中的平移、翻折、对称、旋转、折叠问题(5题型)-2024年中考数学一轮复习(全国通用) 试卷 6 次下载
- 重难点05 二次函数与几何的动点及最值、存在性问题(14题型)-2024年中考数学一轮复习(全国通用) 试卷 6 次下载
- 重难点07 三角形的6种模型(A字、8字、飞镖、老鹰抓小鸡、双角平分线模型、三角形折叠)-2024年中考数学一轮复习讲练测(全国通用) 试卷 1 次下载
- 重难点08 全等三角形8种模型(一线三等角、手拉手模型、倍长中线等)-2024年中考数学一轮复习讲义(全国通用) 学案 6 次下载
- 重难点09 相似三角形8种模型(A字、8字、射影定理、一线三等角等)-2024年中考数学一轮复习讲义(全国通用) 学案 6 次下载
重难点06 相交线与平行线的5种模型(5题型)-2024年中考数学一轮复习(全国通用)
展开
这是一份重难点06 相交线与平行线的5种模型(5题型)-2024年中考数学一轮复习(全国通用),文件包含重难点突破06相交线与平行线的5种模型三线八角铅笔头锯齿型翘脚三角板拼接型原卷版docx、重难点突破06相交线与平行线的5种模型三线八角铅笔头锯齿型翘脚三角板拼接型解析版docx等2份试卷配套教学资源,其中试卷共49页, 欢迎下载使用。
2、学会运用数形结合思想。数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系,寻求代数问题的解决方法(以形助数),或利用数量关系来研究几何图形的性质,解决几何问题(以数助形)的一种数学思想。
3、要学会抢得分点。一道中考数学压轴题解不出来,不等于“一点不懂、一点不会”,要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。在研究数学问题时,我们通常是将未知问题转化为已知的问题,将复杂的问题转化为简单的问题,将抽象的问题转化为具体的问题,将实际问题转化为数学问题。
5、学会运用分类讨论的思想。如果不注意对各种情况分类讨论,就有可能造成错解或漏解,纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想:体现在数学上也就是要把难的问题转化为简单的问题,把不熟悉的问题转化为熟悉的问题,把未知的问题转化为已知的问题。
重难点突破06 相交线与平行线的5种模型
(三线八角、铅笔头、锯齿型、翘脚、三角板拼接模型)
目 录
TOC \ "1-3" \n \h \z \u
\l "_Tc155795834" 题型01 三线八角模型
\l "_Tc155795835" 题型02 铅笔头模型
\l "_Tc155795836" 题型03 锯齿型模型
\l "_Tc155795837" 题型04 翘脚模型
\l "_Tc155795838" 题型05 三角板拼接模型
题型01 三线八角模型
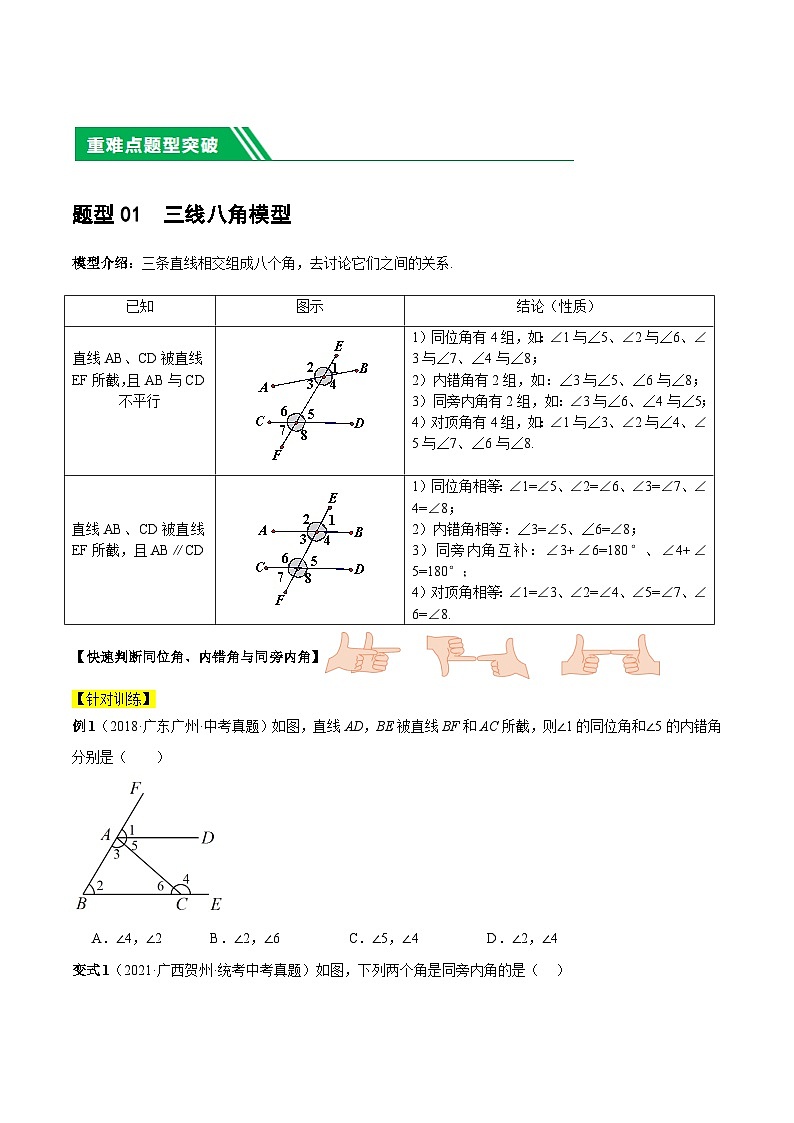
模型介绍:三条直线相交组成八个角,去讨论它们之间的关系.
【快速判断同位角、内错角与同旁内角】
【针对训练】
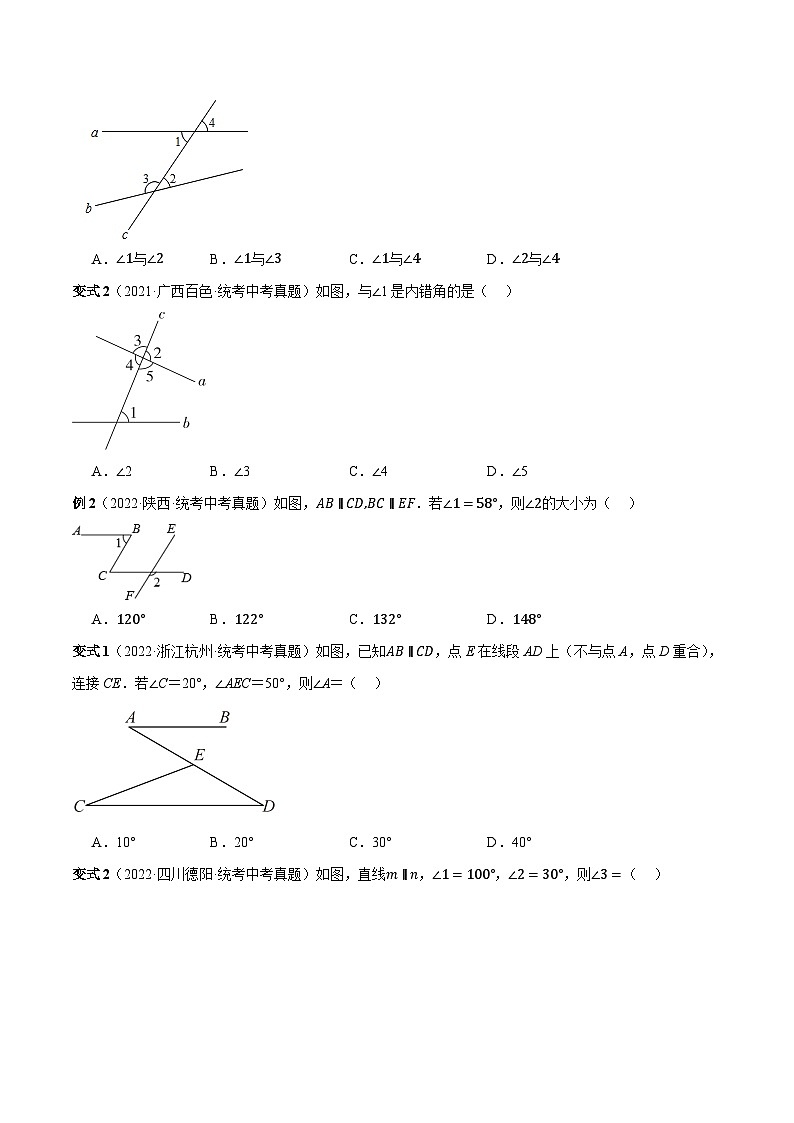
例1(2018·广东广州·中考真题)如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( )
A.∠4,∠2B.∠2,∠6C.∠5,∠4D.∠2,∠4
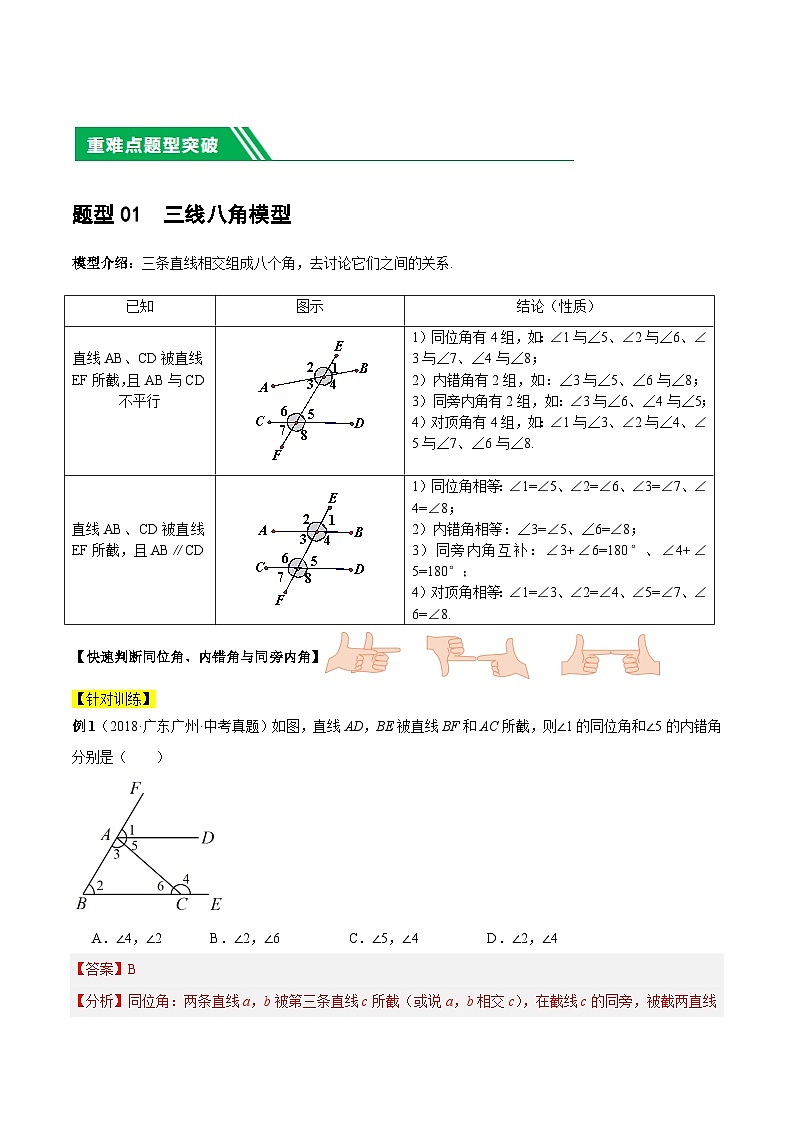
变式1(2021·广西贺州·统考中考真题)如图,下列两个角是同旁内角的是( )
A.∠1与∠2B.∠1与∠3C.∠1与∠4D.∠2与∠4
变式2(2021·广西百色·统考中考真题)如图,与∠1是内错角的是( )
A.∠2B.∠3C.∠4D.∠5
例2(2022·陕西·统考中考真题)如图,AB∥CD,BC∥EF.若∠1=58°,则∠2的大小为( )
A.120°B.122°C.132°D.148°
变式1(2022·浙江杭州·统考中考真题)如图,已知AB∥CD,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10°B.20°C.30°D.40°
变式2(2022·四川德阳·统考中考真题)如图,直线m∥n,∠1=100°,∠2=30°,则∠3=( )
A.70°B.110°C.130°D.150°
变式3(2022·辽宁·统考中考真题)如图,直线m∥n,AC⊥BC于点C,∠1=30°,则∠2的度数为( )
A.140°B.130°C.120°D.110°
题型02 铅笔头模型
【针对训练】
例3如图,已知:AB∥CD,求证:∠PAB+∠APC+∠PCD=360°.
变式1如图,如果AB∥CD,那么∠B+∠F+∠E+∠D= °.
变式2 问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
思路点拨:
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可分别求出∠APE、∠CPE的度数,从而可求出∠APC的度数;
小丽的思路是:如图3,连接AC,通过平行线性质以及三角形内角和的知识可求出∠APC的度数;
小芳的思路是:如图4,延长AP交DC的延长线于E,通过平行线性质以及三角形外角的相关知识可求出∠APC的度数.
问题解决:请从小明、小丽、小芳的思路中任选一种思路进行推理计算,你求得的∠APC的度数为 °;
问题迁移:
(1)如图5,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
变式3 如图,已知AB∥CD.
(1)如图1所示,∠1+∠2= ;
(2)如图2所示,∠1+∠2+∠3= ;并写出求解过程.
(3)如图3所示,∠1+∠2+∠3+∠4= ;
(4)如图4所示,试探究∠1+∠2+∠3+∠4+⋯+∠n= .
变式4(1)如图1,l1∥l2,求∠A1+∠A2+∠A3=______.(直接写出结果)
(2)如图2,l1∥l2,求∠A1+∠A2+∠A3+∠A4=_____.(直接写出结果)
(3)如图3,l1∥l2,求∠A1+∠A2+∠A3+∠A4+∠A5=_______.(直接写出结果)
(4)如图4,l1∥l2,求∠A1+∠A2+…+∠An=_______.(直接写出结果)
题型03 锯齿型模型
【针对训练】
例4(2020·湖南·中考真题)如图,已知AB∥DE,∠1=30°,∠2=35°,则∠BCE的度数为( )
A.70°B.65°C.35°D.5°
变式1(2023·北京西城·统考一模)下面是解答一道几何题时两种添加辅助线的方法,选择其中一种,完成证明.
变式2(2023·甘肃陇南·校考一模)如图,直线AB∥CD,∠EFG−∠AEF=30°,则∠FGD= .
变式3 问题情境:如图1,已知AB∥CD,∠APC=108°.求∠PAB+∠PCD的度数.
经过思考,小敏的思路是:如图2,过P作PE∥AB,根据平行线有关性质,可得∠PAB+∠PCD=360°−∠APC=252°.
问题迁移:如图3,AD∥BC,点P在射线OM上运动, ∠ADP=∠α,∠BCP=∠β.
(1)当点P在A、B两点之间运动时, ∠CPD、∠α、∠β之间有何数量关系?请说明理由.
(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.
(3)问题拓展:如图4,MA1∥NAn,A1−B1−A2−⋯−Bn−1−An是一条折线段,依据此图所含信息,把你所发现的结论,用简洁的数学式子表达为 .
变式4.如图1,四边形为一张长方形纸片.
(1)如图2,将长方形纸片剪两刀,剪出三个角(),则__________°.
(2)如图3,将长方形纸片剪三刀,剪出四个角(),则__________°.
(3)如图4,将长方形纸片剪四刀,剪出五个角(),则___________°.
(4)根据前面探索出的规律,将本题按照上述剪法剪刀,剪出个角,那么这个角的和是____________°.
变式5(1)如图1,AM∥CN,求证:
①∠MAB+∠ABC+∠BCN=360°;
②∠MAE+∠AEF+∠EFC+∠FCN=540°;
(2)如图2,若平行线AM与CN间有n个点,根据(1)中的结论写出你的猜想并证明.
题型04 翘脚模型
【针对训练】
例5(2023·重庆大渡口·统考模拟预测)在数学课上老师提出了如下问题:
如图,∠B=160°,当∠A与∠D满足什么关系时,BC∥DE?
小明认为∠D−∠A=20°时BC∥DE,他解答这个问题的思路和步骤如下,请根据小明的思路完成下面的作图与填空:
解:用直尺和圆规,在DA的右侧找一点M,使∠DAM=∠D(只保留作图痕迹).
∵∠DAM=∠D,
∴①_____________
∵∠D−∠DAB=20°
∴∠BAM=②_________°,
∵∠B=160°,
∴∠B+∠BAM=③__________°,
∴④_____________
∴BC∥DE.
所以满足的关系为:当∠D−∠A=20°时,BC∥DE.
变式1(2023·云南·校考一模)如图,AB∥CD,∠A=30°,∠C=70°,则∠F= °.
变式2(2021·全国·九年级专题练习)如图,如果AB∥EF,EF∥CD,则∠1,∠2,∠3的关系式 .
变式3 ①如图1,,则;②如图2,,则;③如图3,,则;④如图4,直线 EF,点在直线上,则.以上结论正确的个数是( )
A.1个B.2个C.3个D.4个
变式4.①如图1,ABCD,则∠A+∠E+∠C=180°;②如图2,ABCD,则∠E=∠A+∠C;③如图3,ABCD,则∠A+∠E-∠1=180°;④如图4,ABCD,则∠A=∠C+∠P.以上结论正确的个数是( )
A.①②③④B.①②③C.②③④D.①②④
变式5.已知直线AB∥CD,P为平面内一点,连接PA、PD.
(1)如图1,已知∠A=50°,∠D=150°,求∠APD的度数;
(2)如图2,判断∠PAB、∠CDP、∠APD之间的数量关系为 .
(3)如图3,在(2)的条件下,AP⊥PD,DN平分∠PDC,若∠PAN+∠PAB=∠APD,求∠AND的度数.
题型05 三角板拼接模型
【解题方法】通过一副三角板我们能拼出以下特殊角,如:60°、75°、90°,依据平行线的性质,我们可以得到同位角、内错角、同旁内角之间的关系,从而求出对应角度数..
【针对训练】
例6(2022·广东深圳·统考中考真题)将一副三角板如图所示放置,斜边平行,则∠1的度数为( )
A.5°B.10°C.15°D.20°
变式1(2022·江苏扬州·统考中考真题)将一副直角三角板如图放置,已知∠E=60°,∠C=45°,EF∥BC,则∠BND= °.
变式2(2021·湖北宜昌·统考中考真题)如图,将一副三角尺按图中所示位置摆放,点F在AC上,其中∠ACB=90°,∠ABC=60°,∠EFD=90°,∠DEF=45°,AB//DE,则∠AFD的度数是( )
A.15°B.30°C.45°D.60°
变式3(2021·贵州黔西·中考真题)将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.95°B.100°C.105°D.110°
变式4(2022·山东淄博·统考一模)一副三角板按如图所示叠放,其中∠ACB=∠DCE=90°,∠A=30°,∠D=45°,且AC∥DE,则∠BCD= 度.
变式5.(2022·江苏镇江中考真题)一副三角板如图放置,∠A=45°,∠E=30°,DE∥AC,则∠1=
变式6(2023·福建厦门·厦门市第十一中学校考二模)一副三角板如图方式摆放,点D在直线EF上,且AB//EF,则∠ADE= 度.
变式7(2023·浙江温州·校考三模)一副直角三角板如图放置,点E在边BC的延长线上,BE∥DF,∠B=∠DEF=90°,则∠CDE的度数为 .
已知
图示
结论(性质)
直线AB、CD被直线EF所截,且AB与CD不平行
1)同位角有4组,如:∠1与∠5、∠2与∠6、∠3与∠7、∠4与∠8;
2)内错角有2组,如:∠3与∠5、∠6与∠8;
3)同旁内角有2组,如:∠3与∠6、∠4与∠5;
4)对顶角有4组,如:∠1与∠3、∠2与∠4、∠5与∠7、∠6与∠8.
直线AB、CD被直线EF所截,且AB∥CD
1)同位角相等:∠1=∠5、∠2=∠6、∠3=∠7、∠4=∠8;
2)内错角相等:∠3=∠5、∠6=∠8;
3)同旁内角互补:∠3+∠6=180°、∠4+∠5=180°;
4)对顶角相等:∠1=∠3、∠2=∠4、∠5=∠7、∠6=∠8.
已知
图示
结论(性质)
证明方法
AB∥DE
∠B+∠C+∠E = 360°
遇拐点做平行线(方法不唯一)
AB∥DE
∠B+∠M+∠N+∠E= 540°
a∥b
∠A1+∠A2+...+∠An-1+∠An=180°×(n-1)=180°×(拐点数+1)
已知
图示
结论(性质)
证明方法
AB∥DE
∠B+∠E=∠C
遇拐点做平行线(方法不唯一)
AB∥DE
∠B+∠M+∠E=∠C+∠N
a∥b
所有朝左角之和等于所有朝右角的和
已知:如图,AB∥CD.
求证:∠AEC=∠A+∠C
方法一
证明:如图,过点E作MN∥AB
方法二
证明:如图,延长AE,交CD于点F.
已知
图示
结论(性质)
证明方法
AB∥DE
∠1=∠2+∠3
遇拐点做平行线(方法不唯一)
AB∥DE
∠1+∠3-∠2=180°
相关试卷
这是一份专题06 对角互补模型在三角形中应用-中考数学重难点专项突破(全国通用),共6页。
这是一份专题06 对角互补模型在三角形中应用(提升训练)-中考数学重难点专项突破(全国通用),文件包含专题06对角互补模型在三角形中应用提升训练原卷版docx、专题06对角互补模型在三角形中应用提升训练解析版docx等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。
这是一份重难点06 相交线与平行线的5种模型(三线八角、铅笔头、锯齿型、翘脚、三角板拼接型)(5题型)-备战2024年中考数学一轮复习高效讲练测(全国通用),文件包含重难点突破06相交线与平行线的5种模型三线八角铅笔头锯齿型翘脚三角板拼接型原卷版docx、重难点突破06相交线与平行线的5种模型三线八角铅笔头锯齿型翘脚三角板拼接型解析版docx等2份试卷配套教学资源,其中试卷共49页, 欢迎下载使用。








