
所属成套资源:2021-2023年高考数学真题分类汇编(全国通用)专题特训
2021-2023年高考数学真题分类汇编(全国通用)专题14概率与统计(选择题、填空题)(理)(学生版+解析)
展开这是一份2021-2023年高考数学真题分类汇编(全国通用)专题14概率与统计(选择题、填空题)(理)(学生版+解析),共20页。
知识点2:条件概率
知识点3:信息图表处理
知识点4:频率分布直方图
知识点5:概率最值问题
知识点6:古典概型
知识点7:正态分布与相互独立
知识点8:平均数、中位数、众数、方差、标准差、极差
知识点9:概率综合问题
近三年高考真题
知识点1:回归分析
1.(2023•天津)调查某种花萼长度和花瓣长度,所得数据如图所示,其中相关系数,下列说法正确的是
A.花瓣长度和花萼长度没有相关性
B.花瓣长度和花萼长度呈现负相关
C.花瓣长度和花萼长度呈现正相关
D.若从样本中抽取一部分,则这部分的相关系数一定是0.8245
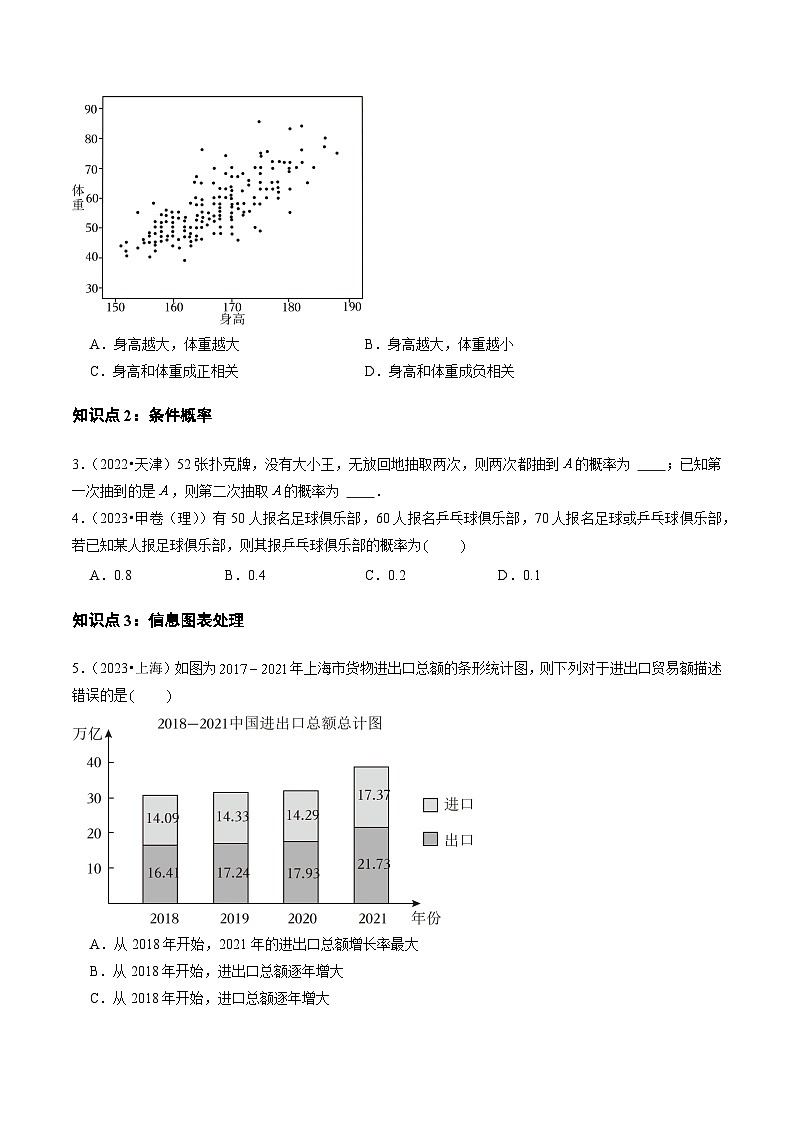
2.(2023•上海)根据所示的散点图,下列说法正确的是
A.身高越大,体重越大B.身高越大,体重越小
C.身高和体重成正相关D.身高和体重成负相关
知识点2:条件概率
3.(2022•天津)52张扑克牌,没有大小王,无放回地抽取两次,则两次都抽到的概率为 ;已知第一次抽到的是,则第二次抽取的概率为 .
4.(2023•甲卷(理))有50人报名足球俱乐部,60人报名乒乓球俱乐部,70人报名足球或乒乓球俱乐部,若已知某人报足球俱乐部,则其报乒乓球俱乐部的概率为
A.0.8B.0.4C.0.2D.0.1
知识点3:信息图表处理
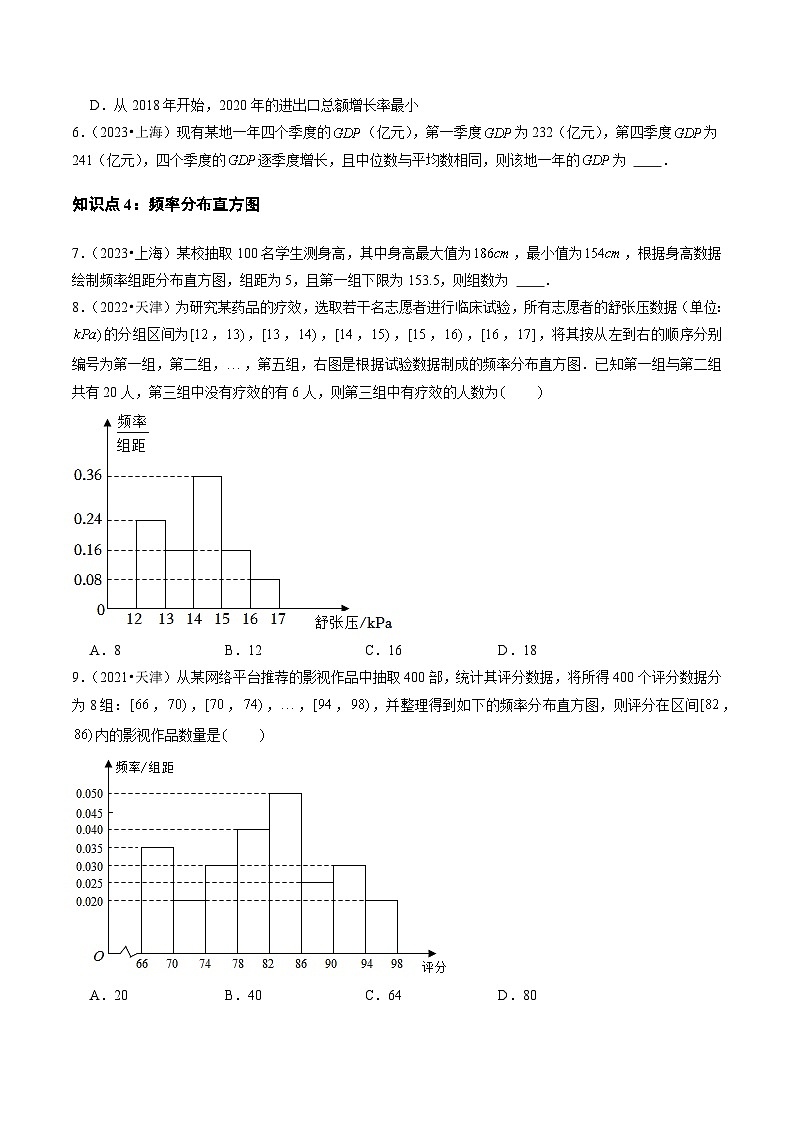
5.(2023•上海)如图为年上海市货物进出口总额的条形统计图,则下列对于进出口贸易额描述错误的是
A.从2018年开始,2021年的进出口总额增长率最大
B.从2018年开始,进出口总额逐年增大
C.从2018年开始,进口总额逐年增大
D.从2018年开始,2020年的进出口总额增长率最小
6.(2023•上海)现有某地一年四个季度的(亿元),第一季度为232(亿元),第四季度为241(亿元),四个季度的逐季度增长,且中位数与平均数相同,则该地一年的为 .
知识点4:频率分布直方图
7.(2023•上海)某校抽取100名学生测身高,其中身高最大值为,最小值为,根据身高数据绘制频率组距分布直方图,组距为5,且第一组下限为153.5,则组数为 .
8.(2022•天津)为研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:的分组区间为,,,,,,,,,,将其按从左到右的顺序分别编号为第一组,第二组,,第五组,右图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为
A.8B.12C.16D.18
9.(2021•天津)从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:,,,,,,,并整理得到如下的频率分布直方图,则评分在区间,内的影视作品数量是
A.20B.40C.64D.80
知识点5:概率最值问题
10.(2022•乙卷(理))某棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、乙、丙比赛获胜的概率分别为,,,且.记该棋手连胜两盘的概率为,则
A.与该棋手和甲、乙、丙的比赛次序无关
B.该棋手在第二盘与甲比赛,最大
C.该棋手在第二盘与乙比赛,最大
D.该棋手在第二盘与丙比赛,最大
知识点6:古典概型
11.(2023•上海)为了学习宣传党的二十大精神,某校学生理论宣讲团赴社区宣讲,已知有4名男生,6名女生,从10人中任选3人,则恰有1名男生2名女生的概率为 .
12.(2022•上海)为了检测学生的身体素质指标,从游泳类1项,球类3项,田径类4项共8项项目中随机抽取4项进行检测,则每一类都被抽到的概率为 .
13.(2022•甲卷(理))从正方体的8个顶点中任选4个,则这4个点在同一个平面的概率为 .
14.(2021•上海)已知花博会有四个不同的场馆,,,,甲、乙两人每人选2个去参观,则他们的选择中,恰有一个馆相同的概率为 .
15.(2022•新高考Ⅰ)从2至8的7个整数中随机取2个不同的数,则这2个数互质的概率为
A.B.C.D.
16.(2023•天津)甲、乙、丙三个盒子中装有一定数量的黑球和白球,其总数之比为.这三个盒子中黑球占总数的比例分别为,,.现从三个盒子中各取一个球,取到的三个球都是黑球的概率为 ;将三个盒子混合后任取一个球,是白球的概率为 .
17.(2021•全国)3位男同学与3位女同学随机排成一行,其中两端都不是女同学的概率为
A.B.C.D.
18.(2021•甲卷(理))将4个1和2个0随机排成一行,则2个0不相邻的概率为
A.B.C.D.
知识点7:正态分布与相互独立
19.(2021•新高考Ⅱ)某物理量的测量结果服从正态分布,则下列结论中不正确的是
A.越小,该物理量在一次测量中落在内的概率越大
B.该物理量在一次测量中大于10的概率为0.5
C.该物理量在一次测量中小于9.99与大于10.01的概率相等
D.该物理量在一次测量中结果落在与落在的概率相等
20.(2021•新高考Ⅰ)有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则
A.甲与丙相互独立B.甲与丁相互独立
C.乙与丙相互独立D.丙与丁相互独立
知识点8:平均数、中位数、众数、方差、标准差、极差
21.(多选题)(2023•新高考Ⅰ)有一组样本数据,,,,其中是最小值,是最大值,则
A.,,,的平均数等于,,,的平均数
B.,,,的中位数等于,,,的中位数
C.,,,的标准差不小于,,,的标准差
D.,,,的极差不大于,,,的极差
22.(多选题)(2021•新高考Ⅱ)下列统计量中,能度量样本,,,的离散程度的有
A.样本,,,的标准差B.样本,,,的中位数
C.样本,,,的极差D.样本,,,的平均数
23.(多选题)(2021•新高考Ⅰ)有一组样本数据,,,,由这组数据得到新样本数据,,,,其中,2,,,为非零常数,则
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样本数据的样本极差相同
知识点9:概率综合问题
24.(多选题)(2023•新高考Ⅱ)在信道内传输0,1信号,信号的传输相互独立.发送0时,收到1的概率为,收到0的概率为;发送1时,收到0的概率为,收到1的概率为.考虑两种传输方案:单次传输和三次传输.单次传输是指每个信号只发送1次,三次传输是指每个信号重复发送3次.收到的信号需要译码,译码规则如下:单次传输时,收到的信号即为译码;三次传输时,收到的信号中出现次数多的即为译码(例如,若依次收到1,0,1,则译码为
A.采用单次传输方案,若依次发送1,0,1,则依次收到1,0,1的概率为
B.采用三次传输方案,若发送1,则依次收到1,0,1的概率为
C.采用三次传输方案,若发送1,则译码为1的概率为
D.当时,若发送0,则采用三次传输方案译码为0的概率大于采用单次传输方案译码为0的概率
25.(2022•浙江)现有7张卡片,分别写上数字1,2,2,3,4,5,6.从这7张卡片中随机抽取3张,记所抽取卡片上数字的最小值为,则 , .
26.(2022•新高考Ⅱ)已知随机变量服从正态分布,且,则 .
27.(2021•天津)甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次平局.已知每次活动中,甲、乙猜对的概率分别为和,且每次活动中甲、乙猜对与否互不影响,各次活动也互不影响,则一次活动中,甲获胜的概率为 ;3次活动中,甲至少获胜2次的概率为 .
28.(2021•浙江)袋中有4个红球,个黄球,个绿球.现从中任取两个球,记取出的红球数为,若取出的两个球都是红球的概率为,一红一黄的概率为,则 , .
专题14 概率与统计(选择题、填空题)(理)
知识点目录
知识点1:回归分析
知识点2:条件概率
知识点3:信息图表处理
知识点4:频率分布直方图
知识点5:概率最值问题
知识点6:古典概型
知识点7:正态分布与相互独立
知识点8:平均数、中位数、众数、方差、标准差、极差
知识点9:概率综合问题
近三年高考真题
知识点1:回归分析
1.(2023•天津)调查某种花萼长度和花瓣长度,所得数据如图所示,其中相关系数,下列说法正确的是
A.花瓣长度和花萼长度没有相关性
B.花瓣长度和花萼长度呈现负相关
C.花瓣长度和花萼长度呈现正相关
D.若从样本中抽取一部分,则这部分的相关系数一定是0.8245
【答案】
【解析】相关系数,且散点图呈左下角到右上角的带状分布,
花瓣长度和花萼长度呈正相关.
若从样本中抽取一部分,则这部分的相关系数不一定是0.8245.
故选:.
2.(2023•上海)根据所示的散点图,下列说法正确的是
A.身高越大,体重越大B.身高越大,体重越小
C.身高和体重成正相关D.身高和体重成负相关
【答案】
【解析】根据散点图的分布可得:身高和体重成正相关.
故选:.
知识点2:条件概率
3.(2022•天津)52张扑克牌,没有大小王,无放回地抽取两次,则两次都抽到的概率为 ;已知第一次抽到的是,则第二次抽取的概率为 .
【答案】;.
【解析】由题意,设第一次抽到的事件为,第二次抽到的事件为,
则,(B),
,
故答案为:;.
4.(2023•甲卷(理))有50人报名足球俱乐部,60人报名乒乓球俱乐部,70人报名足球或乒乓球俱乐部,若已知某人报足球俱乐部,则其报乒乓球俱乐部的概率为
A.0.8B.0.4C.0.2D.0.1
【答案】
【解析】根据题意,在报名足球或乒乓球俱乐部的70人中,设某人报足球俱乐部为事件,报乒乓球俱乐部为事件,
则(A),
由于有50人报名足球俱乐部,60人报名乒乓球俱乐部,则同时报名两个俱乐部的由人,则,
则.
故选:.
知识点3:信息图表处理
5.(2023•上海)如图为年上海市货物进出口总额的条形统计图,则下列对于进出口贸易额描述错误的是
A.从2018年开始,2021年的进出口总额增长率最大
B.从2018年开始,进出口总额逐年增大
C.从2018年开始,进口总额逐年增大
D.从2018年开始,2020年的进出口总额增长率最小
【答案】
【解析】显然2021年相对于2020年进出口额增量增加特别明显,故最后一年的增长率最大,对;
统计图中的每一年条形图的高度逐年增加,故对;
2020年相对于2019的进口总额是减少的,故错;
显然进出口总额2021年的增长率最大,而2020年相对于2019年的增量比2019年相对于2018年的增量小,
且计算增长率时前者的分母还大,故2020年的增长率一定最小,正确.
故选:.
6.(2023•上海)现有某地一年四个季度的(亿元),第一季度为232(亿元),第四季度为241(亿元),四个季度的逐季度增长,且中位数与平均数相同,则该地一年的为 .
【答案】946(亿元).
【解析】设第二季度为亿元,第三季度为亿元,则,
中位数与平均数相同,
,
,
该地一年的为(亿元).
故答案为:946(亿元).
知识点4:频率分布直方图
7.(2023•上海)某校抽取100名学生测身高,其中身高最大值为,最小值为,根据身高数据绘制频率组距分布直方图,组距为5,且第一组下限为153.5,则组数为 .
【答案】7.
【解析】极差为,组距为5,且第一组下限为153.5,
,故组数为7组,
故答案为:7.
8.(2022•天津)为研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:的分组区间为,,,,,,,,,,将其按从左到右的顺序分别编号为第一组,第二组,,第五组,右图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为
A.8B.12C.16D.18
【答案】
【解析】志愿者的总人数为,
第3组的人数为,
有疗效的人数为人.
故选:.
9.(2021•天津)从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:,,,,,,,并整理得到如下的频率分布直方图,则评分在区间,内的影视作品数量是
A.20B.40C.64D.80
【答案】
【解析】由频率分布直方图知,
评分在区间,内的影视作品的频率为,
故评分在区间,内的影视作品数量是,
故选:.
知识点5:概率最值问题
10.(2022•乙卷(理))某棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、乙、丙比赛获胜的概率分别为,,,且.记该棋手连胜两盘的概率为,则
A.与该棋手和甲、乙、丙的比赛次序无关
B.该棋手在第二盘与甲比赛,最大
C.该棋手在第二盘与乙比赛,最大
D.该棋手在第二盘与丙比赛,最大
【答案】
【解析】选项,已知棋手与甲、乙、丙比赛获胜的概率不相等,所以受比赛次序影响,故错误;
设棋手在第二盘与甲比赛连赢两盘的概率为,棋手在第二盘与乙比赛连赢两盘的概率为,棋手在第二盘与丙比赛连赢两盘的概率为,
,
同理可得,,
,
,,
最大,即棋手在第二盘与丙比赛连赢两盘的概率最大.
故选:.
知识点6:古典概型
11.(2023•上海)为了学习宣传党的二十大精神,某校学生理论宣讲团赴社区宣讲,已知有4名男生,6名女生,从10人中任选3人,则恰有1名男生2名女生的概率为 .
【答案】0.5.
【解析】从10人中任选3人的事件个数为,
恰有1名男生2名女生的事件个数为,
则恰有1名男生2名女生的概率为.
故答案为:0.5.
12.(2022•上海)为了检测学生的身体素质指标,从游泳类1项,球类3项,田径类4项共8项项目中随机抽取4项进行检测,则每一类都被抽到的概率为 .
【答案】.
【解析】从游泳类1项,球类3项,田径类4项共8项项目中随机抽取4项进行检测,
则每一类都被抽到的方法共有种,
而所有的抽取方法共有种,
故每一类都被抽到的概率为,
故答案为:.
13.(2022•甲卷(理))从正方体的8个顶点中任选4个,则这4个点在同一个平面的概率为 .
【答案】.
【解析】根据题意,从正方体的8个顶点中任选4个,有种取法,
若这4个点在同一个平面,有底面2个和侧面4个、对角面6个,一共有12种情况,
则这4个点在同一个平面的概率;
故答案为:.
14.(2021•上海)已知花博会有四个不同的场馆,,,,甲、乙两人每人选2个去参观,则他们的选择中,恰有一个馆相同的概率为 .
【答案】.
【解析】甲选2个去参观,有种,乙选2个去参观,有种,共有种,
若甲乙恰有一个馆相同,则选确定相同的馆有种,然后从剩余3个馆种选2个进行排列,有种,共有种,
则对应概率,
故答案为:.
15.(2022•新高考Ⅰ)从2至8的7个整数中随机取2个不同的数,则这2个数互质的概率为
A.B.C.D.
【答案】
【解析】从2至8的7个整数中任取两个数共有种方式,
其中互质的有:23,25,27,34,35,37,38,45,47,56,57,58,67,78,共14种,
故所求概率为.
故选:.
16.(2023•天津)甲、乙、丙三个盒子中装有一定数量的黑球和白球,其总数之比为.这三个盒子中黑球占总数的比例分别为,,.现从三个盒子中各取一个球,取到的三个球都是黑球的概率为 ;将三个盒子混合后任取一个球,是白球的概率为 .
【答案】;.
【解析】设盒子中共有球个,
则甲盒子中有黑球个,白球个,
乙盒子中有黑球个,白球个,
丙盒子中有黑球个,白球个,
从三个盒子中各取一个球,取到的三个球都是黑球的概率为;
将三个盒子混合后任取一个球,是白球的概率.
故答案为:;.
17.(2021•全国)3位男同学与3位女同学随机排成一行,其中两端都不是女同学的概率为
A.B.C.D.
【答案】
【解析】3位男同学与3位女同学随机排成一行,排法总数,
其中两端都不是女同学的排法种数为,
则其中两端都不是女同学的概率为.
故选:.
18.(2021•甲卷(理))将4个1和2个0随机排成一行,则2个0不相邻的概率为
A.B.C.D.
【答案】
【解析】6个空位选2两个放0,剩余4个放1,故总的排放方法有种,
利用插空法,4个1有5个位置可以放0,故排放方法有种,
所以所求概率为.
故选:.
知识点7:正态分布与相互独立
19.(2021•新高考Ⅱ)某物理量的测量结果服从正态分布,则下列结论中不正确的是
A.越小,该物理量在一次测量中落在内的概率越大
B.该物理量在一次测量中大于10的概率为0.5
C.该物理量在一次测量中小于9.99与大于10.01的概率相等
D.该物理量在一次测量中结果落在与落在的概率相等
【答案】
【解析】因为某物理量的测量结果服从正态分布,
所以测量的结果的概率分布关于10对称,且方差越小,则分布越集中,
对于,越小,概率越集中在10左右,则该物理量一次测量结果落在内的概率越大,故选项正确;
对于,测量结果大于10的概率为0.5,故选项正确;
对于,由于概率分布关于10对称,所以测量结果大于10.01的概率等于小于9.99的概率,故选项正确;
对于,由于概率分布是集中在10附近的,分布在10附近的区域大于分布在10附近的区域,
故测量结果落在内的概率大于落在内的概率,故选项错误.
故选:.
20.(2021•新高考Ⅰ)有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则
A.甲与丙相互独立B.甲与丁相互独立
C.乙与丙相互独立D.丙与丁相互独立
【答案】
【解析】由题意可知,两点数和为8的所有可能为:,,,,,
两点数和为7的所有可能为,,,,,,
(甲,(乙,(丙,(丁,
(甲丙)(甲(丙,
(甲丁)(甲(丁,
(乙丙)(乙(丙,
(丙丁)(丙(丁,
故选:.
知识点8:平均数、中位数、众数、方差、标准差、极差
21.(多选题)(2023•新高考Ⅰ)有一组样本数据,,,,其中是最小值,是最大值,则
A.,,,的平均数等于,,,的平均数
B.,,,的中位数等于,,,的中位数
C.,,,的标准差不小于,,,的标准差
D.,,,的极差不大于,,,的极差
【答案】
【解析】选项,,,,的平均数不一定等于,,,的平均数,错误;
选项,,,,的中位数等于,,,,的中位数等于,正确;
选项,设样本数据,,,为0,1,2,8,9,10,可知,,,的平均数是5,,,,的平均数是5,
,,,的方差,
,,,的方差,
,,错误.
选项,,,,正确.
故选:.
22.(多选题)(2021•新高考Ⅱ)下列统计量中,能度量样本,,,的离散程度的有
A.样本,,,的标准差B.样本,,,的中位数
C.样本,,,的极差D.样本,,,的平均数
【答案】
【解析】中位数是反应数据的变化,
方差是反应数据与均值之间的偏离程度,
极差是用来表示统计资料中的变异量数,反映的是最大值与最小值之间的差距,
平均数是反应数据的平均水平,
故能反应一组数据离散程度的是标准差,极差.
故选:.
23.(多选题)(2021•新高考Ⅰ)有一组样本数据,,,,由这组数据得到新样本数据,,,,其中,2,,,为非零常数,则
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样本数据的样本极差相同
【答案】
【解析】对于,两组数据的平均数的差为,故错误;
对于,两组样本数据的样本中位数的差是,故错误;
对于,标准差,
两组样本数据的样本标准差相同,故正确;
对于,,2,,,为非零常数,
的极差为,的极差为,
两组样本数据的样本极差相同,故正确.
故选:.
知识点9:概率综合问题
24.(多选题)(2023•新高考Ⅱ)在信道内传输0,1信号,信号的传输相互独立.发送0时,收到1的概率为,收到0的概率为;发送1时,收到0的概率为,收到1的概率为.考虑两种传输方案:单次传输和三次传输.单次传输是指每个信号只发送1次,三次传输是指每个信号重复发送3次.收到的信号需要译码,译码规则如下:单次传输时,收到的信号即为译码;三次传输时,收到的信号中出现次数多的即为译码(例如,若依次收到1,0,1,则译码为
A.采用单次传输方案,若依次发送1,0,1,则依次收到1,0,1的概率为
B.采用三次传输方案,若发送1,则依次收到1,0,1的概率为
C.采用三次传输方案,若发送1,则译码为1的概率为
D.当时,若发送0,则采用三次传输方案译码为0的概率大于采用单次传输方案译码为0的概率
【答案】
【解析】采用单次传输方案,若依次发送1,0,1,则依次收到1,0,1的概率为:,故正确;
采用三次传输方案,若发送1,依次收到1,0,1的概率为:,故正确;
采用三次传输方案,若发送1,
则译码为1包含收到的信号为包含两个1或3个1,
故所求概率为:,故错误;
三次传输方案发送0,译码为0的概率,
单次传输发送0译码为0的概率,
,
当时,,
故,故正确.
故选:.
25.(2022•浙江)现有7张卡片,分别写上数字1,2,2,3,4,5,6.从这7张卡片中随机抽取3张,记所抽取卡片上数字的最小值为,则 , .
【答案】;.
【解析】根据题意可得:的取值可为1,2,3,4,
又,
,
,
,
,
故答案为:;.
26.(2022•新高考Ⅱ)已知随机变量服从正态分布,且,则 .
【答案】0.14.
【解析】随机变量服从正态分布,
,
,
故答案为:0.14.
27.(2021•天津)甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次平局.已知每次活动中,甲、乙猜对的概率分别为和,且每次活动中甲、乙猜对与否互不影响,各次活动也互不影响,则一次活动中,甲获胜的概率为 ;3次活动中,甲至少获胜2次的概率为 .
【答案】;.
【解析】一次活动中,甲获胜的概率为,
次活动中,甲至少获胜2次的概率为.
故答案为:;.
28.(2021•浙江)袋中有4个红球,个黄球,个绿球.现从中任取两个球,记取出的红球数为,若取出的两个球都是红球的概率为,一红一黄的概率为,则 , .
【答案】1;.
【解析】由题意,,
又一红一黄的概率为,
所以,
解得,,故;
由题意,的可能取值为0,1,2,
所以,
,
,
所以.
故答案为:1;.
相关试卷
这是一份【讲通练透】专题14 概率与统计(选择题、填空题)(理)-2021-2023年高考真题分享汇编(全国通用),文件包含专题14概率与统计选择题填空题理全国通用原卷版docx、专题14概率与统计选择题填空题理全国通用解析版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。
这是一份专题07 平面解析几何(选择题、填空题)(学生版)2021-2023年高考数学真题分类汇编(全国通用),共9页。试卷主要包含了若直线是圆的一条对称轴,则,双曲线的左、右焦点分别为,等内容,欢迎下载使用。
这是一份专题05 立体几何(选择题、填空题)(理)(学生版)2021-2023年高考数学真题分类汇编(全国通用),共8页。试卷主要包含了某几何体的三视图如图所示(单位等内容,欢迎下载使用。












