2021-2023年高考数学真题分类汇编(全国通用)专题16算法初步、数系的扩充与复数的引入(学生版+解析)

这是一份2021-2023年高考数学真题分类汇编(全国通用)专题16算法初步、数系的扩充与复数的引入(学生版+解析)，共14页。试卷主要包含了执行下边的程序框图，则输出的，执行下面的程序框图，输出的，执行如图的程序框图，输出的，设，则，已知，则，若，则，若复数满足，则等内容，欢迎下载使用。

知识点1：程序框图
知识点2：复数加减乘除运算
知识点3：模运算
知识点4：复数相等
知识点5：复数的几何意义
近三年高考真题
知识点1：程序框图
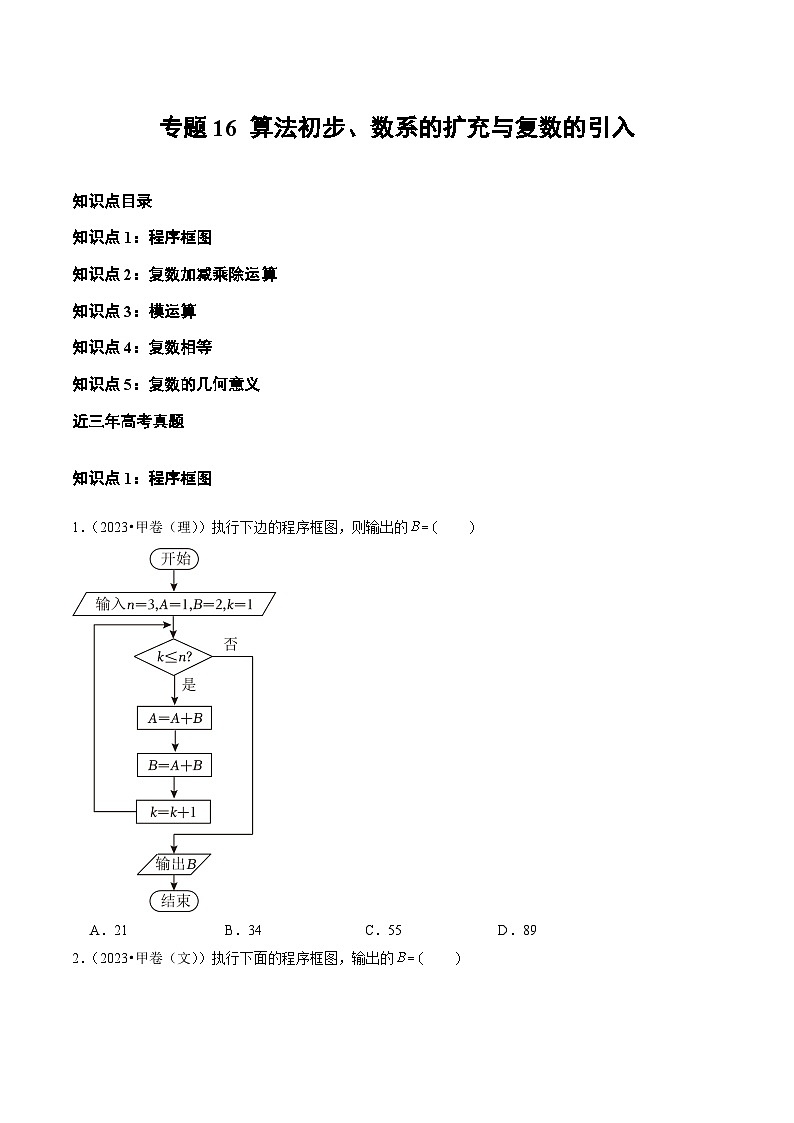
1．（2023•甲卷（理））执行下边的程序框图，则输出的
A．21B．34C．55D．89
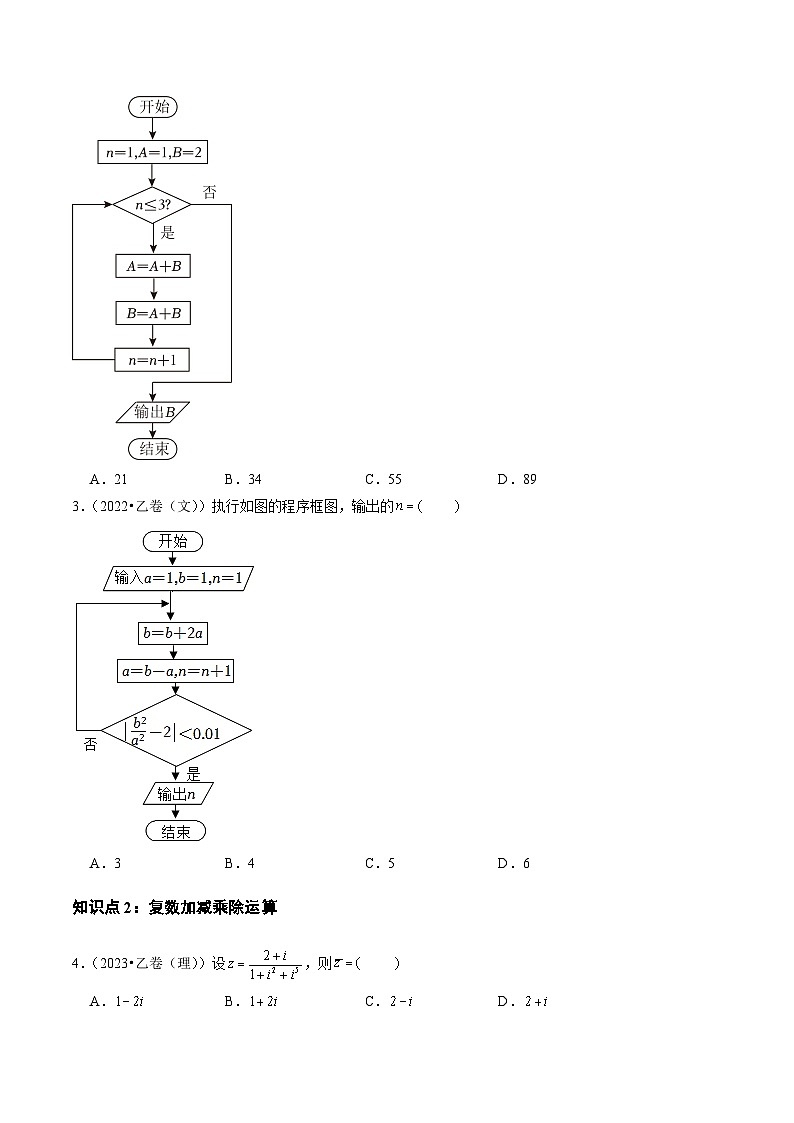
2．（2023•甲卷（文））执行下面的程序框图，输出的
A．21B．34C．55D．89
3．（2022•乙卷（文））执行如图的程序框图，输出的
A．3B．4C．5D．6
知识点2：复数加减乘除运算
4．（2023•乙卷（理））设，则
A．B．C．D．
5．（2023•新高考Ⅰ）已知，则
A．B．C．0D．1
6．（2022•甲卷（理））若，则
A．B．C．D．
7．（2022•新高考Ⅱ）
A．B．C．D．
8．（2022•新高考Ⅰ）若，则
A．B．C．1D．2
9．（2021•北京）若复数满足，则
A．B．C．D．
10．（2021•新高考Ⅰ）已知，则
A．B．C．D．
11．（2023•天津）已知是虚数单位，化简的结果为 ．
12．（2022•天津）已知是虚数单位，化简的结果为 ．
13．（2022•上海）已知（其中为虚数单位），则 ．
14．（2021•天津）是虚数单位，复数 ．
15．（2021•上海）已知，，求 ．
16．（2023•甲卷（文））
A．B．1C．D．
17．（2021•甲卷（文））已知，则
A．B．C．D．
18．（2021•乙卷（文））设，则
A．B．C．D．
知识点3：模运算
19．（2022•北京）若复数满足，则
A．1B．5C．7D．25
20．（2023•乙卷（文））
A．1B．2C．D．5
21．（2022•甲卷（文））若，则
A．B．C．D．
知识点4：复数相等
22．（2022•乙卷（文））设，其中，为实数，则
A．，B．，C．，D．，
23．（2021•浙江）已知，为虚数单位），则
A．B．1C．D．3
24．（2021•乙卷（理））设，则
A．B．C．D．
25．（2023•甲卷（理））若复数，，则
A．B．0C．1D．2
26．（2022•浙江）已知，，为虚数单位），则
A．，B．，C．，D．，
27．（2022•乙卷（理））已知，且，其中，为实数，则
A．，B．，C．，D．，
知识点5：复数的几何意义
28．（2023•北京）在复平面内，复数对应的点的坐标是，则的共轭复数
A．B．C．D．
29．（2023•新高考Ⅱ）在复平面内，对应的点位于
A．第一象限B．第二象限C．第三象限D．第四象限
30．（2021•新高考Ⅱ）复数在复平面内对应点所在的象限为
A．第一象限B．第二象限C．第三象限D．第四象限
专题16 算法初步、数系的扩充与复数的引入
知识点目录
知识点1：程序框图
知识点2：复数加减乘除运算
知识点3：模运算
知识点4：复数相等
知识点5：复数的几何意义
近三年高考真题
知识点1：程序框图
1．（2023•甲卷（理））执行下边的程序框图，则输出的
A．21B．34C．55D．89
【答案】
【解析】模拟执行程序框图，如下：
，，，，
，，，，
，，，，
，，，，
，输出．
故选：．
2．（2023•甲卷（文））执行下面的程序框图，输出的
A．21B．34C．55D．89
【答案】
【解析】根据程序框图列表如下：
故输出的．
故选：．
3．（2022•乙卷（文））执行如图的程序框图，输出的
A．3B．4C．5D．6
【答案】
【解析】模拟执行程序的运行过程，如下：
输入，，，
计算，，，
判断，
计算，，，
判断；
计算，，，
判断；
输出．
故选：．
知识点2：复数加减乘除运算
4．（2023•乙卷（理））设，则
A．B．C．D．
【答案】
【解析】，，
，
．
故选：．
5．（2023•新高考Ⅰ）已知，则
A．B．C．0D．1
【答案】
【解析】，
则，
故．
故选：．
6．（2022•甲卷（理））若，则
A．B．C．D．
【答案】
【解析】，，
则．
故选：．
7．（2022•新高考Ⅱ）
A．B．C．D．
【答案】
【解析】．
故选：．
8．（2022•新高考Ⅰ）若，则
A．B．C．1D．2
【答案】
【解析】由，得，
，则，
．
故选：．
9．（2021•北京）若复数满足，则
A．B．C．D．
【答案】
【解析】因为，
所以．
故选：．
10．（2021•新高考Ⅰ）已知，则
A．B．C．D．
【答案】
【解析】，
．
故选：．
11．（2023•天津）已知是虚数单位，化简的结果为 ．
【答案】．
【解析】．
故答案为：．
12．（2022•天津）已知是虚数单位，化简的结果为 ．
【答案】．
【解析】，
故答案为：．
13．（2022•上海）已知（其中为虚数单位），则 ．
【答案】．
【解析】，则，所以．
故答案为：．
14．（2021•天津）是虚数单位，复数 ．
【答案】．
【解析】复数，
故答案为：．
15．（2021•上海）已知，，求 ．
【答案】
【解析】因为，，
所以．
故答案为：．
16．（2023•甲卷（文））
A．B．1C．D．
【答案】
【解析】．
故选：．
17．（2021•甲卷（文））已知，则
A．B．C．D．
【答案】
【解析】因为，
所以．
故选：．
18．（2021•乙卷（文））设，则
A．B．C．D．
【答案】
【解析】由，得．
故选：．
知识点3：模运算
19．（2022•北京）若复数满足，则
A．1B．5C．7D．25
【答案】
【解析】由，得，
．
故选：．
20．（2023•乙卷（文））
A．1B．2C．D．5
【答案】
【解析】由于．
故选：．
21．（2022•甲卷（文））若，则
A．B．C．D．
【答案】
【解析】，
，
则．
故选：．
知识点4：复数相等
22．（2022•乙卷（文））设，其中，为实数，则
A．，B．，C．，D．，
【答案】
【解析】，
，即，
解得．
故选：．
23．（2021•浙江）已知，为虚数单位），则
A．B．1C．D．3
【答案】
【解析】因为，即，
由复数相等的定义可得，，即．
故选：．
24．（2021•乙卷（理））设，则
A．B．C．D．
【答案】
【解析】设，，是实数，
则，
则由，
得，
得，
得，得，，
即，
故选：．
25．（2023•甲卷（理））若复数，，则
A．B．0C．1D．2
【答案】
【解析】因为复数，
所以，
即，解得．
故选：．
26．（2022•浙江）已知，，为虚数单位），则
A．，B．，C．，D．，
【答案】
【解析】，，，
，，
故选：．
27．（2022•乙卷（理））已知，且，其中，为实数，则
A．，B．，C．，D．，
【答案】
【解析】因为，且，
所以，
所以，
解得，．
故选：．
知识点5：复数的几何意义
28．（2023•北京）在复平面内，复数对应的点的坐标是，则的共轭复数
A．B．C．D．
【答案】
【解析】在复平面内，复数对应的点的坐标是，
，
则的共轭复数，
故选：．
29．（2023•新高考Ⅱ）在复平面内，对应的点位于
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】
【解析】，
则在复平面内，对应的点的坐标为，位于第一象限．
故选：．
30．（2021•新高考Ⅱ）复数在复平面内对应点所在的象限为
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】
【解析】，
在复平面内，复数对应的点的坐标为，，位于第一象限．
故选：．1
3
8
21
2
5
13
34
1
2
3
4