2022年广东省深圳市坪山区中考数学一模试卷

这是一份2022年广东省深圳市坪山区中考数学一模试卷，共30页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）如图，该几何体的左视图是
A．B．C．D．
2．（3分）一元二次方程的根的情况是
A．有两个不相等的实数根B．有两个相等的实数根
C．没有实数根D．无法判断
3．（3分）若与都是反比例函数图象上的点，则的值是
A．4B．C．2D．
4．（3分）解一元二次方程，配方后正确的是
A．B．C．D．
5．（3分）在平面直角坐标系中，将抛物线向上平移2个单位长度，再向右平移1个单位长度，得到的抛物线的解析式是
A．B．C．D．
6．（3分）如图，小明探究课本“综合与实践”板块“制作视力表”的相关内容：当测试距离为时，标准视力表中最大的“”字高度为，当测试距离为时，最大的“”字高度为
A．B．C．D．
7．（3分）如图，的顶点、、均在上，若，则的大小是
A．B．C．D．
8．（3分）下列命题：
①有一个角等于的两个等腰三角形相似；
②对角线互相垂直的四边形是菱形；
③一个角为且一组邻边相等的四边形是正方形；
④对角线相等的平行四边形是矩形．
其中真命题的个数是
A．1B．2C．3D．4
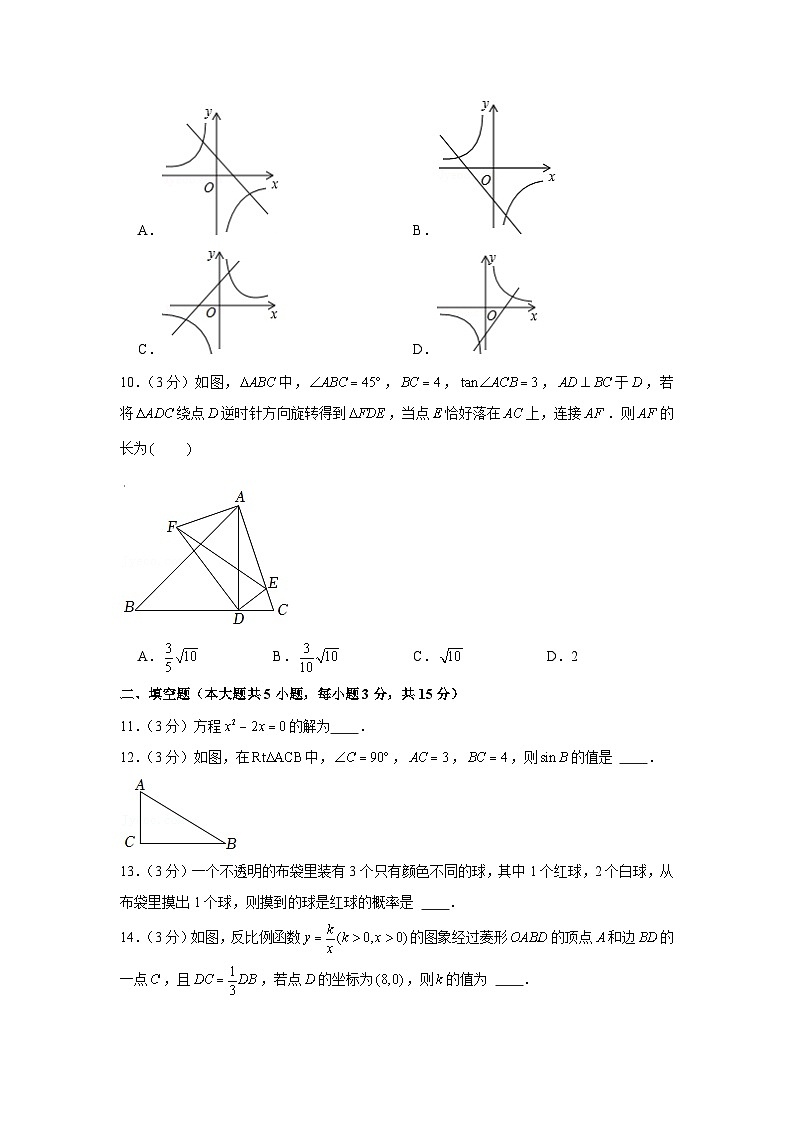
9．（3分）二次函数的图象如图所示，则反比例函数与一次函数在同一坐标系内的大致图象是
A．B．
C．D．
10．（3分）如图，中，，，，于，若将绕点逆时针方向旋转得到，当点恰好落在上，连接．则的长为
A．B．C．D．2
二、填空题（本大题共5小题，每小题3分，共15分）
11．（3分）方程的解为 ．
12．（3分）如图，在中，，，，则的值是 ．
13．（3分）一个不透明的布袋里装有3个只有颜色不同的球，其中1个红球，2个白球，从布袋里摸出1个球，则摸到的球是红球的概率是 ．
14．（3分）如图，反比例函数的图象经过菱形的顶点和边的一点，且，若点的坐标为，则的值为 ．
15．（3分）如图，在正方形中，，为对角线上任意一点（不与、重合），连接，过点作，交线段于点．连接交于点．若，则的值为 ．
三、解答题（本题共7小题，其中第16题5分，第17题7分，第18题8分，第19题8分，第20题8分，第21题9分，第22题10分，共55分）
16．（5分）计算：．
17．（7分）九年级某数学兴趣小组在学习了反比例函数的图象与性质后，进一步研究了函数的图象与性质，其探究过程如下：
（1）绘制函数图象，
列表：下表是与的几组对应值，其中 ．
描点：根据表中各组对应值，在平面直角坐标系中描出各点，请你描出剩下的点；
连线：用平滑的曲线顺次连接各点，已经画出了部分图象，请你把图象补充完整；
（2）通过观察图象，下列关于该函数的性质表述正确的是： ；（填写代号）
①函数值随的增大而增大；②关于轴对称；③关于原点对称；
（3）在上图中，若直线交函数的图象于，两点在左边），连接．过点作交轴于．则 ．
18．（8分）如图为某学校门口“测温箱”截面示意图，当身高1.7米的小聪在地面处时开始显示额头温度，此时在额头处测得的仰角为，当他在地面处时，此时在额头处测得的仰角为，如果测温箱顶部处距地面的高度为3.3米，求、两点的距离．（结果保留一位小数，，，
19．（8分）如图，在中，，点是边上一点，以为直径的与交于点，连接并延长交的延长线于点，且．
（1）求证：为的切线；
（2）若，，求的半径．
20．（8分）某网络经销商购进了一批以冬奥会为主题的文化衫进行销售，文化衫的进价为每件40元，每月销售量（件与销售单价（元之间的函数关系如图所示．
（1）求出每月的销售量（件与销售单价（元之间的函数关系式；
（2）设每月获得的利润为（元．这种文化衫销售单价定为多少元时，每月的销售利润最大？最大利润是多少元？
21．（9分）已知四边形中，、分别是、边上的点，与交于点．
问题发现：
（1）①如图1，若四边形是正方形，且于，则 ；
②如图2，当四边形是矩形时，且于，，，则 ；
拓展研究：
（2）如图3，若四边形是平行四边形，且时，求证：；
解决问题：
（3）如图4，若，，，于，请直接写出的值．
22．（10分）如图，在平面直角坐标系中，抛物线与轴交于、两点在的左侧），与轴交于点，其中，．
（1）求该抛物线的解析式；
（2）如图1，点，是线段上的两点在的右侧），，过点作轴，交直线上方抛物线于点，过点作轴于点，连接，，当面积最大时，求点的坐标及面积的最大值；
（3）如图2，在（2）取得面积最大的条件下，连接，将线段沿射线方向平移，平移后的线段记为，为轴上的动点，是否存在以为直角边的等腰△？若存在，请直接写出点的坐标，若不存在，请说明理由．
2022年广东省深圳市坪山区中考数学一模试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题3分，共30分，每小题有四个选项，其中只有一个是正确的）
1．（3分）如图，该几何体的左视图是
A．B．C．D．
【解答】解：从左边看是一个正方形被水平的分成3部分，中间的两条分线是虚线，故正确；
故选：．
2．（3分）一元二次方程的根的情况是
A．有两个不相等的实数根B．有两个相等的实数根
C．没有实数根D．无法判断
【解答】解：△，
方程有两个不相等的实数根．
故选：．
3．（3分）若与都是反比例函数图象上的点，则的值是
A．4B．C．2D．
【解答】解：与都是反比例函数图象上的点，
，
，
故选：．
4．（3分）解一元二次方程，配方后正确的是
A．B．C．D．
【解答】解：，
，即，
故选：．
5．（3分）在平面直角坐标系中，将抛物线向上平移2个单位长度，再向右平移1个单位长度，得到的抛物线的解析式是
A．B．C．D．
【解答】解：将抛物线向上平移2个单位长度，再向右平移1个单位长度，得到的抛物线的解析式是．
故选：．
6．（3分）如图，小明探究课本“综合与实践”板块“制作视力表”的相关内容：当测试距离为时，标准视力表中最大的“”字高度为，当测试距离为时，最大的“”字高度为
A．B．C．D．
【解答】解：由题意得：，
，
，，，
，
，
故选：．
7．（3分）如图，的顶点、、均在上，若，则的大小是
A．B．C．D．
【解答】解：，
而，
，
．
故选：．
8．（3分）下列命题：
①有一个角等于的两个等腰三角形相似；
②对角线互相垂直的四边形是菱形；
③一个角为且一组邻边相等的四边形是正方形；
④对角线相等的平行四边形是矩形．
其中真命题的个数是
A．1B．2C．3D．4
【解答】解：①有一个角等于的两个等腰三角形相似，是真命题；
②对角线互相垂直的平行四边形是菱形，故原说法是假命题；
③一个角为且邻边相等的四边形是正方形，故原说法是假命题；
④对角线相等的平行四边形是矩形，是真命题，
故真命题有①④，共2个，
故选：．
9．（3分）二次函数的图象如图所示，则反比例函数与一次函数在同一坐标系内的大致图象是
A．B．
C．D．
【解答】解：二次函数的图象开口向上，
，
二次函数的图象的对称轴在轴的左侧，且交轴的负半轴，
，，
反比例函数的图象必在一、三象限，一次函数的图象必经过一三四象限，故正确．
故选：．
10．（3分）如图，中，，，，于，若将绕点逆时针方向旋转得到，当点恰好落在上，连接．则的长为
A．B．C．D．2
【解答】解：过点作于点，
，，
，
，
设，
，
，
，
，，
，
将绕点逆时针方向旋转得到，
，，，
，
，
设，，
，
，
，
，
．
故选：．
二、填空题（本大题共5小题，每小题3分，共15分）
11．（3分）方程的解为 ， ．
【解答】解：，
，
或，
或．
故答案为：，．
12．（3分）如图，在中，，，，则的值是 ．
【解答】解：，，，
，
，
故答案为：．
13．（3分）一个不透明的布袋里装有3个只有颜色不同的球，其中1个红球，2个白球，从布袋里摸出1个球，则摸到的球是红球的概率是 ．
【解答】解：布袋装有3个只有颜色不同的球，1个红球，
从布袋里摸出1个球，摸到红球的概率．
故答案为：．
14．（3分）如图，反比例函数的图象经过菱形的顶点和边的一点，且，若点的坐标为，则的值为 ．
【解答】解：作轴于，轴于，
四边形是菱形，点的坐标为，
，，
，
，
，
，
，
，
，，
设，，则，，
点、在反比例函数的图象上，
，
，
，
，，
在中，，
，解得，
，
，
故答案为：．
15．（3分）如图，在正方形中，，为对角线上任意一点（不与、重合），连接，过点作，交线段于点．连接交于点．若，则的值为 15 ．
【解答】解：如图，把绕点逆时针旋转得到，连接，
，，
，，，，
，，
，
、、、四点共圆，
，
，
，
，
，
设，则，
在中，，则，
正方形的边长为，
，
，
，
，，
，，
，
，
．
故答案为：15．
三、解答题（本题共7小题，其中第16题5分，第17题7分，第18题8分，第19题8分，第20题8分，第21题9分，第22题10分，共55分）
16．（5分）计算：．
【解答】解：
．
17．（7分）九年级某数学兴趣小组在学习了反比例函数的图象与性质后，进一步研究了函数的图象与性质，其探究过程如下：
（1）绘制函数图象，
列表：下表是与的几组对应值，其中 ．
描点：根据表中各组对应值，在平面直角坐标系中描出各点，请你描出剩下的点；
连线：用平滑的曲线顺次连接各点，已经画出了部分图象，请你把图象补充完整；
（2）通过观察图象，下列关于该函数的性质表述正确的是： ；（填写代号）
①函数值随的增大而增大；②关于轴对称；③关于原点对称；
（3）在上图中，若直线交函数的图象于，两点在左边），连接．过点作交轴于．则 ．
【解答】解：（1）将代入得，
故答案为：．
（2）由（1）中的图象可知，在第一象限内，随的增大而减小；在第二象限内，随的增大而增大；函数图象关于轴对称，
故②正确；
故答案为：②．
（3）将代入得或，
，
在直线上，在轴上，
，
又，
四边形为平行四边形，
．
故答案为：4．
18．（8分）如图为某学校门口“测温箱”截面示意图，当身高1.7米的小聪在地面处时开始显示额头温度，此时在额头处测得的仰角为，当他在地面处时，此时在额头处测得的仰角为，如果测温箱顶部处距地面的高度为3.3米，求、两点的距离．（结果保留一位小数，，，
【解答】解：如图，延长交于点，
米，且，，
，
四边形是平行四边形，
，
平行四边形是矩形，
同理，四边形是矩形，
米，
（米，
在中，，，
，
（米，
在中，，，
，
（米，
（米，
答：、两点的距离约为0.6米．
19．（8分）如图，在中，，点是边上一点，以为直径的与交于点，连接并延长交的延长线于点，且．
（1）求证：为的切线；
（2）若，，求的半径．
【解答】（1）证明：如图，连接，
，
，
，
，
，
，
，
，
，
为半径，
为的切线；
（2）解：如图，连接，
，
，
，
，
，
是直径，
，
，
又，，
，
，
，
，
的半径．
20．（8分）某网络经销商购进了一批以冬奥会为主题的文化衫进行销售，文化衫的进价为每件40元，每月销售量（件与销售单价（元之间的函数关系如图所示．
（1）求出每月的销售量（件与销售单价（元之间的函数关系式；
（2）设每月获得的利润为（元．这种文化衫销售单价定为多少元时，每月的销售利润最大？最大利润是多少元？
【解答】解：（1）设与之间的函数关系式为：，
将，代入得：，
解得：，
与之间的函数关系式为；
（2）由题意得：，
配方得：，
，
当时，有最大值为9000，
答：这种文化衫销售单价定为70元时，每月的销售利润最大，最大利润是9000元．
21．（9分）已知四边形中，、分别是、边上的点，与交于点．
问题发现：
（1）①如图1，若四边形是正方形，且于，则 1 ；
②如图2，当四边形是矩形时，且于，，，则 ；
拓展研究：
（2）如图3，若四边形是平行四边形，且时，求证：；
解决问题：
（3）如图4，若，，，于，请直接写出的值．
【解答】（1）解：①四边形是正方形，
，，
，
，
，
，
，
，
，
故答案为：1；
②解：四边形是矩形，
，，
，
，
，，
，
，
，
，
故答案为：；
（2）证明：如图所示，，，
，
在的延长线上取点，使，则，
，
，
，
，
，
，
，
，
，
即；
（3）解：过作于，交延长线于，连接，设，
，即，
，
四边形是矩形，
，，
在和中，
，
，
，
，
，
，
，
，
，
，
，
在中，，，由勾股定理得：，
，
解得：（舍去），，
，
，
，
，
，
，
，
．
22．（10分）如图，在平面直角坐标系中，抛物线与轴交于、两点在的左侧），与轴交于点，其中，．
（1）求该抛物线的解析式；
（2）如图1，点，是线段上的两点在的右侧），，过点作轴，交直线上方抛物线于点，过点作轴于点，连接，，当面积最大时，求点的坐标及面积的最大值；
（3）如图2，在（2）取得面积最大的条件下，连接，将线段沿射线方向平移，平移后的线段记为，为轴上的动点，是否存在以为直角边的等腰△？若存在，请直接写出点的坐标，若不存在，请说明理由．
【解答】解：（1）将，代入，得
，解得：，
抛物线的解析式为：．
（2）过点作于点，
令，得，
解得：，，
，
，，
，
，，
，
，
，即，
，
解得：，
设直线的解析式为：，则
，解得：，
直线的解析式为：，
设，，则，
，
配方得：，
，
时，有最大值为，
点的坐标为时，的面积最大值为．
（3）设，，，
，，线段沿射线方向平移，
，
①如图2，当点在轴右侧，时，，
过点作轴于点，过点作于点，则，，
，
，
△△，
，，
，，，，
，且，舍去；
②如图3，当点在轴右侧，时，，
过点作轴于点，过点作的延长线于点，则，，
，
，
△△，
，，
，，，，
，且，
，，舍去；
③如图4，当点在轴左侧，时，，
过点作轴于点，过点作于点，则，，
，
，
△△，
，，
，，，，
，且，
，，
点的坐标为；
④如图5，当点在轴左侧，时，，
过点作轴于点，过点作的延长线于点，则，，
，
，
△△，
，，
，，，，
，且，
，，
点的坐标为；
综上所述，△是以为直角边的等腰直角三角形时，点的坐标为或．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/3/9 17:12:26；用户：刘聪；邮箱：18576686425；学号：240751331
2
3
1
2
4
4
2
1
1
2
3
1
2
4
4
2
1