人教版八年级下册18.1.1 平行四边形的性质课文ppt课件

这是一份人教版八年级下册18.1.1 平行四边形的性质课文ppt课件，共20页。PPT课件主要包含了探索一，探索三，巩固练习，变式题，课堂小结等内容，欢迎下载使用。
两组对边分别平行的四边形叫做平行四边形。
1、平行四边形的定义：
4.两条平行直线之间的距离相等
3.夹在两条平行线间的平行线段相等.
数学来源于生活，高铁被外媒誉为我国新四大发明之一，我们知道铁路的两条直铺的铁轨互相平行，那么铁路工人是怎样的确保它们平行的呢？
只要使互相平行的夹在铁轨之间的枕木长相等就可以了
那这是为什么呢？会不会跟我们学过的平行四边形有关呢？
我们知道了平行四边形的性质，那么，有哪些方法可以判断一个四边形是平行四边形呢？
根据定义是一种最基本、最重要的判定方法。
判定1.两组对边平行的四边形是平行四边形.
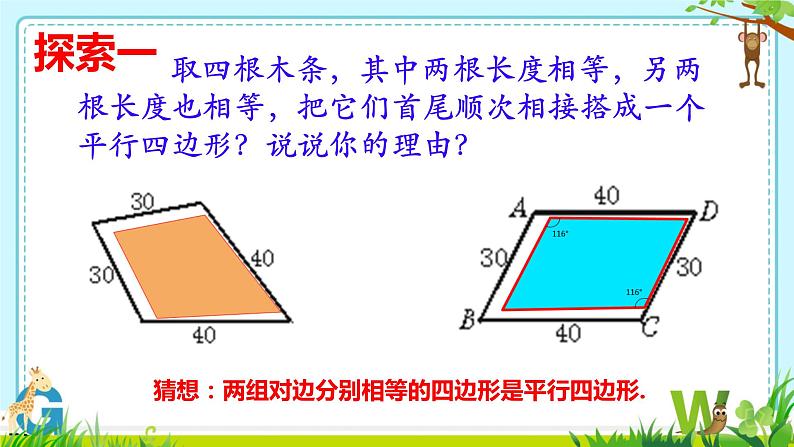
取四根木条，其中两根长度相等，另两根长度也相等，把它们首尾顺次相接搭成一个平行四边形？说说你的理由？
猜想：两组对边分别相等的四边形是平行四边形.
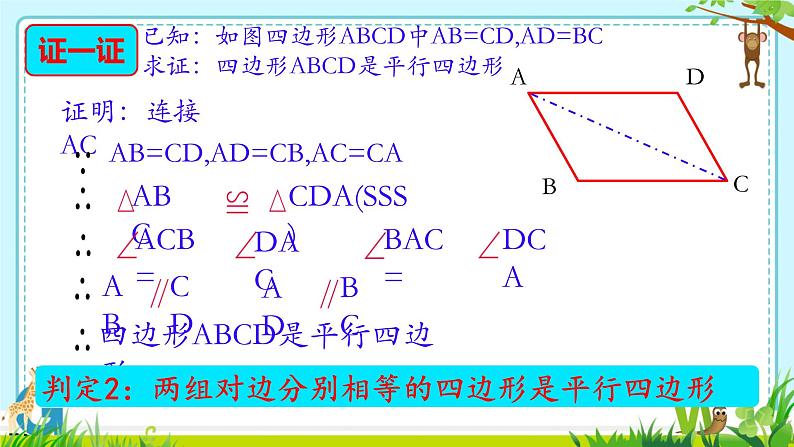
已知：如图四边形ABCD中AB=CD,AD=BC求证：四边形ABCD是平行四边形
AB=CD,AD=CB,AC=CA
四边形ABCD是平行四边形
判定2：两组对边分别相等的四边形是平行四边形
按照下面的步骤，在方格纸上画一个四边形。1、画一线段AD.2、平移线段AD到BC.3、连结AB、DC，得到四边形ABCD。
四边形ABCD是哪一种特殊的四边形？由此，你能得到什么结论？
一组对边平行且相等的四边形是平行四边形。
已知：在四边形ABCD中， AD 　BC。
求证：四边形ABCD是平行四边形。
∵AD=CB，AC=CA，
∴ΔADC ≌ ΔCBA（)
∴四边形ABCD是平行四边形
判定3：一组对边平行且相等的四边形是平行四边形.
如图,将两根细木条AC、BD的中点重叠，用小钉固定在一起，用橡皮筋连接木条的顶点，做成一个四边形ABCD.转动两根木条，四边形ABCD一直是一个平行四边形吗？
猜想：对角线互相平分的四边形是平行四边形.
你能根据平行四边形的定义证明它们吗？
如图，在四边形ABCD中,AC,BD相交于点O,且OA=OC,OB=OD.求证：四边形ABCD是平行四边形．
证明：∵OA=OC,OB=OD,∠AOD=∠COB, ∴△AOD≌△COB． ∴∠OAD=∠OCB． ∴AD∥BC． 同理AB∥DC． ∴四边形ABCD是平行四边形．
判定4：对角线互相平分的四边形是平行四边形.
学习了平行四边形后，小明回家用细木棒钉制了一个平行四边形．第二天，小明拿着自己动手做的平行四边形向同学们展示． 小亮却问：你凭什么确定这四边形就是平行四边形呢？ 大家都困惑了……
猜想：两组对角分别相等的四边形是平行四边形.
证明：∵多边形ABCD是四边形， ∴∠A+∠B+∠C+∠D=360°． 又∵∠A=∠C，∠B=∠D， ∴∠A+∠B=180°，∠B+∠C=180°． ∴AD∥BC，AB∥DC．∴四边形ABCD是平行四边形
如图，在四边形ABCD中，∠A=∠C，∠B=∠D．求证：四边形ABCD是平行四边形．
判定5：两组对角分别相等的四边形是平行四边形.
总结：平行四边形判定定理
判定1：两组对边分别平行的四边形是平行四边形 （定义判定法）
判定2：两组对边分别相等的四边形是平行四边形.
例1.已知：E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF ．求证：四边形BFDE是平行四边形．
证明：作对角线BD，交AC于点O
∵四边形ABCD是平行四边形
∴ AO=CO，BO=DO
∴AO-AE=CO-CF
∴ 四边形BFDE是平行四边形
（对角线互相平分的四边形是平行四边形）
例2 如图6-10，在平行四边ABCD中，E、F分别是AD和BC的中点．求证：四边形BFDE是平行四边形.
证明： ∵ 四边形ABCD是平行四边形 ∴ AD=CB AD//BC又∵E、F分别是AD和BC的 中点 ∴ ED= AD BF= BC ∴ DE=BF又∵DE∥BF ∴ 四边形BFDE是平行四边形
（一组对边平行且相等的四边形是平行四边形）
例3.如图，点C是AB的中点，AD=CE，CD=BE．（1）求证：△ACD≌△CBE；（2）求证：四边形CBED是平行四边形．
证明：（1）∵点C是AB的中点，∴AC=BC.在△ADC与△CEB中， AD＝CE , CD＝BE , AC＝CB ,∴△ADC≌△CEB（SSS），（2）∵△ADC≌△CEB，∴∠ACD=∠CBE，∴CD∥BE.又∵CD=BE，∴四边形CBED是平行四边形．