高教版（2021·十四五）基础模块 下册5.2 指数函数精品课后复习题

这是一份高教版（2021·十四五）基础模块 下册5.2 指数函数精品课后复习题，文件包含专题02指数函数原卷版docx、专题02指数函数解析版docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
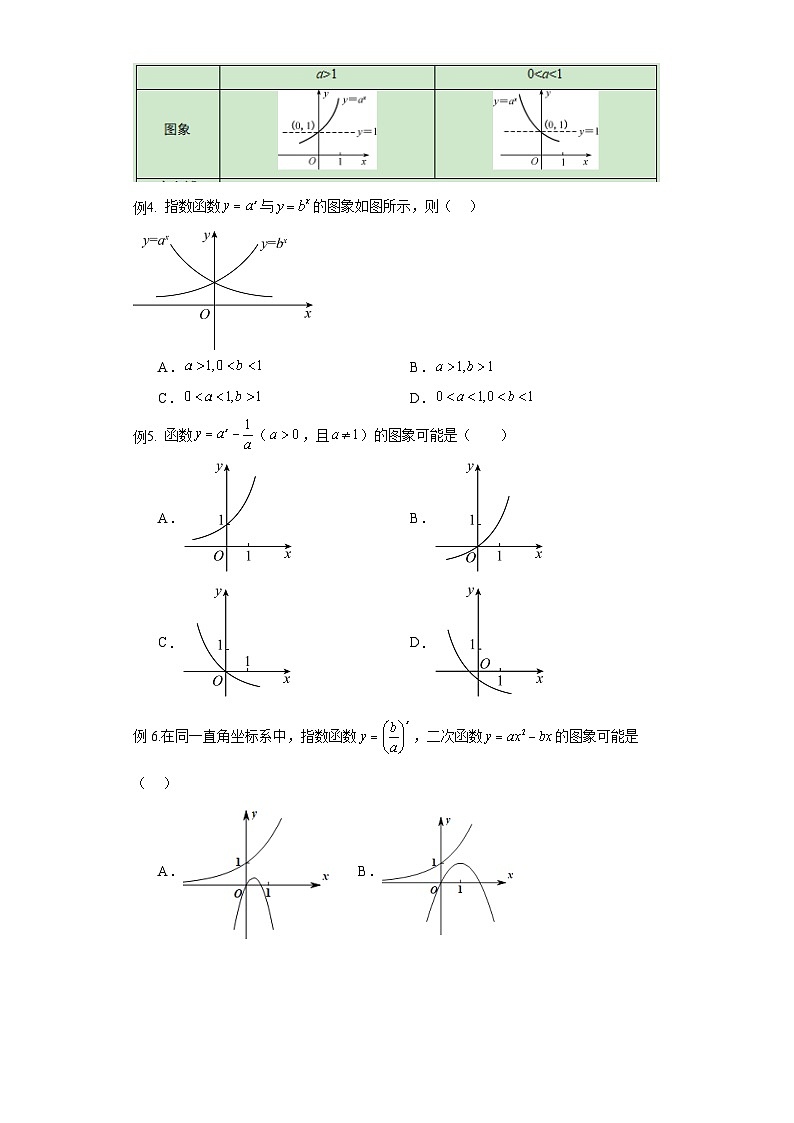
函数y＝ax(a>0且a≠1)叫做指数函数，其中指数x是自变量，函数的定义域是R，a是底数．
指数函数的图象与性质
注意：
1.指数函数的特征：
(1)底数a为大于0且不等于1的常数；
(2)指数位置是自变量x；
(3)ax的系数是1.
2. 函数图像对称性：
函数y＝ax与y＝(a>0且a≠1)的图象关于y轴对称．
【题型1 指数函数的判断及求解析式】
【题型2 指数函数的图像】
【题型3 指数函数的图像与性质综合】
【题型4 指数函数的应用】
【题型1 指数函数的判断及求解析式】
知识点：（1）指数函数的概念：函数y＝ax(a>0且a≠1)叫做指数函数，其中指数x是自变量，函数的定义域是R，a是底数．
（2）指数函数的三个特征：底数a为大于0且不等于1的常数；指数位置是自变量x；ax的系数是1.
例1.下列函数：①；②；③；④．其中为指数函数的个数是（ ）
A．B．
C．D．
例2．若函数是指数函数，则（ ）
A．或B．
C．D．且
例3．若指数函数的图象过点，则的解析式为（ ）
A．B．C．D．
【题型训练1】
1．（多选）下列函数是指数函数的是（ ）
A． B． C． D．（且）
2．若函数为指数函数，则（ ）
A．或B．且
C．D．
3．若函数是指数函数，且，则（ ）
A．B．
C．D．
【题型2 指数函数的图像】
知识点：
指数函数与的图象如图所示，则（ ）
A．B．
C．D．
函数（，且）的图象可能是（ ）
A． B．
C． D．
例6.在同一直角坐标系中，指数函数，二次函数的图象可能是（ ）
A． B．
C． D．
【题型训练2】
1．（多选）已知函数，且的图象如图所示，则下列结论正确的是（ ）
A．B．C．D．
2．要得到函数的图象，只需将指数函数的图象（ ）
A．向左平移1个单位B．向右平移1个单位
C．向左平移个单位D．向右平移个单位
【题型3 指数函数的图像与性质综合】
例7. 函数 的定义域是（ ）
A．B．
C．D．
例8．函数的值域是（ ）
A．B．C．D．
例9．设，，，则（ ）
A．B．C．D．
【题型训练3】
1．函数的定义域为（ ）
A．B．C．D．
2．函数，的值域是（ ）
A．B．C．D．
3．若，，，则它们的大小关系是（ ）
A．B．C．D．
4．函数在上的最大值是（ ）
A．B．0
C．1D．3
【题型4 指数函数的应用】
例10．某种细胞分裂时，由1个分裂成2个，2个分裂成4个，……现有2个这样的细胞，分裂x次后得到细胞的个数y与x的函数关系是（ ）
A．y＝2xB．y＝
C．y＝D．y＝
例11．某工厂在某年12月份的产值是这年1月份的产值的m倍，则该厂在本年度的产值的月平均增长率为（ ）
A．B．C．D．
例12．按复利计算利息的一种储蓄，本金为a(单位：元)，每期利率为r，本利和为y(单位：元)，存期数为x.
（1）写出本利和y关于存期数x的函数解析式；
（2）如果存入本金1000元，每期利率为2.25%，试计算5期后的本利和.复利是一种计算利息的方法，即把前一期的利息和本金加在一起算作本金，再计算下一期的利息.我国现行定期储蓄中的自动转存业务就是类似复利计算的储蓄.
【题型训练3】
1．为了给地球减负，提高资源利用率，2019年全国掀起了垃圾分类的热潮，垃圾分类已经成为新时尚，假设某市2019年全年用于垃圾分类的资金为5000万元，在此基础上，每年投入的资金比上一年增长20%，则该市全年用于垃圾分类的资金开始超过1.28亿元的年份是（参考数据：，）
A．2023年B．2024年C．2025年D．2026年
2．当生物死亡后，它机体内原有的碳14含量会按确定的比率衰减(称为衰减率)，大约每经过5730年衰减为原来的一半，这个时间称为“半衰期”.若按照上述变化规律，则死亡生物体内碳14含量每年的衰减率为 .
3．如图，某城市人口呈指数增长.
（1）根据图象，估计该城市人口每翻一番所需的时间（倍增期）；
（2）该城市人口从80万人开始，经过20年会增长到多人少万人？
4．在某个时期，某湖泊中的蓝藻每天以6.25%的增长率呈指数增长，那么经过30天，该湖泊的蓝藻会变为原来的多少倍？（可以使用计算工具）
5．某科研小组培育一种水稻新品种，由第1代1粒种子可以得到第2代120粒种子，以后各代每粒种子都可以得到下一代120粒种子．写出第n代得到的种子数与n的函数关系式，并求第5代得到的种子数．（结果写成（，n为正整数）的形式，a精确到0.01）
a>1
01 ；
当x