基础模块 下册6.5 直线与圆的位置关系优秀同步测试题

这是一份基础模块 下册6.5 直线与圆的位置关系优秀同步测试题，文件包含专题10直线与圆的位置关系原卷版docx、专题10直线与圆的位置关系解析版docx等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。
直线与圆的位置关系
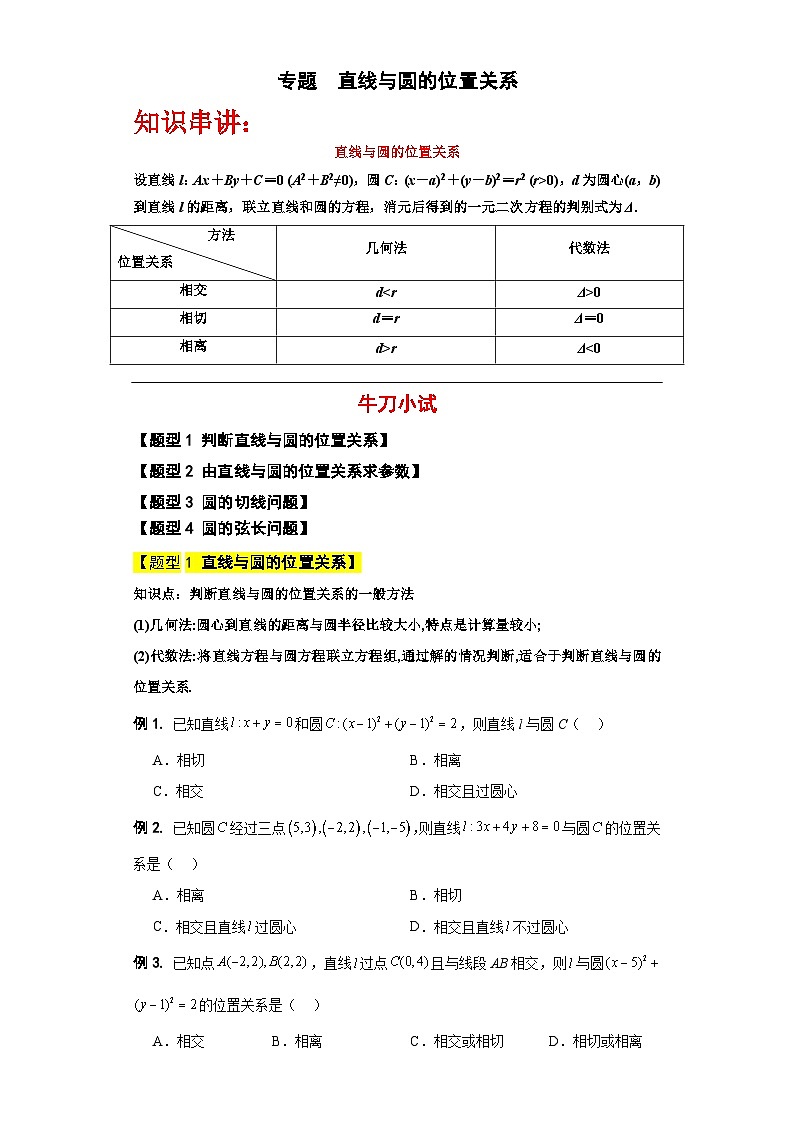
设直线l：Ax＋By＋C＝0 (A2＋B2≠0)，圆C：(x－a)2＋(y－b)2＝r2 (r>0)，d为圆心(a，b)到直线l的距离，联立直线和圆的方程，消元后得到的一元二次方程的判别式为Δ.
【题型1 判断直线与圆的位置关系】
【题型2 由直线与圆的位置关系求参数】
【题型3 圆的切线问题】
【题型4 圆的弦长问题】
【题型1 直线与圆的位置关系】
知识点：判断直线与圆的位置关系的一般方法
(1)几何法:圆心到直线的距离与圆半径比较大小,特点是计算量较小;
(2)代数法:将直线方程与圆方程联立方程组,通过解的情况判断,适合于判断直线与圆的位置关系.
例1. 已知直线和圆，则直线l与圆C（ ）
A．相切B．相离
C．相交D．相交且过圆心
例2. 已知圆经过三点，则直线与圆的位置关系是（ ）
A．相离B．相切
C．相交且直线过圆心D．相交且直线不过圆心
例3. 已知点，直线过点且与线段AB相交，则与圆的位置关系是（ ）
A．相交B．相离C．相交或相切D．相切或相离
例4.已知点在圆内，则直线与圆的位置关系是 .
【题型训练1】
1．直线与圆的位置关系为（ ）
A．相交且过圆心B．相交且不过圆心
C．相切D．相离
2.直线与圆的位置关系为（ ）
A．相离B．相切C．相交D．无法确定
3.已知在圆外，则直线与圆的位置关系是（ ）
A．相交B．相切C．相离D．以上皆有可能
4.直线与圆的公共点个数为（ ）
A．0B．1C．2D．不确定
【题型2由直线与圆的位置关系求参数】
知识点：根据直线与圆的位置关系，可以得到圆心到直线的距离与半径的大小关系，以及直线与圆的公共点个数，从而进行计算求出相关参数.
例5. 若圆与轴相切，则（ ）
A．1B．C．2D．4
例6. 若直线与圆只有一个公共点，则（ ）
A．0B．1C．D．2
例7. 若对任意实数，直线与圆至少有一个交点，则实数的取值范围是 ．
【题型训练2】
1．若直线（）与圆相切，则 .
2．若直线与圆只有一个公共点，则（ ）
A．B．1C．0D．2
3.已知直线与圆相交，则实数的取值范围是（ ）
A．B．C．D．
4.（多选）若直线与圆有公共点，则实数的取值可能是（ ）
A．0B．2C．3D．4
【题型3 圆的切线问题】
知识点： 求过某点的圆的切线的方法
(1)确定点与圆的位置关系,再求切线方程.
(2)若点在圆上(即为切点),则过该点的切线只有一条;若点在圆外,则过该点的切线有两条,此时注意斜率不存在的切线.
例8. 已知圆，过点作圆的切线，则该切线的一般式方程为（ ）
A．B．
C．D．
例9. 直线l过点，且与圆相切，则直线l的方程为（ ）
A．B．
C．D．或
例10. 已知圆经过两点，，且圆心在直线上.
(1)求圆的标准方程；
(2)求过点且与圆相切的直线方程.
例11. 已知点在圆上，直线平分圆.
(1)求圆的标准方程；
(2)求过点且与圆相切的直线方程.
【题型训练3】
1．圆在点处的切线方程为 .
2．过点且与圆相切的直线方程为（ ）
A．B．
C．或D．或
3．过点与圆相切的直线方程为 ．
4．已知的圆心为，且过点．
(1)求的标准方程；
(2)若直线与相切于点，求的方程．
5．已知圆经过点，，.
(1)求圆的方程；
(2)过点作直线与圆相切，求直线的方程.
【题型4 圆的弦长问题】
知识点：弦长的两种求法
(1) 几何法：直线被圆截得的半弦长eq \f(l,2)、弦心距d和圆的半径r构成直角三角形，即r2＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(l,2)))2＋d2.
(2) 代数法：联立直线的方程和圆的方程，消去y转化为关于x的一元二次方程，由根与系数的关系即可求得弦长|AB|＝eq \r(1＋k2)|x2－x1|＝eq \r(1＋k2)·eq \r(x1＋x22－4x1x2)或|AB|＝eq \r(1＋\f(1,k2))|y2－y1|＝eq \r(1＋\f(1,k2))·eq \r(y1＋y22－4y1y2)(k为直线的斜率且k≠0，A(x1，y1)，B(x2，y2)为直线与圆的两个交点)．
例12. 直线被圆截得的弦长为
例13. 过三点，，的圆交轴于，两点，则（ ）
A．B．C．D．
例14. 已知圆：与直线，下列选项正确的是（ ）
A．直线与圆相切B．直线与圆相离
C．直线与圆相交且所截弦长最短为D．直线与圆相交且所截弦长最短为4
例15.圆的圆心为，且过点.
(1)求圆的标准方程；
(2)直线：与圆交，两点，且，求.
【题型训练4】
1．直线被圆截得的弦长为 .
2．过圆外一点作圆的切线，切点分别为，，则（ ）
A．B．C．D．
3．已知两点，以线段为直径的圆截直线所得弦长为（ ）
A．B．C．4D．2
4.已知直线与圆交于A，B两点，且，则实数（ ）
A．4B．3C．2D．1
5.已知圆的圆心在直线上，且圆与轴相切于点．
(1)求圆的标准方程；
(2)若直线与圆相交于两点，求．
方法
位置关系
几何法
代数法
相交
d0
相切
d＝r
Δ＝0
相离
d>r
Δ