高教版（2021）拓展模块二 下册6.5 三角计算的应用优秀学案及答案

这是一份高教版（2021）拓展模块二 下册6.5 三角计算的应用优秀学案及答案，文件包含第6章三角计算知识考点-中职专用高中数学单元复习讲与测高教版2021·拓展模块一下册原卷版docx、第6章三角计算知识考点-中职专用高中数学单元复习讲与测高教版2021·拓展模块一下册解析版docx等2份学案配套教学资源，其中学案共17页， 欢迎下载使用。

知识点一：和角公式
1．两角和与差的余弦公式
2．两角和与差的正弦公式
3．两角和与差的正切公式
知识点二：二倍角公式、降幂公式、辅助角公式
1．
2．
3．
4．，
5．==
（其中和）
知识点三：正弦型函数的图像和性质
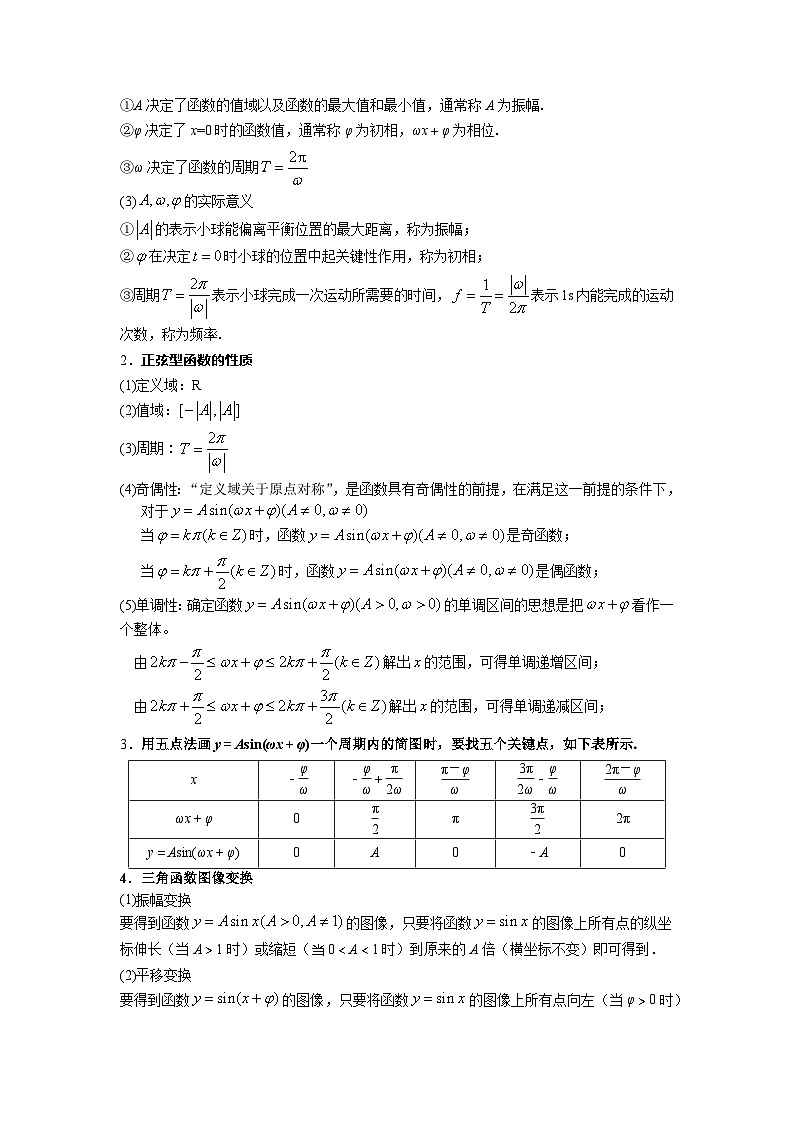
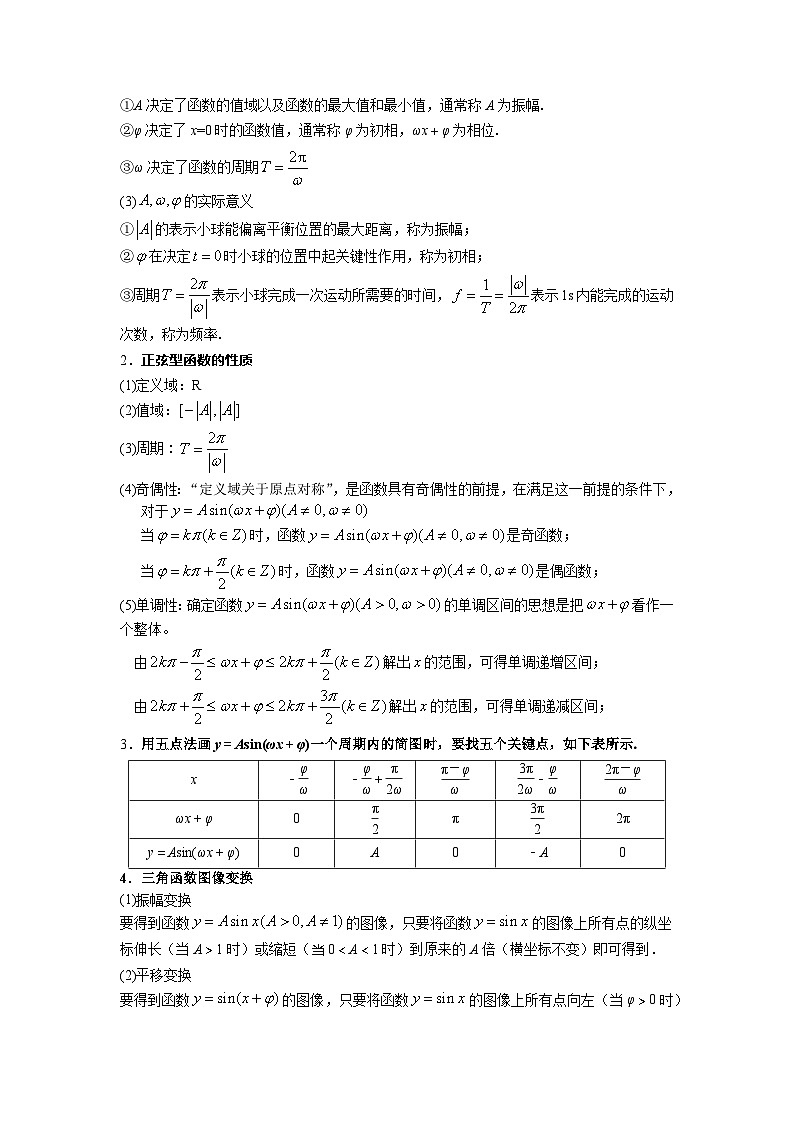
1．正弦型函数的相关概念
(1)定义：一般地，形如的函数，在物理，工程等学科的研究中经常遇到，这类型的函数称为正弦型函数，其中都是常数，且.
(2)对函数图像的影响
①A决定了函数的值域以及函数的最大值和最小值，通常称A为振幅.
②φ决定了x=0时的函数值，通常称φ为初相，ωx＋φ为相位.
③ω决定了函数的周期
(3)的实际意义
①的表示小球能偏离平衡位置的最大距离，称为振幅；
②在决定时小球的位置中起关键性作用，称为初相；
③周期表示小球完成一次运动所需要的时间，表示1s内能完成的运动次数，称为频率.
2．正弦型函数的性质
(1)定义域：R
(2)值域：
(3)周期：
(4)奇偶性：“定义域关于原点对称”，是函数具有奇偶性的前提，在满足这一前提的条件下，
对于
当时，函数是奇函数；
当时，函数是偶函数；
(5)单调性：确定函数的单调区间的思想是把看作一个整体。
由解出的范围，可得单调递增区间；
由解出的范围，可得单调递减区间；
3．用五点法画y＝Asin(ωx＋φ)一个周期内的简图时，要找五个关键点，如下表所示.
4．三角函数图像变换
(1)振幅变换
要得到函数的图像，只要将函数的图像上所有点的纵坐标伸长（当A＞1时）或缩短（当0＜A＜1时）到原来的A倍（横坐标不变）即可得到．
(2)平移变换
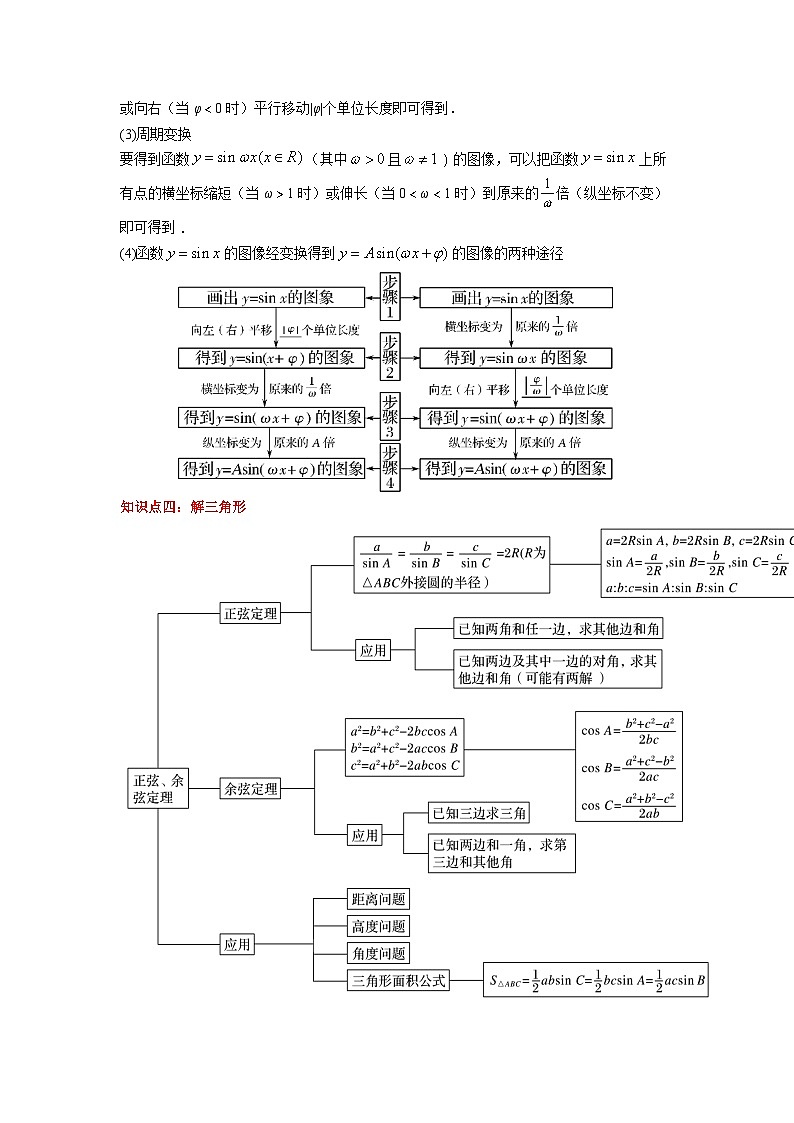
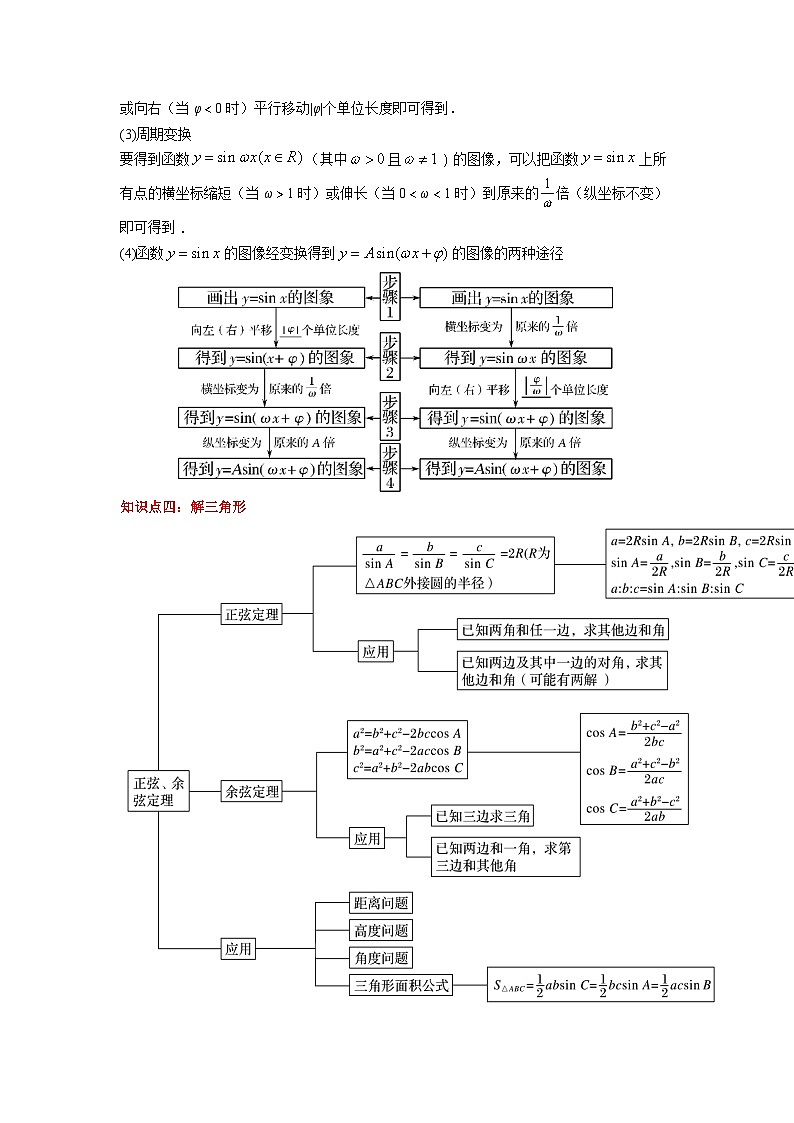
要得到函数的图像，只要将函数的图像上所有点向左（当φ＞0时）或向右（当φ＜0时）平行移动|φ|个单位长度即可得到．
(3)周期变换
要得到函数（其中且）的图像，可以把函数上所有点的横坐标缩短（当ω＞1时）或伸长（当0＜ω＜1时）到原来的倍（纵坐标不变）即可得到．
(4)函数的图像经变换得到的图像的两种途径
知识点四：解三角形
考点一 三角恒等变换（三角和差公式、二倍角公式、降幂公式、辅助角公式）
1．（ ）
A． B． C． D．
【答案】D
【解析】.故选：D.
2．（ ）
A． B． C． D．
【答案】C
【解析】，故选：C.
3．（ ）
A．-1 B． C． D．1
【答案】C
【解析】.故选：C.
4． 已知都为锐角，则的值为 .
【答案】
【解析】因为都是锐角，所以，，，
所以，故答案为：.
5．化简，得其结果为 .
【答案】
【解析】
，故答案为：.
6．已知，则（ ）
A． B． C． D．
【答案】B
【解析】因为，得，所以．故选：B.
7．化简：（ ）
A． B． C． D．
【答案】C
【解析】，故选：C.
8．已知，则（ ）
A． B． C． D．
【答案】A
【解析】由，得，则.故选：A
9．下列计算中不正确的是（ ）
A． B．
C． D．
【答案】B
【解析】对于A，，故A正确；
对于B，，故B错误；
对于C，，故C正确；
对于D，，故D正确.故选：B.
10．已知，则（ ）
A． B． C． D．
【答案】D
【解析】，则，则，故选：D.
11．若，则（ ）
A． B． C． D．
【答案】D
【解析】，分子分母同时除以，得．故选：D.
12．函数的最小正周期为___________.
【答案】
【解析】因为
，即，所以的最小正周期；故答案为：.
13．在单位圆中，角的终边与单位圆的交点为，其中.
（1）求的值；
（2）求的值.
【答案】(1)；(2)
【解析】解：（1）由A在单位圆上，则，又，则，则，，则；
（2），又，则.
考点二 正弦型函数的图像和性质
14．把函数图象上所有点的横坐标伸长到原来的2倍，纵坐标不变，再把所得图象向右平移个单位长度，得到图象对应的解析式为（ ）
A． B．
C． D．
【答案】B
【解析】将函数图象上所有点的横坐标伸长到原来的2倍，纵坐标不变得到，
将向右平移个单位长度得到，故选：B.
15．函数的最小正周期为（ ）
A．π B．2π C．4π D．6π
【答案】A
【解析】由题意最小正周期是，故选：A．
16．函数的图象的一个对称轴方程是（ ）
A． B． C． D．
【答案】C
【解析】对于函数，令，解得，故函数的对称轴方程为，令，可知函数的一条对称轴为.故选：C.
17．函数的单调增区间是（ ）
A． B．
C． D．
【答案】B
【解析】因为，令，，解得，，
所以函数的单调递增区间为；故选：B.
18．函数的部分图象如图所示，则（ ）
A． B．
C． D．
【答案】B
【解析】由图象可得：，∴，再根据五点法作图可得，，，又，∴，∴故选：B.
考点三 解三角形
19．在中，，，，则边AC的长为（ ）
A．B．3C．D．
【答案】C
【解析】由题意，在中，，，，由正弦定理，，解得：，
故选：C.
20．中，角A、B、C所对的边为，若，则（ ）
A． B． C． D．
【答案】C
【解析】因为，所以由余弦定理得，，因为，所以，故选：C.
21．在中，，，，则的面积为 ．
【答案】
【解析】依题意可得，解得，又，所以，所以的面积为．故答案为：．
22．在中，角A，B，C的对边分别为a，b，c．若，则B等于（ ）
A． B． C． D．
【答案】C
【解析】在中，，设,由余弦定理得，
因为，所以，故选：C.
23．已知中，其内角A，B，C的对边分别为a，b，下列命题不正确的有（ ）
A．若，，，则
B．若，，，则
C．若A>B，则
D．若，，则外接圆半径为10
【答案】D
【解析】A.因为，，，由余弦定理得：，解得，故A正确；
B.因为，，，由正弦定理得：，解得，故B正确；
C.因为，所以，由正弦定理，得(R为外接圆半径)，
所以，故C正确；
D.因为，，设R为外接圆半径，由正弦定理，，所以，故D错误，故选：D.
24．在中，角的对边分别为，，则的形状是（ ）
A．等腰直角三角形B．直角三角形
C．等边三角形D．等腰三角形
【答案】D
【解析】由及正弦定理，得,在中，，所以,
所以，即，于是有，
因为所以所以,即，所以的形状是等腰三角形，故选：D.
25．在中，内角所对的边长分别为，且满足.
(1)求；
(2)若，求.
【答案】（1）；（2）
【解析】解：（1）因为，由正弦定理可得，，因为，所以，因为为三角形的内角，所以.
（2）因为，，，由正弦定理可得：，所以，因为为三角形的内角，所以，.x
－eq \f(φ,ω)
－eq \f(φ,ω)＋eq \f(π,2ω)
eq \f(π－φ,ω)
eq \f(3π,2ω)－eq \f(φ,ω)
eq \f(2π－φ,ω)
ωx＋φ
0
eq \f(π,2)
π
eq \f(3π,2)
2π
y＝Asin(ωx＋φ)
0
A
0
－A
0