2023年江苏省盐城市建湖县海南中学中考数学一模试卷

这是一份2023年江苏省盐城市建湖县海南中学中考数学一模试卷，共43页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）如图所示的平面图形能折叠成的长方体是（ ）
A．B．C．D．
2．（3分）不等式组的解集在数轴上表示为（ ）
A．B．
C．D．
3．（3分）“七巧板”是古代中国劳动人民的发明，被誉为“东方魔板”．图①是由该图形组成的正方形，图②是用该七巧板拼成的“和平鸽”图形，则飞镖落在和平鸽头部（阴影部分）的概率是（ ）
A．B．C．D．
4．（3分）中国奇书《易经》中记载，远古时期，人们通过在绳子上打结来计数，一位母亲在从右到左依次排列的绳子上打结，满5进1，孩子自出生后的天数是（ ）
A．10B．89C．165D．294
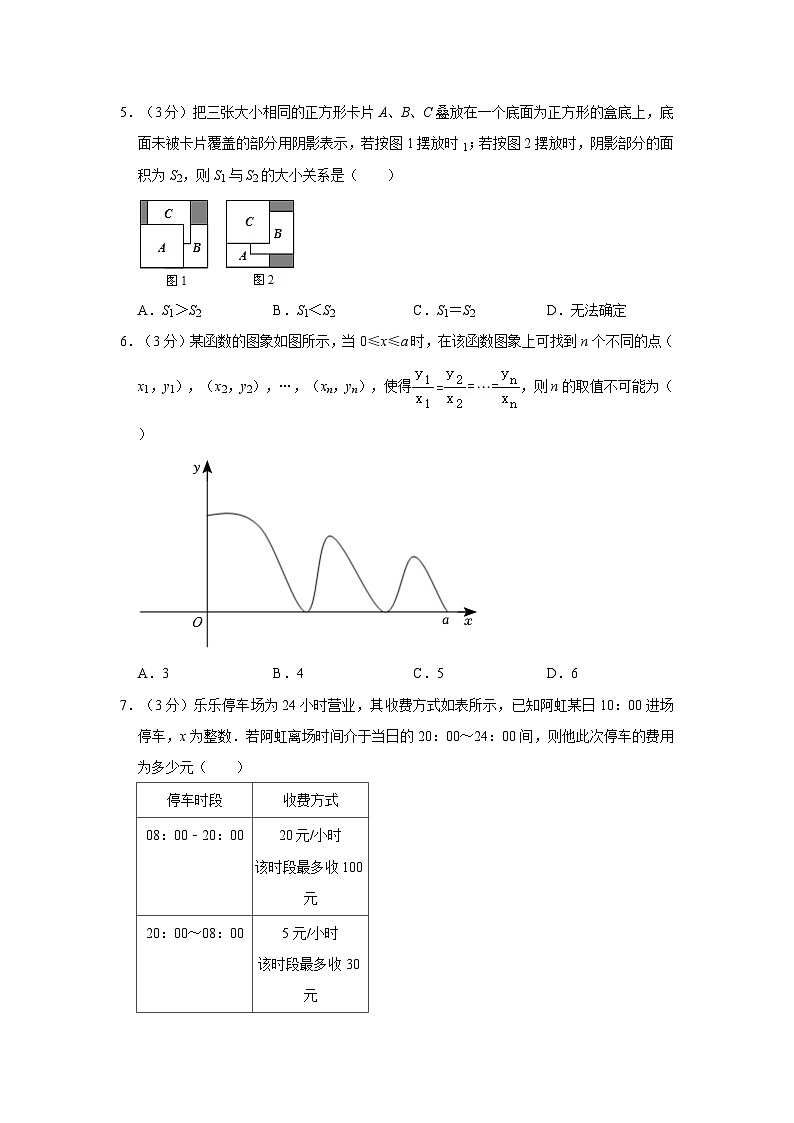
5．（3分）把三张大小相同的正方形卡片A、B、C叠放在一个底面为正方形的盒底上，底面未被卡片覆盖的部分用阴影表示，若按图1摆放时1；若按图2摆放时，阴影部分的面积为S2，则S1与S2的大小关系是（ ）
A．S1＞S2B．S1＜S2C．S1＝S2D．无法确定
6．（3分）某函数的图象如图所示，当0≤x≤a时，在该函数图象上可找到n个不同的点（x1，y1），（x2，y2），…，（xn，yn），使得，则n的取值不可能为（ ）
A．3B．4C．5D．6
7．（3分）乐乐停车场为24小时营业，其收费方式如表所示，已知阿虹某日10：00进场停车，x为整数．若阿虹离场时间介于当日的20：00～24：00间，则他此次停车的费用为多少元（ ）
A．5x+30B．5x+50C．5x+150D．5x+200
8．（3分）如图，在正方形ABCD中，点E，BC上的动点，且AF⊥DE，将△ABF沿AF翻折，得到△AMF，对角线BD交AF于点H，连接HM，DM，BM（ ）
①AF＝DE；②BM∥DE；③若CM⊥FM；④当点E运动到AB的中点，tan∠BHF＝2
A．①②③④⑤B．①②③⑤C．①②③D．①②⑤
二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把答案直接填写在答题卡相应位置上．）
9．（3分）已知，则a﹣20222＝ ．
10．（3分）下表是小红参加一次“阳光体育”活动比赛的得分情况：
评总分时，按跑步占50%，花样跳绳占30%，则小红的最终得分为 ．
11．（3分）对于任意实数a，b，我们定义新运算“*”：a*b＝a2+2ab﹣b2，例如3*5＝32+2×3×5﹣52＝14．若m，n是方程（x+2）*3＝0的两根，则+ ．
12．（3分）如图，在菱形ABCD中，∠DAB＝40°，以点A为圆心，AC长为半径作弧，连接CE，则∠AEC的度数是 ．
13．（3分）如图，在平面直角坐标系xOy中，△A′B′C′由△ABC绕点P旋转得到 ．
14．（3分）某日上午，甲、乙两车先后从A地出发沿同一条公路匀速前往B地，甲车8点出发（千米）随行驶时间t（小时）变化的图象．乙车9点出发（含12点和13点）追上甲车，则乙车的速度v（单位：千米/小时） ．
15．（3分）在如图所示的网格中，每个小正方形的边长为1，每个小正方形的顶点叫做格点，若图中扇形AOB是一个圆锥的侧面展开图，则该圆锥底面圆的半径为 ．
16．（3分）如图，点A的坐标是（a，0）（a＜0），点B是以OA为直径的⊙M上一动点，所有这样的点C组成的图形与直线y＝x﹣3有且只有一个公共点 ．
三、解答题（本大题共11小题，共102分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．）
17．（6分）阅读下面材料：
将边长分别为a，a+，a+2的正方形面积分别记为S1，S2，S3，S4．
则S2﹣S1＝（a+）2﹣a2
＝[（a+）+a]•[（a+）﹣a]
＝（2a+）•
＝b+2a
例如：当a＝1，b＝3时，S2﹣S1＝3+2
根据以上材料解答下列问题：
（1）当a＝1，b＝3时，S3﹣S2＝ ，S4﹣S3＝ ；
（2）当a＝1，b＝3时，把边长为a+nn+1，其中n是正整数，从（1）中的计算结果，你能猜出Sn+1﹣Sn等于多少吗？并证明你的猜想；
（3）当a＝1，b＝3时，令t1＝S2﹣S1，t2＝S3﹣S2，t3＝S4﹣S3，…，tn＝Sn+1﹣Sn，且T＝t1+t2+t3+…+t50，求T的值．
18．（6分）【探究】
若x满足（9﹣x）（x﹣4）＝4，求（4﹣x）2+（x﹣9）2的值．
设9﹣x＝a，x﹣4＝b，则（9﹣x）（x﹣4）＝ab＝4（9﹣x）+（x﹣4）＝5，
∴（9﹣x）2+（x﹣4）2＝a2+b2＝（a+b）2﹣2ab＝52﹣2×4＝17；
【应用】
请仿照上面的方法求解下面问题：
（1）若x满足（5﹣x）（x﹣2）＝2，求（5﹣x）2+（x﹣2）2的值；
【拓展】
（2）已知正方形ABCD的边长为x，E，F分别是AD、DC上的点，且AE＝1，长方形EMFD的面积是8，分别以MF、DF为边作正方形．
①MF＝ ，DF＝ ；（用含x的式子表示）
②求阴影部分的面积．
19．（8分）如图，是一个放置于水平桌面的平板支架的示意图，底座的高AB为5cm，点A是MN的中点，连杆BC、CD的长度分别为18.5cm和15cm，且连杆BC、CD与AB始终在同一平面内．
（1）求点C到水平桌面的距离；
（2）产品说明书提示，若点D与A的水平距离超过AN的长度，则该支架会倾倒．现将∠DCB调节为80°
（参考数据：tan20°≈0.36，ct20°≈2.75，sin20°≈0.34，cs20°≈0.94）
20．（8分）某工程由甲、乙两队合作6天完成，厂家需付甲、乙两队工程费8700元，乙、丙队合作10天完成，甲、丙两队合作5天完成全部工程的，厂家需付甲、丙两队工程费5500元．
（1）求甲、乙、丙各队单独完成全部工程，各需多少天．
（2）若工期要求不超过15天完成全部工程，则由哪个队单独完成此项工程所需的费用最少？请说明理由．
21．（8分）如图，直线l1：y＝kx+b与双曲线y＝（x＞0）交于A，B两点，与y轴交于点E，已知点A（1，3）（4，0）．
（1）求直线l1和双曲线的解析式；
（2）将△OCE沿直线l1翻折，点O落在第一象限内的点H处，求点H的坐标；
（3）如图，过点E作直线l2：y＝3x+4交x轴的负半轴于点F，在直线l2上是否存在点P，使得S△PBC＝S△OBC？若存在，请直接写出所有符合条件的点P的坐标；如果不存在
22．（10分）如图，△ABC为⊙O的内接三角形，BC为⊙O的直径（不与端点重合），作DG⊥BC，分别交AC、圆周于E、F，已知AG＝EG．
（1）求证：AG为⊙O的切线；
（2）已知AG＝2，填空：
①当四边形ABOF是菱形时，∠AEG＝ °；
②若OC＝2DC，△AGE为等腰直角三角形，则AB＝ ．
23．（10分）一辆快车从甲地出发驶向乙地，在到达乙地后，立即按原路原速返回到甲地，中途因故停车h后，两车距甲地的路程y km与慢车行驶时间x（h）之间的函数图象如图所示
（1）甲乙两地相距 km，快车行驶的速度是 km/h，图中括号内的数值是 ；
（2）求快车从乙地返回甲地的过程中，y与x的函数解析式；
（3）慢车出发多长时间，两车相距120km．
24．（10分）对于任意一个四位数m，若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍，则称这个四位数m为“共生数”．例如：m＝3507（5+0），所以3507是“共生数”；m＝4135（1+3），所以4135不是“共生数”．
（1）判断5313，6437是否为“共生数”？并说明理由；
（2）对于“共生数”n，当十位上的数字是千位上的数字的2倍，百位上的数字与个位上的数字之和能被9整除时（n）＝．求满足F（n）各数位上的数字之和是偶数的所有n．
25．（10分）【问题提出】如图1，用“圆规和无刻度的直尺”，作两条以O为圆心的圆弧将已知扇形的面积三等分．
【问题联思】如图2，已知线段MN，请你用“圆规和无刻度的直尺”作一个以MN为底边，并写出MN与MP的数量关系；
【问题再现】如图3，已知扇形OAB，请你用“圆规和无刻度的直尺”作两条以点O为圆心的圆弧（友情提醒：保留作图痕迹，并用黑笔描线加深）
26．（12分）在平面直角坐标系xOy中，已知点A在y轴正半轴上．
（1）如果四个点（0，0）、（0，2）、（1，1）、（﹣1，1）中恰有三个点在二次函数y＝ax2（a为常数，且a≠0）的图象上．
①a＝ ；
②如图1，已知菱形ABCD的顶点B、C、D在该二次函数的图象上，且AD⊥y轴；
③如图2，已知正方形ABCD的顶点B、D在该二次函数的图象上，点B、D在y轴的同侧，设点B、D的横坐标分别为m、n，试探究n﹣m是否为定值．如果是；如果不是，请说明理由．
（2）已知正方形ABCD的顶点B、D在二次函数y＝ax2（a为常数，且a＞0）的图象上，点B在点D的左侧，设点B、D的横坐标分别为m、n
27．（14分）（1）如图1，在矩形ABCD中，E为AD边上一点，若BE＝BC，过C作CF⊥BE交BE于点F，
①求证：△ABE≌△FCB；
②若S矩形ABCD＝20时，则BE•CF＝ ．
（2）如图2，在菱形ABCD中，csA＝，过E作EF⊥AD交AD于点F，若S菱形ABCD＝24时，求EF•BC的值．
（3）如图3，在平行四边形ABCD中，∠A＝60°，AD＝5，点E在CD上，点F为BC上一点，连接EF，若EF•EG＝7时，请直接写出AG的长．
参考答案与试题解析
一、选择题（本大题共8小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一个选项是正确的，请将正确选项的字母代号填涂在答题卡相应位置上）
1．（3分）如图所示的平面图形能折叠成的长方体是（ ）
A．B．C．D．
【解答】解：A、平面图形能折叠成的长方体正面的右邻面是阴影；
B、平面图形能折叠成的长方体上面的右邻面是阴影；
C、平面图形能折叠成的长方体正面是阴影，故C错误；
D、平面图形能折叠成的长方体上面的右邻面是阴影；
故选：D．
2．（3分）不等式组的解集在数轴上表示为（ ）
A．B．
C．D．
【解答】解：，
由①得，x＞1，
由②得，x≥2，
故此不等式组的解集为：x≥2．
在数轴上表示为：
．
故选：A．
3．（3分）“七巧板”是古代中国劳动人民的发明，被誉为“东方魔板”．图①是由该图形组成的正方形，图②是用该七巧板拼成的“和平鸽”图形，则飞镖落在和平鸽头部（阴影部分）的概率是（ ）
A．B．C．D．
【解答】解：由七巧板的特征可知，阴影部分的面积是七巧板面积的，
故飞镖落在和平鸽头部（阴影部分）的概率是．
故选：C．
4．（3分）中国奇书《易经》中记载，远古时期，人们通过在绳子上打结来计数，一位母亲在从右到左依次排列的绳子上打结，满5进1，孩子自出生后的天数是（ ）
A．10B．89C．165D．294
【解答】解：2×53+1×54+3×55+4×58＝294，
故选：D．
5．（3分）把三张大小相同的正方形卡片A、B、C叠放在一个底面为正方形的盒底上，底面未被卡片覆盖的部分用阴影表示，若按图1摆放时1；若按图2摆放时，阴影部分的面积为S2，则S1与S2的大小关系是（ ）
A．S1＞S2B．S1＜S2C．S1＝S2D．无法确定
【解答】解：设底面的正方形的边长为a，正方形卡片A，B，
由图1，得S1＝（a﹣b）（a﹣b）＝（a﹣b）2，
由图2，得S2＝（a﹣b）（a﹣b）＝（a﹣b）6，
∴S1＝S2．
故选：C．
6．（3分）某函数的图象如图所示，当0≤x≤a时，在该函数图象上可找到n个不同的点（x1，y1），（x2，y2），…，（xn，yn），使得，则n的取值不可能为（ ）
A．3B．4C．5D．6
【解答】解：设＝k，
则在该函数图象上n个不同的点（x1，y8），（x2，y2），…，（xn，yn）也都在函数y＝kx的图象上，
即：正比例函数y＝kx的图象与如图所示的图象的交点，
由图象可知，正比例函数y＝kx的图象与如图所示的图象的交点可能有3个或2个或3个或3个或5个．
故选：D．
7．（3分）乐乐停车场为24小时营业，其收费方式如表所示，已知阿虹某日10：00进场停车，x为整数．若阿虹离场时间介于当日的20：00～24：00间，则他此次停车的费用为多少元（ ）
A．5x+30B．5x+50C．5x+150D．5x+200
【解答】解：∵阿虹离场时间介于当日的20：00～24：00间，
∴阿虹的停车费为：100+5（x﹣10）＝（5x+50）元．
故选：B．
8．（3分）如图，在正方形ABCD中，点E，BC上的动点，且AF⊥DE，将△ABF沿AF翻折，得到△AMF，对角线BD交AF于点H，连接HM，DM，BM（ ）
①AF＝DE；②BM∥DE；③若CM⊥FM；④当点E运动到AB的中点，tan∠BHF＝2
A．①②③④⑤B．①②③⑤C．①②③D．①②⑤
【解答】解：∵四边形ABCD是正方形，
∴∠DAE＝∠ABF＝90°，DA＝AB，
∵AF⊥DE，
∴∠BAF+∠AED＝90°，
∵∠BAF+∠AFB＝90°，
∴∠AED＝∠BFA，
在△ABF和△DAE中，
，
∴△ABF≌△DAE（AAS），
∴AF＝DE．
故①正确；
∵将△ABF沿AF翻折，得到△AMF，
∴BM⊥AF，
∵AF⊥DE，
∴BM∥DE．
故②正确；
当CM⊥FM时，∠CMF＝90°，
∵∠AMF＝∠ABF＝90°，
∴∠AMF+∠CMF＝180°，即A，M，
∴∠MCF＝45°，
∴∠MFC＝90°﹣∠MCF＝45°，
由翻折的性质可得：∠HBF＝∠HMF＝45°，BF＝MF，
∴∠HMF＝∠MFC，∠HBC＝∠MFC，
∴BC∥MH，HB∥MF，
∴四边形BHMF是平行四边形，
∵BF＝MF，
∴平行四边形BHMF是菱形，故③正确；
当点E运动到AB的中点，如图，
设正方形ABCD的边长为2a，则AE＝BF＝a，
在Rt△AED中，
，
∵∠AHD＝∠FHB，∠ADH＝∠FBH＝45°，
∴△AHD∽△FHB，
∴，
∴．
∵∠AGE＝∠ABF＝90°，∠EAG＝∠FAB，
∴△AGE∽△ABF，
∴，
∴，，
∴，．
∵∠BHF＝∠DHA，
∴在Rt△DGH中，
，
故④错误；
由题意得：△ABF≌△AMF，
∴∠EAG＝∠PAG，
在△EAG和PAG中，
，
∴△EAG≌PAG（ASA），
∴EG＝PG，
∴EG＝EP．
∵AD∥BC，
∴△AHD∽△FHB，
∴．
∵AD＝AB，
∴．
∵∠AGE＝∠ABF＝90°，∠EAG＝∠FAB，
∴△EAG∽△FAB，
∴，
∴，
∴EG•DH＝AG•BH，
∴EP•DH＝AG•BH，
∴EP•DH＝2AG•BH，
故⑤正确．
综上分析可知，正确的是①②③⑤．
故选：B．
二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把答案直接填写在答题卡相应位置上．）
9．（3分）已知，则a﹣20222＝ 2023 ．
【解答】解：∵有意义，
∴a﹣2023≥0，即a≥2023，
∴，
∴，
∴a﹣2023＝20222，
∴a﹣20228＝2023，
故答案为：2023．
10．（3分）下表是小红参加一次“阳光体育”活动比赛的得分情况：
评总分时，按跑步占50%，花样跳绳占30%，则小红的最终得分为 83分 ．
【解答】解：小红的最终得分为：90×50%+80×30%+70×20%＝83（分）．
故答案为：83分．
11．（3分）对于任意实数a，b，我们定义新运算“*”：a*b＝a2+2ab﹣b2，例如3*5＝32+2×3×5﹣52＝14．若m，n是方程（x+2）*3＝0的两根，则+ ．
【解答】解：由题意得（x+2）*3＝7即为（x+2）2+3（x+2）﹣9＝6，
化简得x2+10x+7＝6，
∵m，n是该方程的两根，
∴m+n＝﹣10，mn＝7，
∴+＝＝，
故答案为：．
12．（3分）如图，在菱形ABCD中，∠DAB＝40°，以点A为圆心，AC长为半径作弧，连接CE，则∠AEC的度数是 10°或80° ．
【解答】解：以点A为圆心，AC长为半径作弧，如图所示，
在菱形ABCD中，∠DAC＝∠BAC，
∵∠DAB＝40°，
∴∠DAC＝20°，
∵AC＝AE，
∴∠AEC＝（180°﹣20°）÷2＝80°，
∵AE′＝AC，
∴∠AE′C＝∠ACE′＝10°，
综上所述，∠AEC的度数是10°或80°，
故答案为：10°或80°．
13．（3分）如图，在平面直角坐标系xOy中，△A′B′C′由△ABC绕点P旋转得到 （1，﹣1） ．
【解答】解：连接AA′、CC′，
作线段AA′的垂直平分线MN，作线段CC′的垂直平分线EF，
直线MN和直线EF的交点为P，点P就是旋转中心．
∵直线MN为：x＝1，设直线CC′为y＝kx+b，
∴，
∴直线CC′为y＝x+，
∵直线EF⊥CC′，经过CC′中点（，），
∴直线EF为y＝﹣3x+8，
由得，
∴P（4，﹣1）．
（本题可以用图象法，直接得出P坐标）．
故答案为（1，﹣5）．
14．（3分）某日上午，甲、乙两车先后从A地出发沿同一条公路匀速前往B地，甲车8点出发（千米）随行驶时间t（小时）变化的图象．乙车9点出发（含12点和13点）追上甲车，则乙车的速度v（单位：千米/小时） 75≤v≤80 ．
【解答】解：根据图象可得，甲的速度为：60÷1＝60（千米/时），
由题意，得，
解得75≤v≤80，
故答案为：75≤v≤80．
15．（3分）在如图所示的网格中，每个小正方形的边长为1，每个小正方形的顶点叫做格点，若图中扇形AOB是一个圆锥的侧面展开图，则该圆锥底面圆的半径为 ．
【解答】解：设该圆锥底面圆的半径为r．
∵每个小方格都是边长为1的正方形，
∴AO＝＝8，
由图形可知∠AOB＝90°，
∴＝2πr，
∴r＝．
故答案为：．
16．（3分）如图，点A的坐标是（a，0）（a＜0），点B是以OA为直径的⊙M上一动点，所有这样的点C组成的图形与直线y＝x﹣3有且只有一个公共点 ﹣ ．
【解答】解：如图，连接BM，设直线y＝﹣，4），﹣3），
∵AB＝BC，AM＝OM，
∴OC＝2BM＝﹣a，
∴点C的运动轨迹是以O为圆心﹣a为半径的圆，当⊙O与直线y＝﹣，点C组成的图形与直线y＝﹣，设切点为G．
∵OG⊥EF，点E（﹣4，点F（0，
∴EF＝＝5，
∴•OE•OF＝，
∴OG＝，
∴a＝﹣，
故答案为：﹣．
三、解答题（本大题共11小题，共102分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．）
17．（6分）阅读下面材料：
将边长分别为a，a+，a+2的正方形面积分别记为S1，S2，S3，S4．
则S2﹣S1＝（a+）2﹣a2
＝[（a+）+a]•[（a+）﹣a]
＝（2a+）•
＝b+2a
例如：当a＝1，b＝3时，S2﹣S1＝3+2
根据以上材料解答下列问题：
（1）当a＝1，b＝3时，S3﹣S2＝ 9+2 ，S4﹣S3＝ 15+2 ；
（2）当a＝1，b＝3时，把边长为a+nn+1，其中n是正整数，从（1）中的计算结果，你能猜出Sn+1﹣Sn等于多少吗？并证明你的猜想；
（3）当a＝1，b＝3时，令t1＝S2﹣S1，t2＝S3﹣S2，t3＝S4﹣S3，…，tn＝Sn+1﹣Sn，且T＝t1+t2+t3+…+t50，求T的值．
【解答】解：S3﹣S2＝（a+3）2﹣（a+）2
＝a4+4a+4b﹣a7﹣2a﹣b
＝2a+6b，
当a＝1，b＝3时，S8﹣S2＝9+6；
S4﹣S8＝（a+3）2﹣（a+2）2＝a2+7a+9b﹣a2﹣5a﹣4b
＝2a+8b，
当a＝1，b＝3时，S4﹣S3＝15+2；
故答案为：9+2；15+2；
（2）Sn+7﹣Sn＝6n﹣3+7；
证明：Sn+1﹣Sn
＝（3+n）2﹣[2+（n﹣1）]7
＝[2+（2n﹣6）]×
＝5（2n﹣1）+7
＝6n﹣4+2；
（3）当a＝6，b＝3时1+t7+t3+…+t50
＝S2﹣S6+S3﹣S2+S7﹣S3…+S51﹣S50
＝S51﹣S1
＝（4+50）2﹣7
＝7500+100．
18．（6分）【探究】
若x满足（9﹣x）（x﹣4）＝4，求（4﹣x）2+（x﹣9）2的值．
设9﹣x＝a，x﹣4＝b，则（9﹣x）（x﹣4）＝ab＝4（9﹣x）+（x﹣4）＝5，
∴（9﹣x）2+（x﹣4）2＝a2+b2＝（a+b）2﹣2ab＝52﹣2×4＝17；
【应用】
请仿照上面的方法求解下面问题：
（1）若x满足（5﹣x）（x﹣2）＝2，求（5﹣x）2+（x﹣2）2的值；
【拓展】
（2）已知正方形ABCD的边长为x，E，F分别是AD、DC上的点，且AE＝1，长方形EMFD的面积是8，分别以MF、DF为边作正方形．
①MF＝ x﹣1 ，DF＝ x﹣3 ；（用含x的式子表示）
②求阴影部分的面积．
【解答】解：（1）设5﹣x＝a，x﹣2＝b，
则（7﹣x）（x﹣2）＝ab＝2，a+b＝（4﹣x）+（x﹣2）＝3，
∴（5﹣x）2+（x﹣2）2
＝a2+b2
＝（a+b）8﹣2ab
＝35﹣2×2
＝6﹣4
＝5；
（2）①∵四边形EMFD是长方形，AE＝7，
∴AD＝CD＝BC＝x，DE＝MF，
∴MF＝DE＝AD﹣AE＝x﹣1，
DF＝CD﹣CF＝x﹣3，
故答案为：x﹣2，x﹣3；
②∵长方形EMFD的面积是8，
∴MF•DF＝（x﹣8）（x﹣3）＝8，
阴影部分的面积＝MF6﹣DF2＝（x﹣1）5﹣（x﹣3）2．
设x﹣5＝a，x﹣3＝b，a﹣b＝（x﹣1）﹣（x﹣2）＝2，
∴（a+b）2＝（a﹣b）2+4ab＝28+4×8＝36，
∴a+b＝±2，
又∵a+b＞0，
∴a+b＝6，
∴（x﹣7）2﹣（x﹣3）3＝a2﹣b2＝（a+b）（a﹣b）＝2×2＝12．
即阴影部分的面积12．
19．（8分）如图，是一个放置于水平桌面的平板支架的示意图，底座的高AB为5cm，点A是MN的中点，连杆BC、CD的长度分别为18.5cm和15cm，且连杆BC、CD与AB始终在同一平面内．
（1）求点C到水平桌面的距离；
（2）产品说明书提示，若点D与A的水平距离超过AN的长度，则该支架会倾倒．现将∠DCB调节为80°
（参考数据：tan20°≈0.36，ct20°≈2.75，sin20°≈0.34，cs20°≈0.94）
【解答】解：作CE⊥NM于E，BF⊥CE于F，
∵∠CBF＝∠CBA﹣∠FBA＝150°﹣90°＝60°，
∴sin∠CBF＝sin60°＝＝，
∴CF＝（cm），
∴CE＝CF+EF＝CF+AB＝（cm）．
∴点C到水平桌面的距离是cm；
（2）作DK⊥FB交FB延长线于K，作CH⊥DK于H，
∵∠DCH＝∠DCB﹣∠HCB＝80°＝60°＝20°，
∴cs∠DCH＝cs20°＝≈0.94，
∴FK＝CH＝14.4（cm），
∵∠BCF＝30°，
∴BF＝BC＝8.25（cm），
∴BK＝FK﹣BF＝4.85（cm），
∴AN＝MN＝5（cm），
∴此时支架不会倾倒．
20．（8分）某工程由甲、乙两队合作6天完成，厂家需付甲、乙两队工程费8700元，乙、丙队合作10天完成，甲、丙两队合作5天完成全部工程的，厂家需付甲、丙两队工程费5500元．
（1）求甲、乙、丙各队单独完成全部工程，各需多少天．
（2）若工期要求不超过15天完成全部工程，则由哪个队单独完成此项工程所需的费用最少？请说明理由．
【解答】解：（1）设甲、乙、丙各队完成这项工程所需要时间分别为x天、z天．
根据题意，得：
解得：x＝10，y＝15．
经检验：x＝10，y＝15，且符合题意．
答：甲、乙、丙各队单独完成全部工程分别需10天、30天．
（2）设甲、乙、丙各队工作一天、b元．
根据题意得：解得．
丙队工作30天首先排除；
甲队完成项目所需费用为ax＝8000元；
乙队完成项目所需费用为by＝650×15＝9750元．
答：甲队单独完成此项工程所需的费用最少．
21．（8分）如图，直线l1：y＝kx+b与双曲线y＝（x＞0）交于A，B两点，与y轴交于点E，已知点A（1，3）（4，0）．
（1）求直线l1和双曲线的解析式；
（2）将△OCE沿直线l1翻折，点O落在第一象限内的点H处，求点H的坐标；
（3）如图，过点E作直线l2：y＝3x+4交x轴的负半轴于点F，在直线l2上是否存在点P，使得S△PBC＝S△OBC？若存在，请直接写出所有符合条件的点P的坐标；如果不存在
【解答】解：（1）将A（1，3），4）代入y＝kx+b，得，
∴直线l3的解析式为y＝﹣x+4．
将A（1，8）代入y＝，得m＝3，
∴双曲线的解析式为y＝（x＞4）；
（2）将x＝0代入y＝﹣x+4，得y＝6，
∴E（0，4）．
∴△COE是等腰直角三角形．
∴∠OCE＝∠OEC＝45°，OC＝OE＝4．
由翻折得△CEH≌△CEO，
∴∠COE＝∠CHE＝∠OCH＝90°．
∴四边形OCHE是正方形．
∴H（4，4）；
（3）存在，理由：
如图，过点O作直线m∥BC交直线l2于点P′，
在x轴取点H，使OC＝CH（即等间隔）2于点P，
S△PBC＝S△OBC，根据同底等高的两个三角形面积相等，则点P（P′）为所求点．
直线BC表达式中的k值为﹣1，则直线m，
故直线m的表达式为：y＝﹣x①，
直线l7的表达式为：y＝3x+4②，
联立①②并解得：x＝﹣7，y＝1，1）；
设直线n的表达式为：y＝﹣x+s，而点H（2，
将点H的坐标代入上式并解得：s＝8，
故直线n的表达式为：y＝﹣x+8③，
联立②③并解得：x＝6，y＝7，
故点P的坐标为（1，3）；
综上，点P的坐标为（﹣1，7）．
22．（10分）如图，△ABC为⊙O的内接三角形，BC为⊙O的直径（不与端点重合），作DG⊥BC，分别交AC、圆周于E、F，已知AG＝EG．
（1）求证：AG为⊙O的切线；
（2）已知AG＝2，填空：
①当四边形ABOF是菱形时，∠AEG＝ 60 °；
②若OC＝2DC，△AGE为等腰直角三角形，则AB＝ 4 ．
【解答】（1）证明：连接OA．
∵OA＝OC，
∴∠OAC＝∠OCA，
∵GA＝GE，
∴∠GAE＝∠GEA，
∵DG⊥BC，
∴∠EDC＝90°，
∴∠OCA+∠DEC＝90°，
∵∠CED＝∠GEA＝∠GAE，
∴∠OAC+∠GAE＝90°，
∴∠OAG＝90°，
∴OA⊥AG，
∴AG是⊙O的切线．
（2）①如图2中，连接OA，OF．
∵四边形ABOF是 菱形，
∴AB＝BO＝OF＝AF＝OA，
∴△ABO是等边三角形，
∴∠B＝60°，
∵BC是直径，
∴∠BAC＝90°
∴∠ACB＝90°﹣60°＝30°，
∵ED⊥BC，
∴∠DEC＝90°﹣∠ACB＝60°，
∴∠AEG＝∠DEC＝60°．
故答案为60．
②如图3中，
连接OA．
∵△AGE是等腰直角三角形，
∴∠AEG＝∠DEC＝∠DCE＝45°，
∴△EDC，△ABC都是等腰直角三角形，
∵OB＝OC，
∴AO⊥OC，
∴∠AOD＝∠ODG＝∠G＝90°，
∴四边形AODG是矩形，
∴AG＝OD＝5，
∴OC＝2OD＝4，
∴BC＝2OC＝8，
∴AB＝AC＝4，
故答案为4．
23．（10分）一辆快车从甲地出发驶向乙地，在到达乙地后，立即按原路原速返回到甲地，中途因故停车h后，两车距甲地的路程y km与慢车行驶时间x（h）之间的函数图象如图所示
（1）甲乙两地相距 400 km，快车行驶的速度是 100 km/h，图中括号内的数值是 7 ；
（2）求快车从乙地返回甲地的过程中，y与x的函数解析式；
（3）慢车出发多长时间，两车相距120km．
【解答】解：（1）由图象可知：甲乙两地相距400km，快车行驶的速度为（400﹣100）÷3＝100km/h，
故答案为：400，100，7；
（2）由图象可知：B（3，400）和A（7，
设直线BA的函数解析式为：y＝kx+b，
把B（3，400）和A（4，
解之得，
∴快车从乙地返回甲地的过程中，y与x的函数解析式为y＝﹣100x+700；
（3）由图象可知：快车比慢车早出发1小时，
∴慢车的速度为：千米/小时，
设慢车出发x小时与快车相距120千米，
①快车从甲地开往乙地，由题意得：100（x+1）＝80x+120，
解之得：x＝1，
②快车从乙地返回甲地与慢车相遇前，由题意得：100（x+3）﹣400+120+80，
解之得：，
③快车从乙地返回甲地与慢车相遇后，由题意得：，
解之得：，
综上可知慢车出发1小时或小时或，两车相距120km．
24．（10分）对于任意一个四位数m，若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍，则称这个四位数m为“共生数”．例如：m＝3507（5+0），所以3507是“共生数”；m＝4135（1+3），所以4135不是“共生数”．
（1）判断5313，6437是否为“共生数”？并说明理由；
（2）对于“共生数”n，当十位上的数字是千位上的数字的2倍，百位上的数字与个位上的数字之和能被9整除时（n）＝．求满足F（n）各数位上的数字之和是偶数的所有n．
【解答】解：（1）5313是“共生数”，6437不是“共生数”，
∵5+3＝4×（3+1），
∴5313是“共生数”，
∵4+7≠2×（2+4），
∴6437不是“共生数”；
（2）∵n是“共生数”，根据题意，
设n的千位上的数字为a，则十位上的数字为2a，
设n的百位上的数字为b，
∵个位和百位都是5﹣9的数字，
∴个位上的数字为9﹣b，且3﹣b＞b，
∴0≤b≤4，
∴n＝1000a+100b+20a+6﹣b，
∴F（n）＝＝340a+33b+3，
由于n是“共生数”，
∴a+9﹣b＝2×（7a+b），
即a+b＝3，
可能的情况有：
，
当a＝1，b＝3时，则F（n）的值为409，舍去，
当a＝2，b＝1时，则F（n）的值为716，
当a＝7，b＝0时，则F（n）的值为1023，
∴n的值是2148或3069．
25．（10分）【问题提出】如图1，用“圆规和无刻度的直尺”，作两条以O为圆心的圆弧将已知扇形的面积三等分．
【问题联思】如图2，已知线段MN，请你用“圆规和无刻度的直尺”作一个以MN为底边，并写出MN与MP的数量关系；
【问题再现】如图3，已知扇形OAB，请你用“圆规和无刻度的直尺”作两条以点O为圆心的圆弧（友情提醒：保留作图痕迹，并用黑笔描线加深）
【解答】解：[问题联思]如图所示，分别以M，MN为半径作圆，则三角形MNQ为等边三角形，MN的垂直平分线，则△PMN即为所求；
∴MN＝2PN•cs30°＝MP；
[问题再现]同上方法作以OA为底边，底角为30°的等腰三角形COA，则OA＝，
则∠ODA＝60°，设OD＝a，
以O为圆心OD为半径，作弧，
连接DF，则，
以O为圆心DF为半径，作弧，
设∠AOB＝n°，
∴扇形OFN的面积为，
扇形OGM的面积为，
扇形OAB的面积为，
∴弧，，即为所求．
26．（12分）在平面直角坐标系xOy中，已知点A在y轴正半轴上．
（1）如果四个点（0，0）、（0，2）、（1，1）、（﹣1，1）中恰有三个点在二次函数y＝ax2（a为常数，且a≠0）的图象上．
①a＝ 1 ；
②如图1，已知菱形ABCD的顶点B、C、D在该二次函数的图象上，且AD⊥y轴；
③如图2，已知正方形ABCD的顶点B、D在该二次函数的图象上，点B、D在y轴的同侧，设点B、D的横坐标分别为m、n，试探究n﹣m是否为定值．如果是；如果不是，请说明理由．
（2）已知正方形ABCD的顶点B、D在二次函数y＝ax2（a为常数，且a＞0）的图象上，点B在点D的左侧，设点B、D的横坐标分别为m、n
【解答】解：（1）①在y＝ax2中，令x＝0得y＝8，
∴（0，0）在二次函数y＝ax4（a为常数，且a≠0）的图象上，2）不在二次函数y＝ax6（a为常数，且a≠0）的图象上，
∵四个点（0，2），2），1），5）中恰有三个点在二次函数y＝ax2（a为常数，且a≠0）的图象上，
∴二次函数y＝ax3（a为常数，且a≠0）的图象上的三个点是（0，（6，（﹣1，
把（1，5）代入y＝ax2得：a＝1，
故答案为：7；
②设BC交y轴于E，如图：
设菱形的边长为2t，则AB＝BC＝CD＝AD＝2t，
∵B，C关于y轴对称，
∴BE＝CE＝t，
∴B（﹣t，t3），
∴OE＝t2，
∵AE＝＝t，
∴OA＝OE+AE＝t2+t，
∴D（2t，t2+t），
把D（2t，t2+t）代入y＝x2得：
t2+t＝4t2，
解得t＝或t＝0（舍去），
∴菱形的边长为；
③n﹣m是为定值，理由如下：
过B作BF⊥y轴于F，过D作DE⊥y轴于E
∵点B、D的横坐标分别为m、n，
∴B（m，m7），D（n，n2），
∴BF＝m，OF＝m2，DE＝n，OE＝n4，
∵四边形ABCD是正方形，
∴∠DAB＝90°，AD＝AB，
∴∠FAB＝90°﹣∠EAD＝∠EDA，
∵∠AFB＝∠DEA＝90°，
∴△ABF≌△DAE（AAS），
∴BF＝AE，AF＝DE，
∴m＝n2﹣AF﹣m2，AF＝n，
∴m＝n5﹣n﹣m2，
∴m+n＝（n﹣m）（n+m），
∵点B、D在y轴的同侧，
∴m+n≠0，
∴n﹣m＝5；
（2）过B作BF⊥y轴于F，过D作DE⊥y轴于E，
∵点B、D的横坐标分别为m、n，
∴B（m，am2），D（n2），
①当B，D在y轴左侧时
∴BF＝﹣m，OF＝am7，DE＝﹣n，OE＝an2，
同理可得△ABF≌△DAE（AAS），
∴BF＝AE，AF＝DE，
∴﹣m＝am2﹣AF﹣an5，AF＝﹣n，
∴﹣m＝am2+n﹣an2，
∴m+n＝a（n﹣m）（n+m），
∵m+n≠6，
∴n﹣m＝；
②当B在y轴左侧，D在y轴右侧时
∴BF＝﹣m，OF＝am2，DE＝n，OE＝an5，
同理可得△ABF≌△DAE（AAS），
∴BF＝AE，AF＝DE，
∴﹣m＝am2+AF﹣an2，AF＝n，
∴﹣m＝am8+n﹣an2，
∴m+n＝a（n+m）（n﹣m），
∴m+n＝0或n﹣m＝；
③当B，D在y轴右侧时
∴BF＝m，OF＝am2，DE＝n，OE＝an2，
同理可得△ABF≌△DAE（AAS），
∴BF＝AE，AF＝DE，
∴m＝an2﹣AF﹣am2，AF＝n，
∴m＝an2﹣n﹣am2，
∴m+n＝a（n+m）（n﹣m），
∵m+n≠0
∴n﹣m＝；
综上所述，m、n满足的等量关系式为m+n＝7或n﹣m＝．
27．（14分）（1）如图1，在矩形ABCD中，E为AD边上一点，若BE＝BC，过C作CF⊥BE交BE于点F，
①求证：△ABE≌△FCB；
②若S矩形ABCD＝20时，则BE•CF＝ 20 ．
（2）如图2，在菱形ABCD中，csA＝，过E作EF⊥AD交AD于点F，若S菱形ABCD＝24时，求EF•BC的值．
（3）如图3，在平行四边形ABCD中，∠A＝60°，AD＝5，点E在CD上，点F为BC上一点，连接EF，若EF•EG＝7时，请直接写出AG的长．
【解答】解：（1）①∵四边形ABCD是矩形，则∠A＝∠ABC＝90°，
∴∠ABE+∠CBF＝90°，
又∵CF⊥BC，
∴∠FCB+∠CBF＝90°，∠CFB＝∠A＝90°，
∴∠FCB＝∠ABE，
又∵BC＝BE，
∴△ABE≌△FCB（AAS）；
②由①可得∠FCB＝∠ABE，∠CFB＝∠A＝90°，
∴△ABE∽△FCB．
∴＝，
又∵S矩形ABCD＝AB•CD＝20，
∴BE•CF＝AB•BC＝20，
 （2）∵在菱形ABCD中，，
∴AD∥BC，AB＝BC，
∵CE⊥AB，∠CEB＝90°，
∴，
∴，
∴，
∵EF⊥AD，CE⊥AB，
∴∠AFE＝∠BEC＝90°，
又∵∠CBE＝∠A，
∴△AFE∽△BEC，
∴，
∴EF•BC＝AE•CE＝AB×CE＝S菱形ABCD＝×24＝32；
（3）①当点G在AD边上时，如图所示，连接GF，
∵平行四边形ABCD中，AB＝6，
∴CD＝AB＝2，
 DE＝DC﹣EC＝6﹣2＝6，
∵DM∥FC，
∴△EDM∽△ECF，
∴，
＝＝2，
∴S△MGE＝2S△EFG＝EF•EG＝7，
 在Rt△DEH 中，∠HDE＝∠A＝60°，
则 ，，
∴，
∴MG＝7，
∵GE⊥EF，EH⊥MG，
∴tan∠MEH＝tan∠HGE，
∵，
∴HE2＝HM•HG，
设AG＝a，则GD＝AD﹣AG＝4﹣a，
GH＝GD+HD＝5﹣a+2＝2﹣a，HM＝GM﹣GH＝7﹣（7﹣a）＝a，
（5）2＝a（8﹣a），
解得：a＝3或a＝4，
即AG＝8或AG＝4，
②当G点在AB边上时，如图所示，
连接GF，延长GE交BC的延长线于点M，则GN∥BC，
设AG＝x，则 DN＝AG＝x，
∵GN∥CM，
∴△ENG∽△ECM，
∴，
∴，
∴，
∵EF•，
∴，
过点E作EH⊥BC于点H，
在Rt△EHC中，EC＝2，
∴，CH＝7，
∴，
则 ，
∴，
∴，，
∵∠MEF＝∠EHM＝90°，∠FEH＝90°﹣∠MEH＝∠M，
∴tan∠FEH＝tan∠M，
即 ，
∴EH2＝FH•HM，
即 ，
解得： x2＝8 （舍去），
即 ；
③当G点在BC边上时，如图所示，
过点B作BT⊥DC于点T，
在Rt△BTC 中，，
，
，
 EF•EG＝8，
∴，
∵，
∴G点不可能在BC边上，
④当G点在CD上时，EF⊥GE，舍去，
综上所述，AG的长为3或4或 ．停车时段
收费方式
08：00﹣20：00
20元/小时
该时段最多收100元
20：00～08：00
5元/小时
该时段最多收30元
若进场与离场时间不在同一时段，则两时段分别计费
项目
跑步
花样跳绳
跳绳
得分
90
80
70
停车时段
收费方式
08：00﹣20：00
20元/小时
该时段最多收100元
20：00～08：00
5元/小时
该时段最多收30元
若进场与离场时间不在同一时段，则两时段分别计费
项目
跑步
花样跳绳
跳绳
得分
90
80
70