2023—2024学年下学期初中数学北师大新版七年级期中必刷常考题之整式的乘法

这是一份2023—2024学年下学期初中数学北师大新版七年级期中必刷常考题之整式的乘法，共15页。试卷主要包含了已知，计算等内容，欢迎下载使用。
1．已知：（2x+1）（x﹣3）＝2x2+px+q，则p，q的值分别为（ ）
A．5，3B．5，﹣3C．﹣5，3D．﹣5，﹣3
2．下列算式计算结果为x2﹣x﹣12的是（ ）
A．（x+3）（x﹣4）B．（x﹣3）（x+4）
C．（x﹣3）（x﹣4）D．（x+3）（x+4）
3．若（2x+m）（x﹣3）的展开式中不含x项，则实数m的值为（ ）
A．﹣6B．0C．3D．6
4．某同学在计算﹣3x加上一个多项式时错将加法做成了乘法，得到的答案是3x3﹣3x2+3x，由此可以推断出正确的计算结果是（ ）
A．﹣x2﹣2x﹣1B．x2+2x﹣1C．﹣x2+4x﹣1D．x2﹣4x+1
5．通过计算比较图1，图2中阴影部分的面积，可以验证的计算式子是（ ）
A．a（b﹣x）＝ab﹣ax
B．b（a﹣x）＝ab﹣bx
C．（a﹣x）（b﹣x）＝ab﹣ax﹣bx
D．（a﹣x）（b﹣x）＝ab﹣ax﹣bx+x2
二．填空题（共5小题）
6．已知x+y＝3，xy＝1，则（x﹣2）（y﹣2）＝ ．
7．若x﹣y＝3且xy＝1，则代数式（1+x）（y﹣1）的值等于 ．
8．计算：2a2•（﹣3a）＝ ．
9．计算：a2b•ab﹣1＝ ．
10．对于实数a，b，c，d，规定一种运算ad﹣bc，如1×（﹣2）﹣0×2＝﹣2，那么当27时，则x＝ ．
三．解答题（共5小题）
11．老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下：
×（xy）＝3x2y﹣xy2xy
（1）求所捂的多项式；
（2）若x，y，求所捂多项式的值．
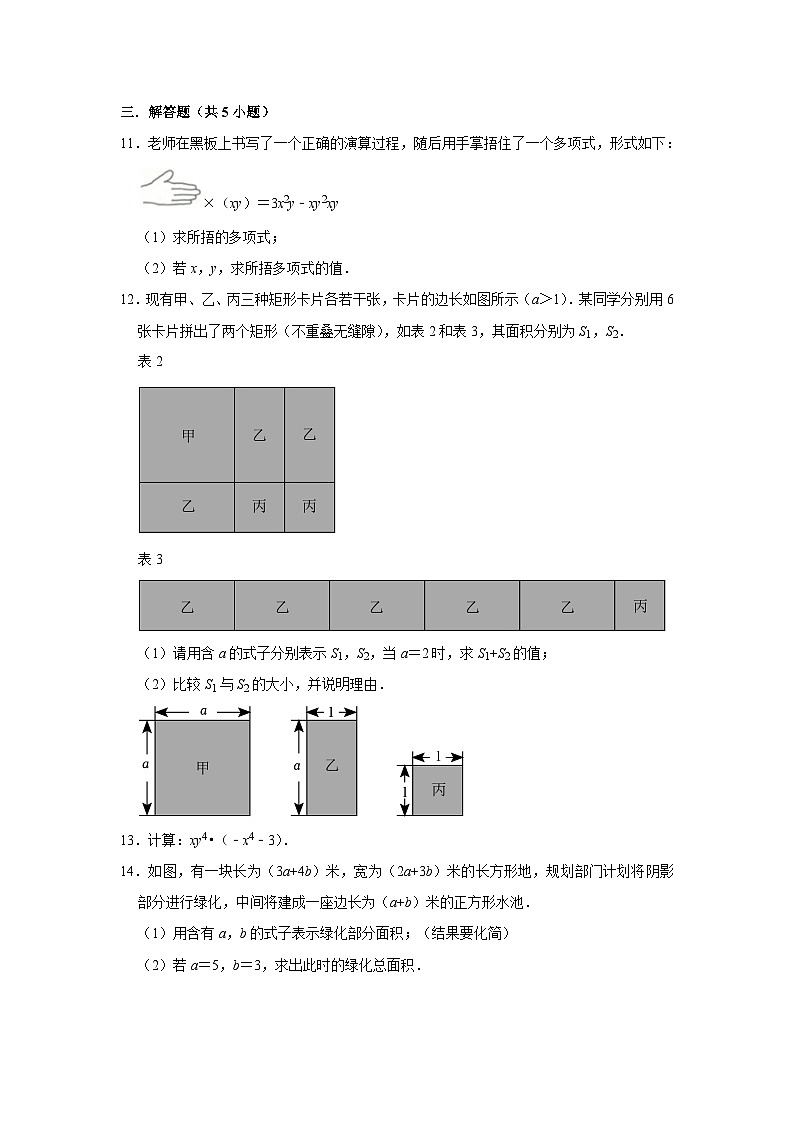
12．现有甲、乙、丙三种矩形卡片各若干张，卡片的边长如图所示（a＞1）．某同学分别用6张卡片拼出了两个矩形（不重叠无缝隙），如表2和表3，其面积分别为S1，S2．
表2
表3
（1）请用含a的式子分别表示S1，S2，当a＝2时，求S1+S2的值；
（2）比较S1与S2的大小，并说明理由．
13．计算：xy4•（﹣x4﹣3）．
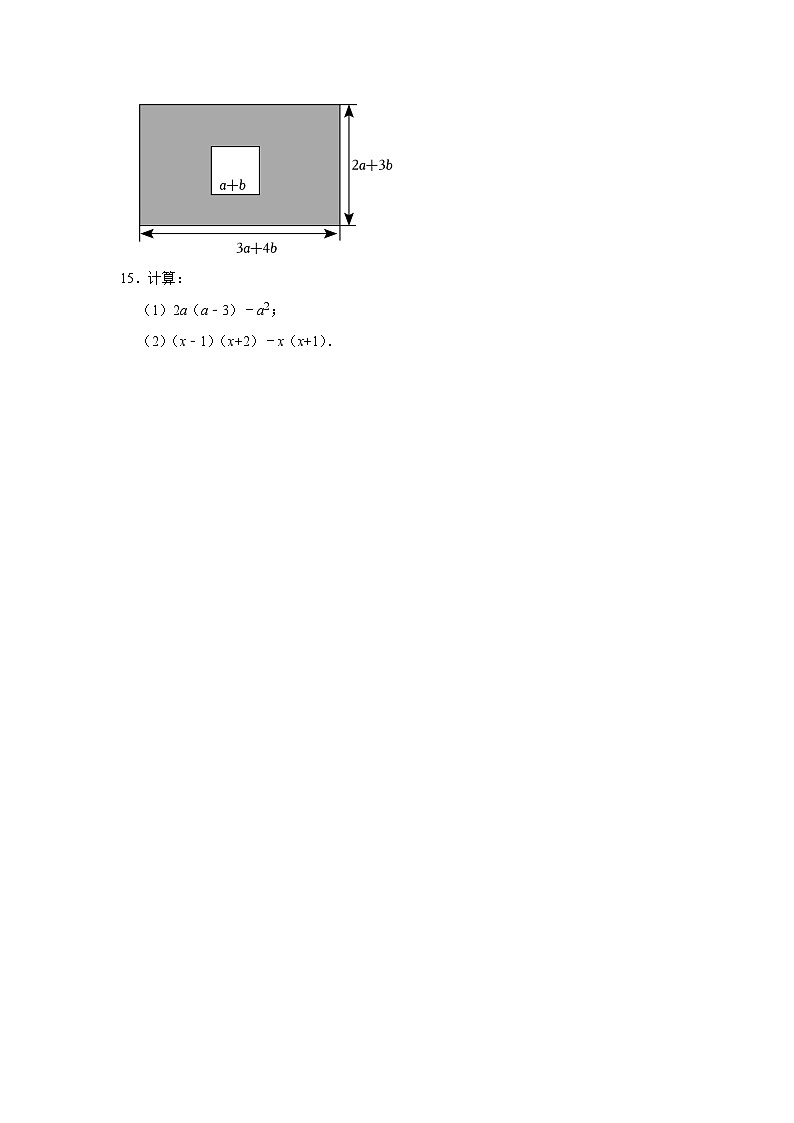
14．如图，有一块长为（3a+4b）米，宽为（2a+3b）米的长方形地，规划部门计划将阴影部分进行绿化，中间将建成一座边长为（a+b）米的正方形水池．
（1）用含有a，b的式子表示绿化部分面积；（结果要化简）
（2）若a＝5，b＝3，求出此时的绿化总面积．
15．计算：
（1）2a（a﹣3）﹣a2；
（2）（x﹣1）（x+2）﹣x（x+1）．
2023—2024学年下学期初中数学北师大新版七年级期中必刷常考题之整式的乘法
参考答案与试题解析
一．选择题（共5小题）
1．已知：（2x+1）（x﹣3）＝2x2+px+q，则p，q的值分别为（ ）
A．5，3B．5，﹣3C．﹣5，3D．﹣5，﹣3
【考点】多项式乘多项式．
【专题】计算题；整式；运算能力．
【答案】D
【分析】由（2x+1）（x﹣3）＝2x2﹣5x﹣3结合（2x+1）（x﹣3）＝2x2+px+q，即可得出p、q的值．
【解答】解：（2x+1）（x﹣3）＝2x2﹣6x+x﹣3＝2x2﹣5x﹣3，
∵（2x+1）（x﹣3）＝2x2+px+q，
∴p＝﹣5，q＝﹣3，
故选：D．
【点评】本题考查了多项式乘多项式，解题的关键是掌握多项式乘多项式的运算法则．
2．下列算式计算结果为x2﹣x﹣12的是（ ）
A．（x+3）（x﹣4）B．（x﹣3）（x+4）
C．（x﹣3）（x﹣4）D．（x+3）（x+4）
【考点】多项式乘多项式．
【专题】计算题．
【答案】A
【分析】利用十字相乘法分解因式即可得到结果．
【解答】解：x2﹣x﹣12＝（x+3）（x﹣4），
则（x+3）（x﹣4）＝x2﹣x﹣12．
故选：A．
【点评】此题考查了多项式乘多项式，熟练掌握十字相乘法是解本题的关键．
3．若（2x+m）（x﹣3）的展开式中不含x项，则实数m的值为（ ）
A．﹣6B．0C．3D．6
【考点】多项式乘多项式．
【专题】整式；运算能力．
【答案】D
【分析】先将式子进行展开，再合并同类项，然后根据题意进行求解即可．
【解答】解：∵（2x+m）（x﹣3）＝2x2﹣6x+mx﹣3m＝2x2+（m﹣6）x﹣3m，
又∵展开式中不含x项，
∴m﹣6＝0，
即m＝6，
故选：D．
【点评】本题考查多项式乘多项式的法则，不含某一项就是该项的系数等于0．先根据多项式乘多项式展开式子，合并同类项，不含x项，就是x项系数为0，进而求出m的值．
4．某同学在计算﹣3x加上一个多项式时错将加法做成了乘法，得到的答案是3x3﹣3x2+3x，由此可以推断出正确的计算结果是（ ）
A．﹣x2﹣2x﹣1B．x2+2x﹣1C．﹣x2+4x﹣1D．x2﹣4x+1
【考点】单项式乘多项式．
【专题】整式；运算能力．
【答案】A
【分析】先根据题意算出这个多项式，再与﹣3x相加即可．
【解答】解：由题意知，
这个多项式为x2+x﹣1，
∴正确的计算结果为﹣3x+（﹣x2+x﹣1）＝﹣x2﹣2x﹣1．
故选：A．
【点评】本题考查整式的混合运算，熟练掌握整式的混合运算的运算法则是解答本题的关键．
5．通过计算比较图1，图2中阴影部分的面积，可以验证的计算式子是（ ）
A．a（b﹣x）＝ab﹣ax
B．b（a﹣x）＝ab﹣bx
C．（a﹣x）（b﹣x）＝ab﹣ax﹣bx
D．（a﹣x）（b﹣x）＝ab﹣ax﹣bx+x2
【考点】多项式乘多项式；单项式乘多项式．
【答案】D
【分析】要求阴影部分面积，若不规则图形可考虑利用大图形的面积减去小图形的面积进行计算，若规则图形可以直接利用公式进行求解．
【解答】解：图1中，阴影部分＝长（a﹣x）宽（a﹣2b）长方形面积，
∴阴影部分的面积＝（a﹣x）（b﹣x），
图2中，阴影部分＝大长方形面积﹣长a宽x长方形面积﹣长b宽x长方形面积+边长x的正方形面积，
∴阴影部分的面积＝ab﹣ax﹣bx+x2，
∴（a﹣x）（b﹣x）＝ab﹣ax﹣bx+x2．
故选：D．
【点评】本题考查多项式乘多项式，单项式乘多项式，整式运算，需要利用图形的一些性质得出式子，考查学生观察图形的能力．
二．填空题（共5小题）
6．已知x+y＝3，xy＝1，则（x﹣2）（y﹣2）＝ ﹣1 ．
【考点】多项式乘多项式．
【专题】整式；运算能力．
【答案】见试题解答内容
【分析】把x+y＝3，xy＝1，代入（x﹣2）（y﹣2）＝xy﹣2（x+y）+4进行求解即可．
【解答】解：∵x+y＝3，xy＝1，
∴（x﹣2）（y﹣2）
＝xy﹣2x﹣2y+4
＝xy﹣2（x+y）+4
＝1﹣2×3+4
＝﹣1．
故答案为：﹣1．
【点评】本题主要考查多项式乘多项式，解题的关键是注意整体思想的应用．
7．若x﹣y＝3且xy＝1，则代数式（1+x）（y﹣1）的值等于 ﹣3 ．
【考点】多项式乘多项式．
【专题】整式；运算能力．
【答案】见试题解答内容
【分析】将原式化为xy﹣（x﹣y）﹣1，再代入计算即可．
【解答】解：∵x﹣y＝3，xy＝1，
∴（1+x）（y﹣1）
＝y﹣1+xy﹣x
＝xy﹣（x﹣y）﹣1
＝1﹣3﹣1
＝﹣3．
故答案为：﹣3．
【点评】本题考查多项式乘多项式，掌握多项式乘多项式的计算方法是正确解答的前提．
8．计算：2a2•（﹣3a）＝ ﹣6a3 ．
【考点】单项式乘单项式．
【专题】整式；运算能力．
【答案】﹣6a3．
【分析】先把系数相乘，然后利用同底数幂的乘法计算．
【解答】解：原式＝﹣6a3．
故答案为：﹣6a3．
【点评】本题考查了单项式乘单项式：单项式与单项式相乘，把他们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式．
9．计算：a2b•ab﹣1＝ a3 ．
【考点】单项式乘单项式；负整数指数幂．
【专题】整式；运算能力．
【答案】a3．
【分析】利用单项式乘单项式的法则进行运算即可．
【解答】解：a2b•ab﹣1＝a3．
故答案为：a3．
【点评】本题主要考查单项式乘单项式，解答的关键是对相应的运算法则的掌握．
10．对于实数a，b，c，d，规定一种运算ad﹣bc，如1×（﹣2）﹣0×2＝﹣2，那么当27时，则x＝ 22 ．
【考点】多项式乘多项式．
【专题】新定义．
【答案】见试题解答内容
【分析】由题中的新定义可知，此种运算为对角线乘积相减的运算，化简所求的式子得到关于x的方程，利用多项式乘多项式的运算法则及平方差公式化简合并即可求出x的值．
【解答】解：∵27，
∴（x+1）（x﹣1）﹣（x+2）（x﹣3）＝27，
∴x2﹣1﹣（x2﹣x﹣6）＝27，
∴x2﹣1﹣x2+x+6＝27，
∴x＝22；
故答案为：22．
【点评】此题考查学生理解新定义及灵活运用新定义的能力，同时也考查了学生会进行整式的混合运算及会利用平方差公式来化简运算，是一道中档题．
三．解答题（共5小题）
11．老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下：
×（xy）＝3x2y﹣xy2xy
（1）求所捂的多项式；
（2）若x，y，求所捂多项式的值．
【考点】单项式乘多项式．
【答案】见试题解答内容
【分析】（1）设多项式为A，则A＝（3x2y﹣xy2xy）÷（xy）计算即可．
（2）把x，y代入多项式求值即可．
【解答】解：（1）设多项式为A，
则A＝（3x2y﹣xy2xy）÷（xy）＝﹣6x+2y﹣1．
（2）∵x，y，
∴原式＝﹣621＝﹣4+1﹣1＝﹣4．
【点评】本题考查单项式乘多项式、多项式除以单项式的法则，解题的关键是利用乘法与除法是互为逆运算，把乘法转化为除法解决问题，属于基础题．
12．现有甲、乙、丙三种矩形卡片各若干张，卡片的边长如图所示（a＞1）．某同学分别用6张卡片拼出了两个矩形（不重叠无缝隙），如表2和表3，其面积分别为S1，S2．
表2
表3
（1）请用含a的式子分别表示S1，S2，当a＝2时，求S1+S2的值；
（2）比较S1与S2的大小，并说明理由．
【考点】多项式乘多项式．
【专题】数与式；运算能力．
【答案】（1）S1＝a2+3a+2，S2＝5a+1，当a＝2时，S1+S2＝23；
（2）S1＞S2，理由见解析．
【分析】（1）根据图形，利用长方形的面积公式计算即可；
（2）利用作差法比较即可．
【解答】解：（1）由图可知S1＝（a+2）（a+1）＝a2+3a+2，S2＝（5a+1）×1＝5a+1，
当a＝2时，S1+S2＝4+6+2+10+1＝23；
（2）S1＞S2，
理由：∵S1﹣S2＝a2+3a+2﹣5a﹣1＝a2﹣2a+1＝（a﹣1）2，
又∵a＞1，
∴（a﹣1）2＞0，
∴S1＞S2．
【点评】本题考查了多项式乘多项式，关键是能列出整式或算式表示几何图形的面积．
13．计算：xy4•（﹣x4﹣3）．
【考点】单项式乘多项式；幂的乘方与积的乘方；单项式乘单项式．
【专题】整式；运算能力．
【答案】﹣14x5y4+3xy4．
【分析】先根据幂的乘方与积的乘方运算法则计算，再合并同类项即可．
【解答】解：
3x•x4y4+x5y4+3xy4
＝﹣18x5y4+3x5y4+x5y4+3xy4
＝﹣14x5y4+3xy4．
【点评】本题主要考查整式的混合运算，解题关键是熟练掌握幂的乘方法则：底数不变，指数相乘[（am）n＝amn，m，n为正整数]．积的乘方法则：把每一个因式分别乘方，再把所得的幂相乘[（ab）n＝anbn，n为正整数]．
14．如图，有一块长为（3a+4b）米，宽为（2a+3b）米的长方形地，规划部门计划将阴影部分进行绿化，中间将建成一座边长为（a+b）米的正方形水池．
（1）用含有a，b的式子表示绿化部分面积；（结果要化简）
（2）若a＝5，b＝3，求出此时的绿化总面积．
【考点】多项式乘多项式；列代数式；代数式求值．
【专题】整式；运算能力．
【答案】（1）（5a2+15ab+11b2）平方米；
（2）449平方米．
【分析】（1）绿化部分的面积等于整体面积减去正方形水池面积；
（2）将a＝5，b＝3代入求解．
【解答】解：（1）长方形地块的面积＝（3a+4b）（2a+3b）
＝（6a2+17ab+12b2）平方米，
正方形的面积为：（a+b）2＝（a2+2ab+b2）平方米，
则绿化面积S＝（6a2+17ab+12b2）﹣（a2+2ab+b2）
＝（5a2+15ab+11b2）平方米；
（2）∵a＝5，b＝3，
∴绿化总面积S＝5a2+15ab+11b2
＝5×52+15×5×3+11×32
＝449（平方米）．
【点评】本题主要考查了整式的乘法运算的应用，熟练掌握运算法则和乘法公式是解答本题的关键．
15．计算：
（1）2a（a﹣3）﹣a2；
（2）（x﹣1）（x+2）﹣x（x+1）．
【考点】多项式乘多项式；单项式乘多项式．
【专题】整式；运算能力．
【答案】（1）a2﹣6a；
（2）﹣2．
【分析】（1）先根据单项式乘以多项式的运算法则进行计算，再合并同类项即可；
（2）先根据多项式乘多项式、单项式乘以多项式的乘法法则进行计算，再合并同类项即可．
【解答】解：（1）2a（a﹣3）﹣a2
＝2a2﹣6a﹣a2
＝a2﹣6a；
（2）（x﹣1）（x+2）﹣x（x+1）
＝x2+x﹣2﹣x2﹣x
＝﹣2．
【点评】本题考查整式的混合运算，熟练掌握单项式乘多项式、多项式乘多项式的乘法法则及合并同类项法则是解题的关键．
考点卡片
1．列代数式
（1）定义：把问题中与数量有关的词语，用含有数字、字母和运算符号的式子表示出来，就是列代数式．
（2）列代数式五点注意：①仔细辨别词义． 列代数式时，要先认真审题，抓住关键词语，仔细辩析词义．如“除”与“除以”，“平方的差（或平方差）”与“差的平方”的词义区分． ②分清数量关系．要正确列代数式，只有分清数量之间的关系． ③注意运算顺序．列代数式时，一般应在语言叙述的数量关系中，先读的先写，不同级运算的语言，且又要体现出先低级运算，要把代数式中代表低级运算的这部分括起来．④规范书写格式．列代数时要按要求规范地书写．像数字与字母、字母与字母相乘可省略乘号不写，数与数相乘必须写乘号；除法可写成分数形式，带分数与字母相乘需把代分数化为假分数，书写单位名称什么时不加括号，什么时要加括号．注意代数式括号的适当运用． ⑤正确进行代换．列代数式时，有时需将题中的字母代入公式，这就要求正确进行代换．
【规律方法】列代数式应该注意的四个问题
1．在同一个式子或具体问题中，每一个字母只能代表一个量．
2．要注意书写的规范性．用字母表示数以后，在含有字母与数字的乘法中，通常将“×”简写作“•”或者省略不写．
3．在数和表示数的字母乘积中，一般把数写在字母的前面，这个数若是带分数要把它化成假分数．
4．含有字母的除法，一般不用“÷”（除号），而是写成分数的形式．
2．代数式求值
（1）代数式的值：用数值代替代数式里的字母，计算后所得的结果叫做代数式的值．
（2）代数式的求值：求代数式的值可以直接代入、计算．如果给出的代数式可以化简，要先化简再求值．
题型简单总结以下三种：
①已知条件不化简，所给代数式化简；
②已知条件化简，所给代数式不化简；
③已知条件和所给代数式都要化简．
3．幂的乘方与积的乘方
（1）幂的乘方法则：底数不变，指数相乘．
（am）n＝amn（m，n是正整数）
注意：①幂的乘方的底数指的是幂的底数；②性质中“指数相乘”指的是幂的指数与乘方的指数相乘，这里注意与同底数幂的乘法中“指数相加”的区别．
（2）积的乘方法则：把每一个因式分别乘方，再把所得的幂相乘．
（ab）n＝anbn（n是正整数）
注意：①因式是三个或三个以上积的乘方，法则仍适用；②运用时数字因数的乘方应根据乘方的意义，计算出最后的结果．
4．单项式乘单项式
运算性质：单项式与单项式相乘，把他们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式．
注意：①在计算时，应先进行符号运算，积的系数等于各因式系数的积；②注意按顺序运算；③不要丢掉只在一个单项式里含有的字母因式；④此性质对于多个单项式相乘仍然成立．
5．单项式乘多项式
（1）单项式与多项式相乘的运算法则：单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加．
（2）单项式与多项式相乘时，应注意以下几个问题：
①单项式与多项式相乘实质上是转化为单项式乘以单项式；②用单项式去乘多项式中的每一项时，不能漏乘；③注意确定积的符号．
6．多项式乘多项式
（1）多项式与多项式相乘的法则：
多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．
（2）运用法则时应注意以下两点：
①相乘时，按一定的顺序进行，必须做到不重不漏；②多项式与多项式相乘，仍得多项式，在合并同类项之前，积的项数应等于原多项式的项数之积．
7．负整数指数幂
负整数指数幂：a﹣p（a≠0，p为正整数）
注意：①a≠0；
②计算负整数指数幂时，一定要根据负整数指数幂的意义计算，避免出现（﹣3）﹣2＝（﹣3）×（﹣2）的错误．
③当底数是分数时，只要把分子、分母颠倒，负指数就可变为正指数．
④在混合运算中，始终要注意运算的顺序．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2024/2/29 16:16:27；用户：组卷4；邮箱：zyb004@xyh.cm；学号：41418967

菁优网APP 菁优网公众号 菁优网小程序