2023—2024学年下学期初中数学沪教新版七年级期中必刷常考题之同位角、内错角、同旁内角

这是一份2023—2024学年下学期初中数学沪教新版七年级期中必刷常考题之同位角、内错角、同旁内角，共19页。试卷主要包含了如图所示，∠B与∠3是一对，如图，有下列判断，如图，给出以下结论等内容，欢迎下载使用。
1．下列图中∠1，∠2不是同位角的是（ ）
A．B．
C．D．
2．如图所示，∠B与∠3是一对（ ）
A．同位角B．内错角C．同旁内角D．对顶角
3．下列图中，∠1与∠2是同位角的是（ ）
A．B．
C．D．
4．如图，直线a，b被直线c所截，∠1与∠2是（ ）
A．同位角B．内错角C．同旁内角D．对顶角
二．填空题（共8小题）
5．如图，直线AB与直线CD交于点M，与直线EF交于点N，根据图形可知，∠ANF的内错角是 ．
6．如图，有下列判断：①∠A与∠1是同位角；②∠A与∠B是同旁内角；③∠4与∠1是内错角；④∠1与∠3是同位角．其中正确的是 （填序号）．
7．如图，∠B的内错角是 ；∠C的同旁内角是 ．
8．如图，给出以下结论：
①∠1与∠3是对顶角；
②∠1与∠3是同旁内角；
③∠2与∠5是同位角；
④∠3与∠4是内错角．
其中正确的是 ．（填序号）
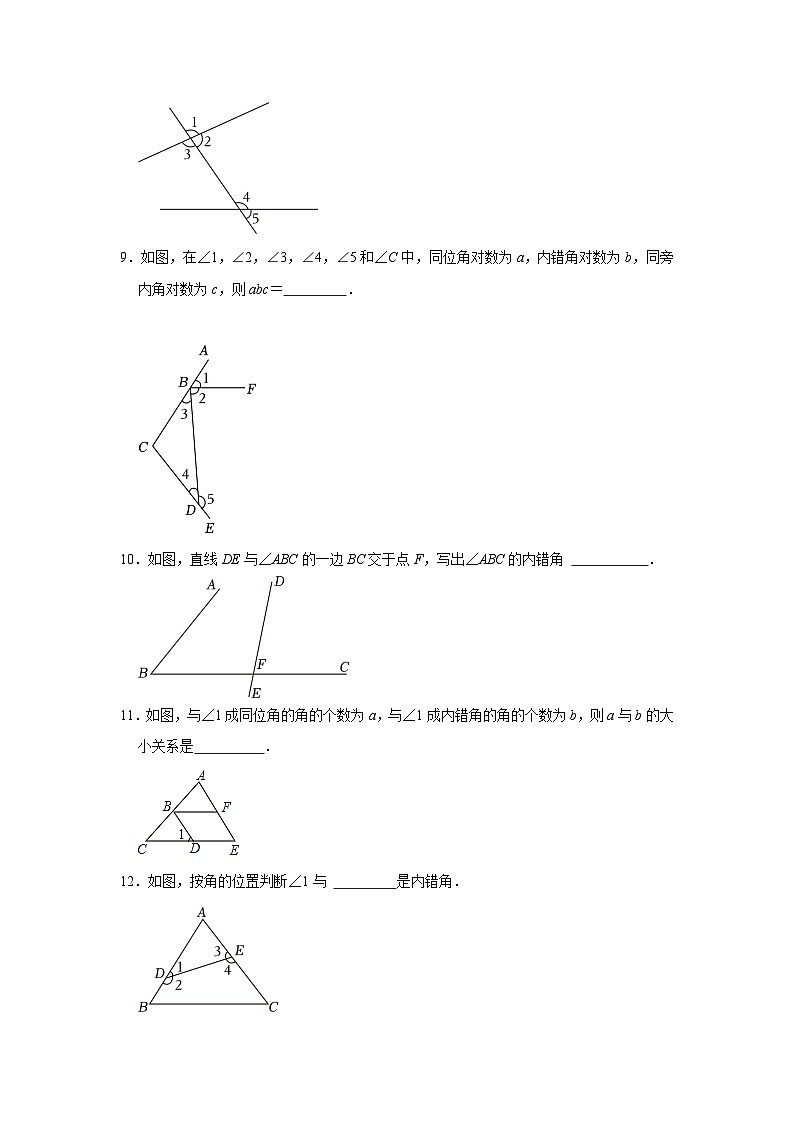
9．如图，在∠1，∠2，∠3，∠4，∠5和∠C中，同位角对数为a，内错角对数为b，同旁内角对数为c，则abc＝ ．
10．如图，直线DE与∠ABC的一边BC交于点F，写出∠ABC的内错角 ．
11．如图，与∠1成同位角的角的个数为a，与∠1成内错角的角的个数为b，则a与b的大小关系是 ．
12．如图，按角的位置判断∠1与 是内错角．
三．解答题（共3小题）
13．如图，已知直线EF与AB交于点M，与CD交于点O，OG平分∠DOF，若∠COM＝120°，∠EMB∠COF．
（1）求∠FOG的度数；
（2）写出一个与∠FOG互为同位角的角；
（3）求∠AMO的度数．
14．如图1，对于两条直线l1，l2被第三条直线l3所截的同旁内角∠α，∠β满足∠β＝∠α+30°，则称∠β是∠α的关联角．
（1）已知∠β是∠α的关联角．
①当∠α＝50°时，∠β＝ °；
②当2∠α﹣∠β＝45°时，直线l1，l2的位置关系为 ；
（2）如图2，已知∠AGH是∠CHG的关联角，点O是直线EF上一定点．
①求证：∠DHG是∠BGH的关联角；
②过点O的直线MN分别交直线CD，AB于点P，Q，且∠CHG＝80°．当∠EOP是图中某角的关联角时，写出所有符合条件的∠EOP的度数为 ．
15．如图所示，把一根筷子一端放在水里，一端露出水面，筷子变弯了，它真的弯了吗？其实没有，这是光的折射现象，光从空气中射入水中，光的传播方向发生了改变．
（1）请指出与∠1是同旁内角的有哪些角？请指出与∠2是内错角的有哪些角？
（2）若∠1＝115°，测得∠BOM＝145°，从水面上看斜插入水中的筷子，水下部分向上折弯了多少度？请说明理由．
2023—2024学年下学期初中数学沪教新版七年级期中必刷常考题之同位角、内错角、同旁内角
参考答案与试题解析
一．选择题（共4小题）
1．下列图中∠1，∠2不是同位角的是（ ）
A．B．
C．D．
【考点】同位角、内错角、同旁内角．
【专题】线段、角、相交线与平行线；几何直观．
【答案】D
【分析】根据同位角的定义（在被截线同一侧，截线的同一方位的两个角互为同位角）解决此题．
【解答】解：A．由图可知，∠1，∠2是同位角，故A不符合题意．
B．由图可知，∠1，∠2是同位角，故B不符合题意．
C．由图可知，∠1，∠2是同位角，故C不符合题意．
D．由图可知，∠1，∠2不是同位角，故D符合题意．
故选：D．
【点评】本题主要考查同位角，熟练掌握同位角的定义是解决本题的关键．
2．如图所示，∠B与∠3是一对（ ）
A．同位角B．内错角C．同旁内角D．对顶角
【考点】同位角、内错角、同旁内角；对顶角、邻补角．
【专题】线段、角、相交线与平行线；几何直观；应用意识．
【答案】C
【分析】根据“同位角、内错角、同旁内角”的意义进行判断即可．
【解答】解：∠B与∠3是直线DE和直线BC被直线AB所截得到的同旁内角，
故选：C．
【点评】本题考查“同位角、内错角、同旁内角”的意义，理解和掌握“同位角、内错角、同旁内角”的特征是正确判断的前提．
3．下列图中，∠1与∠2是同位角的是（ ）
A．B．
C．D．
【考点】同位角、内错角、同旁内角．
【专题】线段、角、相交线与平行线；几何直观．
【答案】B
【分析】根据同位角、内错角、同旁内角的定义判断即可．
【解答】解：选项A中的两个角是同旁内角，故此选项不符合题意；
选项B中的两个角符合同位角的意义，故此选项符合题意；
选项C中的两个角既不是同位角、也不是内错角、同旁内角，故此选项不符合题意；
选项D不是两条直线被一条直线所截出现的角，故此选项不符合题意．
故选：B．
【点评】本题考查了同位角、内错角、同旁内角，掌握同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形是解题的关键．
4．如图，直线a，b被直线c所截，∠1与∠2是（ ）
A．同位角B．内错角C．同旁内角D．对顶角
【考点】同位角、内错角、同旁内角；对顶角、邻补角．
【专题】线段、角、相交线与平行线；几何直观．
【答案】C
【分析】两条直线被第三条直线所截形成的角中，若两个角都在两直线之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角，由此即可判断．
【解答】解：直线a，b被直线c所截，∠1与∠2是同旁内角．
故选：C．
【点评】本题考查同旁内角，关键是掌握同旁内角的定义．
二．填空题（共8小题）
5．如图，直线AB与直线CD交于点M，与直线EF交于点N，根据图形可知，∠ANF的内错角是 ∠CMB ．
【考点】同位角、内错角、同旁内角．
【专题】线段、角、相交线与平行线；符号意识．
【答案】∠CMB．
【分析】内错角：两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角．
【解答】解：由内错角的定义可知，∠ANF的内错角是∠CMB，
故答案为：∠CMB．
【点评】本题考查了内错角的定义，熟练掌握知识点是解题的关键．
6．如图，有下列判断：①∠A与∠1是同位角；②∠A与∠B是同旁内角；③∠4与∠1是内错角；④∠1与∠3是同位角．其中正确的是 ①② （填序号）．
【考点】同位角、内错角、同旁内角．
【答案】见试题解答内容
【分析】根据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角作答．
【解答】解：①由同位角的概念得出：∠A与∠1是同位角；
②由同旁内角的概念得出：∠A与∠B是同旁内角；
③由内错角的概念得出：∠4与∠1不是内错角，错误；
④由内错角的概念得出：∠1与∠3是内错角，错误．
故正确的有2个，是①②．
故答案为：①②．
【点评】本题考查了同位角、内错角、同旁内角的概念．三线八角中的某两个角是不是同位角、内错角或同旁内角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F”形，内错角的边构成“Z”形，同旁内角的边构成“U”形．
7．如图，∠B的内错角是 ∠BAD ；∠C的同旁内角是 ∠DAC，∠B，∠BAC ．
【考点】同位角、内错角、同旁内角．
【专题】线段、角、相交线与平行线；几何直观．
【答案】∠BAD；∠DAC，∠B，∠BAC．
【分析】根据内错角和同旁内角的定义进行填空即可．
【解答】解：∠B的内错角是∠BAD，同旁内角是∠DAC，∠B，∠BAC，
故答案为：∠BAD；∠DAC，∠B，∠BAC．
【点评】本题考查了内错角、同旁内角．解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．
8．如图，给出以下结论：
①∠1与∠3是对顶角；
②∠1与∠3是同旁内角；
③∠2与∠5是同位角；
④∠3与∠4是内错角．
其中正确的是 ①③④ ．（填序号）
【考点】同位角、内错角、同旁内角；对顶角、邻补角．
【专题】线段、角、相交线与平行线；推理能力．
【答案】①③④．
【分析】根据对顶角，同位角，内错角，同旁内角的定义分析即可．
【解答】解：①∠1与∠3是对顶角，故①正确；
②∠1与∠3是对顶角，故②错误；
③∠2与∠5是同位角，故③正确；
④∠3与∠4是内错角，故④正确．
故答案为：①③④．
【点评】本题考查了对顶角，同位角，内错角，同旁内角的定义，正确理解定义是解答本题的关键．
9．如图，在∠1，∠2，∠3，∠4，∠5和∠C中，同位角对数为a，内错角对数为b，同旁内角对数为c，则abc＝ 16 ．
【考点】同位角、内错角、同旁内角．
【专题】线段、角、相交线与平行线；运算能力．
【答案】16．
【分析】根据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角，结合图形进行分析即可进行分析即可
【解答】解：同位角有：∠1与∠C，∠5与∠C，
内错角：∠2与∠4，∠3与∠5，
同旁内角：∠2与∠5，∠3与∠4，∠4与∠C，∠3与∠C，
∴a＝2，b＝2，c＝4，
∴abc＝2×2×4＝16，
故答案为：16．
【点评】此题主要考查了三线八角，关键是掌握同位角的边构成“F”形，内错角的边构成“Z”形，同旁内角的边构成“U”形．
10．如图，直线DE与∠ABC的一边BC交于点F，写出∠ABC的内错角 ∠BFE ．
【考点】同位角、内错角、同旁内角．
【专题】线段、角、相交线与平行线；几何直观．
【答案】∠BFE．
【分析】根据内错角的定义：两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角叫作内错角，即可得解．
【解答】解：∠ABC的内错角是∠BFE，
故答案为：∠BFE．
【点评】本题考查了内错角，熟记内错角的概念是解题关键．
11．如图，与∠1成同位角的角的个数为a，与∠1成内错角的角的个数为b，则a与b的大小关系是 a＜b ．
【考点】同位角、内错角、同旁内角．
【专题】线段、角、相交线与平行线；几何直观．
【答案】见试题解答内容
【分析】根据内错角和同位角定义进行分析即可．
【解答】解：与∠1成同位角的角是∠E，则a＝1，
与∠1成内错角的角是∠FBD和∠ABD，则b＝2，
故a＜b，
故答案为：a＜b．
【点评】此题主要考查了同位角和内错角，关键是掌握同位角的边构成“F”形，内错角的边构成“Z”形，同旁内角的边构成“U”形．
12．如图，按角的位置判断∠1与 ∠4 是内错角．
【考点】同位角、内错角、同旁内角．
【专题】线段、角、相交线与平行线；几何直观．
【答案】∠4．
【分析】根据内错角的定义判断求解．
【解答】解：∠1和∠4是AB，AC被DE所截形成的内错角，
故答案为：∠4．
【点评】本题考查了同位角、内错角，同旁内角的定义，正确识别各种角的关系是解题的关键．
三．解答题（共3小题）
13．如图，已知直线EF与AB交于点M，与CD交于点O，OG平分∠DOF，若∠COM＝120°，∠EMB∠COF．
（1）求∠FOG的度数；
（2）写出一个与∠FOG互为同位角的角；
（3）求∠AMO的度数．
【考点】同位角、内错角、同旁内角；角平分线的定义；对顶角、邻补角．
【答案】见试题解答内容
【分析】（1）根据对顶角相等可得∠DOF的度数，再根据角平分线的定义可求∠FOG的度数；
（2）根据同位角的定义可求与∠FOG互为同位角的角；
（3）根据邻补角的性质可求∠COF，再根据已知条件和对顶角相等可求∠AMO的度数．
【解答】解：（1）∵∠COM＝120°，
∴∠DOF＝120°，
∵OG平分∠DOF，
∴∠FOG＝60°；
（2）与∠FOG互为同位角的角是∠BMF；
（3）∵∠COM＝120°，
∴∠COF＝60°，
∵∠EMB∠COF，
∴∠EMB＝30°，
∴∠AMO＝30°．
【点评】本题考查了同位角的定义，角平分线定义，对顶角、邻补角定义的应用，能综合运用知识点进行推理和计算是解此题的关键．
14．如图1，对于两条直线l1，l2被第三条直线l3所截的同旁内角∠α，∠β满足∠β＝∠α+30°，则称∠β是∠α的关联角．
（1）已知∠β是∠α的关联角．
①当∠α＝50°时，∠β＝ 80 °；
②当2∠α﹣∠β＝45°时，直线l1，l2的位置关系为 平行 ；
（2）如图2，已知∠AGH是∠CHG的关联角，点O是直线EF上一定点．
①求证：∠DHG是∠BGH的关联角；
②过点O的直线MN分别交直线CD，AB于点P，Q，且∠CHG＝80°．当∠EOP是图中某角的关联角时，写出所有符合条件的∠EOP的度数为 140°、145°或155° ．
【考点】同位角、内错角、同旁内角；角的计算．
【专题】线段、角、相交线与平行线；运算能力；推理能力．
【答案】（1）①80，②平行；（2）①证明过程见解答，②140°、145°或155°．
【分析】（1）①根据关联角所满足的关系式∠β＝∠α+30°即可解答，
②解∠β＝∠α+30°与2∠α﹣∠β＝45°构成的方程组，根据∠α和∠β的关系来确定直线l1，l2的位置关系．
（2）①由∠AGH与∠BGH、∠CHG与∠DHG的互补关系，求出∠DHG与∠BGH之间的大小关系，进而命题得以证明．
②根据直线MN过点O的形式可分4种情况，每种情况均有2个角与∠EOP互为同旁内角，因此共有4种情况，分别解出∠EOP的度数即可．
【解答】解：（1）①∵∠β是∠α的关联角，∠α＝50°，
∴∠β＝∠α+30°＝50°+30°＝80°．
故答案为：80．
②由题意可得方程组，解得，
∴∠α+∠β＝75°+105°＝180°，
∴l1∥l2．
故答案为：平行．
（2）①证明：∵∠AGH是∠CHG的关联角，
∴∠AGH＝∠CHG+30°，
又∵∠DHG＝180°﹣∠CHG，∠BGH＝180°﹣∠AGH，
∴∠DHG﹣∠BGH＝180°﹣∠CHG﹣（180°﹣∠AGH）＝∠AGH﹣∠CHG＝30°，
∴∠DHG＝∠BGH+30°，
∴∠DHG是∠BGH的关联角．
②当直线MN位于如图所示位置时：
∵∠AGH是∠CHG的关联角，∠CHG＝80°，
∴∠AGH＝∠CHG+30°＝80°+30°＝110°．
若∠EOP是∠AGO的关联角，则∠EOP＝∠AGO+30°＝110°+30°＝140°．
若∠EOP是∠CPO的关联角，则∠EOP＝∠CPO+30°＝80°+180°﹣∠EOP+30°＝290°﹣∠EOP，得∠EOP＝145°．
当直线MN位于如图所示位置时：
∵∠AGH＝110°，∠CHG＝80°，
∴∠BGH＝180°﹣∠AGH＝180°﹣110°＝70°，∠GHD＝180°﹣∠CHG＝180°﹣80°＝100°
若∠EOP是∠BGO的关联角，则∠EOP＝∠BGO+30°＝70°+30°＝100°．
∵∠EOP＝∠GHD+∠OPH＝100°+∠OPH＞100°，
∴∠EOP＝100°（舍去）．
若∠EOP是∠DPO的关联角，则∠EOP＝∠DPO+30°＝100°+180°﹣∠EOP+30°＝310°﹣∠EOP，得∠EOP＝155°．
故答案为：140°、145°或155°．
【点评】本题考查了同旁内角及角的计算，难度不大，注意分情况讨论．
15．如图所示，把一根筷子一端放在水里，一端露出水面，筷子变弯了，它真的弯了吗？其实没有，这是光的折射现象，光从空气中射入水中，光的传播方向发生了改变．
（1）请指出与∠1是同旁内角的有哪些角？请指出与∠2是内错角的有哪些角？
（2）若∠1＝115°，测得∠BOM＝145°，从水面上看斜插入水中的筷子，水下部分向上折弯了多少度？请说明理由．
【考点】同位角、内错角、同旁内角．
【专题】几何图形．
【答案】见试题解答内容
【分析】（1）根据同旁内角、内错角的定义（两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角；处于两条直线之间，处于第三条直线两侧的两个角叫内错角）逐个判断即可．
（2）根据平行线的性质解答即可．
【解答】解：（1）与∠1是同旁内角的有∠AOE，∠MOE，∠ADE；
与∠2是内错角的有∠MOE，∠AOE；
（2）∵AB∥CD，
∴∠BOE＝∠1＝115°，
∵∠BOM＝145°，
∴∠MOE＝∠BOM﹣∠BOE＝145°﹣115°＝30°，
∴往上弯了30°．
【点评】本题考查了对同旁内角定义，内错角定义的应用，主要考查学生的理解能力，题目是一道比较好的题目，难度适中．
考点卡片
1．角平分线的定义
（1）角平分线的定义
从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线．
（2）性质：若OC是∠AOB的平分线
则∠AOC＝∠BOC∠AOB或∠AOB＝2∠AOC＝2∠BOC．
（3）平分角的方法有很多，如度量法、折叠法、尺规作图法等，要注意积累，多动手实践．
2．角的计算
（1）角的和差倍分
①∠AOB是∠AOC和∠BOC的和，记作：∠AOB＝∠AOC+∠BOC．∠AOC是∠AOB和∠BOC的差，记作：∠AOC＝∠AOB﹣∠BOC．②若射线OC是∠AOB的三等分线，则∠AOB＝3∠BOC或∠BOC∠AOB．
（2）度、分、秒的加减运算．在进行度分秒的加减时，要将度与度，分与分，秒与秒相加减，分秒相加，逢60要进位，相减时，要借1化60．
（3）度、分、秒的乘除运算．①乘法：度、分、秒分别相乘，结果逢60要进位．②除法：度、分、秒分别去除，把每一次的余数化作下一级单位进一步去除．
3．对顶角、邻补角
（1）对顶角：有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，互为对顶角．
（2）邻补角：只有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，互为邻补角．
（3）对顶角的性质：对顶角相等．
（4）邻补角的性质：邻补角互补，即和为180°．
（5）邻补角、对顶角成对出现，在相交直线中，一个角的邻补角有两个．邻补角、对顶角都是相对与两个角而言，是指的两个角的一种位置关系．它们都是在两直线相交的前提下形成的．
4．同位角、内错角、同旁内角
（1）同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．
（2）内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．
（3）同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角．
（4）三线八角中的某两个角是不是同位角、内错角或同旁内角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2024/3/1 12:12:13；用户：组卷5；邮箱：zyb005@xyh.cm；学号：41418968

菁优网APP 菁优网公众号 菁优网小程序