

所属成套资源:2023—2024学年下学期初中数学人教新版七年级期中必刷常考题
2023—2024学年下学期初中数学人教新版七年级期中必刷常考题之实数
展开
这是一份2023—2024学年下学期初中数学人教新版七年级期中必刷常考题之实数,共17页。试卷主要包含了在实数,的相反数是,比较两数的大小,比较大小等内容,欢迎下载使用。
1.a,b是有理数,它们在数轴上的对应点的位置如图所示,把a,﹣a,b,﹣b按照从小到大的顺序排列,正确的是( )
A.﹣b<﹣a<a<bB.﹣b<a<﹣a<bC.﹣a<﹣b<a<bD.﹣b<b<﹣a<a
2.在实数:3.14159,1.010010001…,4,π,中,无理数有( )
A.1个B.2个C.3个D.4个
3.如图,点A,C都是数轴上的点,AB=AC,则数轴上点C所表示的数为( )
A.B.C.D.
4.的相反数是( )
A.B.±C.﹣5D.5
5.已知实数a,b在数轴上的位置如图,下列结论错误的是( )
A.a<1<bB.1<﹣a<bC.1<a<bD.﹣b<a<﹣1
二.填空题(共5小题)
6.比较两数的大小:2 3.(填“<”或“>”)
7.比较大小: .
8.如图,在数轴上点A表示的实数是 .
9.实数1的相反数是 .
10.若ab,且a、b是两个连续的整数,则(﹣b)a的值为 .
三.解答题(共5小题)
11.已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分.
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
12.材料:∵4<6<9,∴,即23,∴的整数部分是2,小数部分为.
问题:已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分.
(1)求的小数部分;
(2)求3a﹣b+c的平方根.
13.计算:
(1)(﹣1)2023|﹣5|;
(2)()31.
14.阅读下面的文字,解答问题:
我们知道是无理数,无理数是无限不循环小数,因此不能将的小数部分全部写出来,于是小慧用1来表示的小数部分,你明白小慧的表示方法吗?
事实上,因为的整数部分是1,将一个数减去它的整数部分,差就是小数部分.
例如:∵,即23,
∴的整数部分为2,小数部分为 .
请解答:(1)的整数部分是 ,小数部分是 ;
(2)已知x是8的整数部分,y是8的小数部分,求x﹣y的值
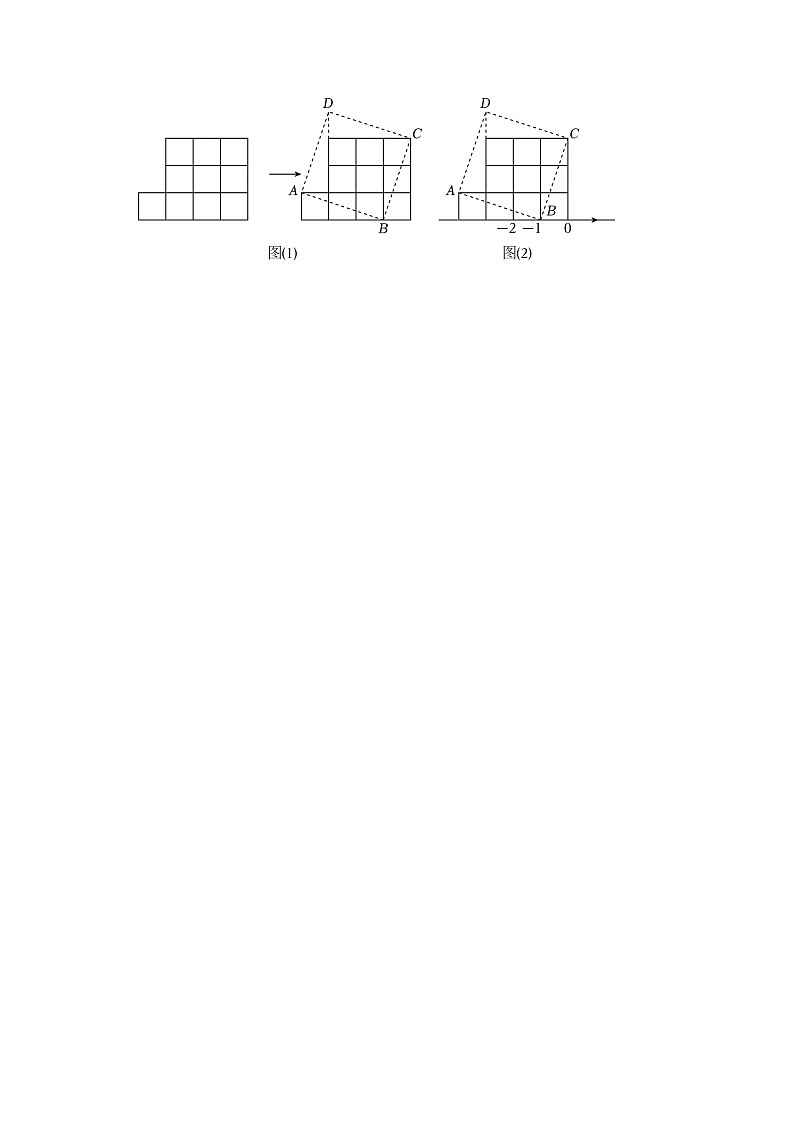
15.(图1)是由10个边长均为1的小正方形组成的图形,我们沿图的虚线AB,BC将它剪开后,重新拼成一个大正方形ABCD.
(1)在图(1)中,拼成的大正方形ABCD的面积为 ,边AD的长为 ;
知识运用:
(2)现将图(1)水平放置在如图(2)所示的数轴上,使得大正方形的顶点B与数轴上表示﹣1的点重合,若以点B为圆心,BC边的长为半径画圆,与数轴交于点E,求点E表示的数.
2023—2024学年下学期初中数学人教新版七年级期中必刷常考题之实数
参考答案与试题解析
一.选择题(共5小题)
1.a,b是有理数,它们在数轴上的对应点的位置如图所示,把a,﹣a,b,﹣b按照从小到大的顺序排列,正确的是( )
A.﹣b<﹣a<a<bB.﹣b<a<﹣a<bC.﹣a<﹣b<a<bD.﹣b<b<﹣a<a
【考点】实数大小比较;数轴.
【专题】实数;数感.
【答案】B
【分析】根据图示,可得:a<0<b,且﹣a<b,据此把a,﹣a,b,﹣b按照从小到大的顺序排列即可.
【解答】解:∵a<0<b,且﹣a<b,
∴﹣a>0,﹣b<0,
∵﹣a<b,
∴﹣b<a,
∴﹣b<a<﹣a<b.
故选:B.
【点评】此题主要考查了实数大小比较的方法,以及数轴的特征:一般来说,当数轴方向朝右时,右边的数总比左边的数大,要熟练掌握.
2.在实数:3.14159,1.010010001…,4,π,中,无理数有( )
A.1个B.2个C.3个D.4个
【考点】无理数.
【专题】实数;数感.
【答案】B
【分析】根据无理数的定义,即无限不循环小数或开方开不尽的数为无理数,即可解答.
【解答】解:在实数:3.14159,1.010010001…,4,π,中,无理数1.010010001…,π,共2个.、
∴排除A、C、D,
故选:B.
【点评】本题考查了无理数的定义,熟练掌握和运用无理数的定义是解决本题的关键.
3.如图,点A,C都是数轴上的点,AB=AC,则数轴上点C所表示的数为( )
A.B.C.D.
【考点】实数与数轴.
【专题】计算题;运算能力.
【答案】A
【分析】勾股定理得出AB,由AB=AC,即可得数轴上点C所表示的数.
【解答】解:A、B、﹣2处的点构成了直角三角形,
∴AB,
∵AB=AC,
∴AC,
∴C点所表示的数为1,
故选:A.
【点评】本题考查了勾股定理,注意观察A点的位置,得出数轴上点C所表示的数.
4.的相反数是( )
A.B.±C.﹣5D.5
【考点】实数的性质;平方根;算术平方根.
【专题】实数;数感.
【答案】A
【分析】根据相反数的意义求解即可.
【解答】解:的相反数是,
故选:A.
【点评】本题考查相反数,正确记忆在一个数的前面加上负号就是这个数的相反数是解题关键.
5.已知实数a,b在数轴上的位置如图,下列结论错误的是( )
A.a<1<bB.1<﹣a<bC.1<a<bD.﹣b<a<﹣1
【考点】实数与数轴.
【专题】实数;运算能力.
【答案】C
【分析】根据实数a,b在数轴上的位置结合绝对值表示该点到原点的距离即可得出答案.
【解答】解:根据实数a,b在数轴上的位置结合绝对值表示该点到原点的距离得出a<﹣1<0<1<b,且|a|<|b|,
即a<1<b,A选项正确,不符合题意,C选项错误,符合题意;
1<﹣a<b,B选项正确,不符合题意;
﹣b<a<﹣1,D选项正确,不符合题意.
故选:C.
【点评】本题主要考查了实数与数轴上的点一一对应的关系,熟练掌握正实数都大于0,负实数都小于0,正实数大于一切负实数是解题的关键.
二.填空题(共5小题)
6.比较两数的大小:2 > 3.(填“<”或“>”)
【考点】实数大小比较;算术平方根.
【专题】实数;推理能力.
【答案】见试题解答内容
【分析】首先分别求出两个实数的平方的值,比较出它们的大小关系;然后根据:两个正实数,平方大的,这个正实数也大,判断出2、3的大小关系即可.
【解答】解:12,32=9,
∵12>9,
∴23.
故答案为:>.
【点评】此题主要考查了实数大小比较的方法,解答此题的关键是要明确:正实数>0>负实数,两个正实数,平方大的,这个正实数也大.
7.比较大小: < .
【考点】实数大小比较.
【专题】实数;运算能力.
【答案】见试题解答内容
【分析】求出,根据5得出0,再得出答案即可.
【解答】解:
,
∵5,
∴0,
∴,
故答案为:<.
【点评】本题考查了估算无理数的范围和实数的大小比较,能选择适当的方法求解是解此题的关键.
8.如图,在数轴上点A表示的实数是 .
【考点】实数与数轴.
【专题】常规题型;数感.
【答案】
【分析】利用勾股定理求出三角形斜边长,再求出OA即可.
【解答】解:∵三角的直角边分别是1和2,
∴斜边长,
∴OA,
点A表示的实数是.
故答案为:.
【点评】本题考查李用数轴表示无理数的知识点,利用画弧的方法找点是解题关键.
9.实数1的相反数是 1 .
【考点】实数的性质.
【答案】见试题解答内容
【分析】根据只有符号不同的两个数互为相反数,可得答案.
【解答】解:1的相反数是1,
故答案为:1.
【点评】本题考查了实数的性质,在一个数的前面加上负号就是这个数的相反数.
10.若ab,且a、b是两个连续的整数,则(﹣b)a的值为 ﹣64 .
【考点】估算无理数的大小.
【专题】实数;二次根式;运算能力.
【答案】见试题解答内容
【分析】估算出的值,得到a,b的值,代入代数式计算即可.
【解答】解:∵9<13<16,
∴34,
∴a=3,b=4,
∴(﹣b)a=(﹣4)3=﹣64,
故答案为:﹣64.
【点评】本题考查了无理数的估算,无理数的估算常用夹逼法,用有理数夹逼无理数是解题的关键.
三.解答题(共5小题)
11.已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分.
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
【考点】估算无理数的大小.
【答案】见试题解答内容
【分析】(1)利用立方根的意义、算术平方根的意义、无理数的估算方法,求出a、b、c的值;
(2)将a、b、c的值代入代数式求出值后,进一步求得平方根即可.
【解答】解:(1)∵5a+2的立方根是3,3a+b﹣1的算术平方根是4,
∴5a+2=27,3a+b﹣1=16,
∴a=5,b=2,
∵c是的整数部分,
∴c=3.
(2)将a=5,b=2,c=3代入得:3a﹣b+c=16,
∴3a﹣b+c的平方根是±4.
【点评】此题考查立方根的意义、算术平方根的意义、无理数的估算方法、平方根的意义、代数式求值等知识点,读懂题意,掌握解答顺序,正确计算即可.
12.材料:∵4<6<9,∴,即23,∴的整数部分是2,小数部分为.
问题:已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分.
(1)求的小数部分;
(2)求3a﹣b+c的平方根.
【考点】估算无理数的大小;平方根.
【专题】实数;运算能力.
【答案】(1)3;(2)±4.
【分析】(1)估算出的范围,即可得到的小数部分;
(2)根据5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分求出a,b,c的值,然后求出3a﹣b+c的值,再求它的平方根.
【解答】解:(1)∵9<15<16,
∴34,
∴的整数部分是3,小数部分是3;
(2)∵5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分,
∴5a+2=33=27,3a+b﹣1=42=16,c=3,
∴a=5,b=2,c=3,
∴3a﹣b+c=15﹣2+3=16,
∴3a﹣b+c的平方根是±4.
【点评】本题考查了无理数的估算,立方根,平方根的定义,注意一个正数的平方根有两个,不要漏解.
13.计算:
(1)(﹣1)2023|﹣5|;
(2)()31.
【考点】实数的运算;绝对值;有理数的乘方;算术平方根;立方根.
【专题】实数;运算能力.
【答案】(1)0;
(2)0.875.
【分析】(1)利用有理数的乘方,算术平方根,绝对值的性质,立方根的定义进行计算即可;
(2)利用算术平方根的定义,算术平方根的定义进行计算即可.
【解答】解:(1)原式=﹣1+3﹣5﹣(﹣3)
=﹣1+3﹣5+3
=0;
(2)原式0.1251
=﹣0.5﹣0.125+2.5﹣1
=0.875.
【点评】本题考查实数的运算,熟练掌握相关运算法则是解题的关键.
14.阅读下面的文字,解答问题:
我们知道是无理数,无理数是无限不循环小数,因此不能将的小数部分全部写出来,于是小慧用1来表示的小数部分,你明白小慧的表示方法吗?
事实上,因为的整数部分是1,将一个数减去它的整数部分,差就是小数部分.
例如:∵,即23,
∴的整数部分为2,小数部分为 .
请解答:(1)的整数部分是 2 ,小数部分是 ;
(2)已知x是8的整数部分,y是8的小数部分,求x﹣y的值
【考点】估算无理数的大小.
【专题】实数;运算能力.
【答案】(1)2,;
(2).
【分析】(1)仿照题中给出的方法即可求出的整数部分和小数部分;
(2)先求出的取值范围即可求出的取值范围,从而得出其整数部分和小数部分,即可计算x﹣y的值.
【解答】解:(1)∵,
即,
∴的整数部分为2,小数部分为,
故答案为:2,;
(2)∵,
即,
∴,
∴的整数部分为11,小数部分为,
即x=11,y,
∴.
【点评】本题考查了无理数的估算,理解题意,熟练掌握无理数的估算方法是解题的关键.
15.(图1)是由10个边长均为1的小正方形组成的图形,我们沿图的虚线AB,BC将它剪开后,重新拼成一个大正方形ABCD.
(1)在图(1)中,拼成的大正方形ABCD的面积为 10 ,边AD的长为 ;
知识运用:
(2)现将图(1)水平放置在如图(2)所示的数轴上,使得大正方形的顶点B与数轴上表示﹣1的点重合,若以点B为圆心,BC边的长为半径画圆,与数轴交于点E,求点E表示的数.
【考点】实数与数轴.
【专题】实数;矩形 菱形 正方形;几何直观.
【答案】(1)大正方形ABCD的面积为10;AD;
(2)点E表示的数为﹣1或﹣1.
【分析】(1)根据10个边长均为1的小正方形剪开后,重新拼成一个大正方形ABCD可得正方形ABCD的面积,由正方形面积公式可得AD的长度;
(2)根据数轴上的点表示的数的特点可得E表示的数.
【解答】解:(1)∵由10个边长均为1的小正方形剪开后,重新拼成一个大正方形ABCD,
∴大正方形ABCD的面积为10×12=10;
∴AD2=10,
∴AD;
故答案为:10,;
(2)∵BC=AD,
∴以点B为圆心,BC边的长为半径画圆,与数轴交于点E,点E表示的数为﹣1或﹣1.
【点评】本题考查实数与数轴,解题的关键是掌握把无理数用数轴上的点表示.
考点卡片
1.数轴
(1)数轴的概念:规定了原点、正方向、单位长度的直线叫做数轴.
数轴的三要素:原点,单位长度,正方向.
(2)数轴上的点:所有的有理数都可以用数轴上的点表示,但数轴上的点不都表示有理数.(一般取右方向为正方向,数轴上的点对应任意实数,包括无理数.)
(3)用数轴比较大小:一般来说,当数轴方向朝右时,右边的数总比左边的数大.
2.绝对值
(1)概念:数轴上某个数与原点的距离叫做这个数的绝对值.
①互为相反数的两个数绝对值相等;
②绝对值等于一个正数的数有两个,绝对值等于0的数有一个,没有绝对值等于负数的数.
③有理数的绝对值都是非负数.
(2)如果用字母a表示有理数,则数a 绝对值要由字母a本身的取值来确定:
①当a是正有理数时,a的绝对值是它本身a;
②当a是负有理数时,a的绝对值是它的相反数﹣a;
③当a是零时,a的绝对值是零.
即|a|={a(a>0)0(a=0)﹣a(a<0)
3.有理数的乘方
(1)有理数乘方的定义:求n个相同因数积的运算,叫做乘方.
乘方的结果叫做幂,在an中,a叫做底数,n叫做指数.an读作a的n次方.(将an看作是a的n次方的结果时,也可以读作a的n次幂.)
(2)乘方的法则:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂都是0.
(3)方法指引:
①有理数的乘方运算与有理数的加减乘除运算一样,首先要确定幂的符号,然后再计算幂的绝对值;
②由于乘方运算比乘除运算又高一级,所以有加减乘除和乘方运算,应先算乘方,再做乘除,最后做加减.
4.平方根
(1)定义:如果一个数的平方等于a,这个数就叫做a的平方根,也叫做a的二次方根.
一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.
(2)求一个数a的平方根的运算,叫做开平方.
一个正数a的正的平方根表示为“”,负的平方根表示为“”.
正数a的正的平方根,叫做a的算术平方根,记作.零的算术平方根仍旧是零.
平方根和立方根的性质
1.平方根的性质:正数a有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
2.立方根的性质:一个数的立方根只有一个,正数的立方根是正数,负数的立方根是负数,0的立方根是0.
5.算术平方根
(1)算术平方根的概念:一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.记为.
(2)非负数a的算术平方根a有双重非负性:①被开方数a是非负数;②算术平方根a本身是非负数.
(3)求一个非负数的算术平方根与求一个数的平方互为逆运算,在求一个非负数的算术平方根时,可以借助乘方运算来寻找.
6.立方根
(1)定义:如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根.这就是说,如果x3=a,那么x叫做a的立方根.记作:.
(2)正数的立方根是正数,0的立方根是0,负数的立方根是负数.即任意数都有立方根.
(3)求一个数a的立方根的运算叫开立方,其中a叫做被开方数.
注意:符号中的根指数“3”不能省略;对于立方根,被开方数没有限制,正数、零、负数都有唯一一个立方根.
【规律方法】平方根和立方根的性质
1.平方根的性质:正数a有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
2.立方根的性质:一个数的立方根只有一个,正数的立方根是正数,负数的立方根是负数,0的立方根是0.
7.无理数
(1)、定义:无限不循环小数叫做无理数.
说明:无理数是实数中不能精确地表示为两个整数之比的数,即无限不循环小数.如圆周率、2的平方根等.
(2)、无理数与有理数的区别:
①把有理数和无理数都写成小数形式时,有理数能写成有限小数和无限循环小数,
比如4=4.0,0.33333…而无理数只能写成无限不循环小数,比如1.414213562.
②所有的有理数都可以写成两个整数之比;而无理数不能.
(3)学习要求:会判断无理数,了解它的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数,如分数是无理数,因为π是无理数.
无理数常见的三种类型
(1)开不尽的方根,如等.
(2)特定结构的无限不循环小数,
如0.303 003 000 300 003…(两个3之间依次多一个0).
(3)含有π的绝大部分数,如2π.
注意:判断一个数是否为无理数,不能只看形式,要看化简结果.如是有理数,而不是无理数.
8.实数的性质
(1)在实数范围内绝对值的概念与在有理数范围内一样.实数a的绝对值就是在数轴上这个数对应的点与原点的距离.
(2)实数的绝对值:正实数a的绝对值是它本身,负实数的绝对值是它的相反数,0的绝对值是0.
(3)实数a的绝对值可表示为|a|={a(a≥0)﹣a(a<0),就是说实数a的绝对值一定是一个非负数,即|a|≥0.并且有若|x|=a(a≥0),则x=±a.
实数的倒数
乘积为1的两个实数互为倒数,即若a与b互为倒数,则ab=1;反之,若ab=1,则a与b互为倒数,这里应特别注意的是0没有倒数.
9.实数与数轴
(1)实数与数轴上的点是一一对应关系.
任意一个实数都可以用数轴上的点表示;反之,数轴上的任意一个点都表示一个实数.数轴上的任一点表示的数,不是有理数,就是无理数.
(2)在数轴上,表示相反数的两个点在原点的两旁,并且两点到原点的距离相等,实数a的绝对值就是在数轴上这个数对应的点与原点的距离.
(3)利用数轴可以比较任意两个实数的大小,即在数轴上表示的两个实数,右边的总比左边的大,在原点左侧,绝对值大的反而小.
10.实数大小比较
实数大小比较
(1)任意两个实数都可以比较大小.正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数比大小,绝对值大的反而小.
(2)利用数轴也可以比较任意两个实数的大小,即在数轴上表示的两个实数,右边的总比左边的大,在原点左侧,绝对值大的反而小.
11.估算无理数的大小
估算无理数大小要用逼近法.
思维方法:用有理数逼近无理数,求无理数的近似值.
12.实数的运算
(1)实数的运算和在有理数范围内一样,值得一提的是,实数既可以进行加、减、乘、除、乘方运算,又可以进行开方运算,其中正实数可以开平方.
(2)在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.
另外,有理数的运算律在实数范围内仍然适用.
【规律方法】实数运算的“三个关键”
1.运算法则:乘方和开方运算、幂的运算、指数(特别是负整数指数,0指数)运算、根式运算、特殊三角函数值的计算以及绝对值的化简等.
2.运算顺序:先乘方,再乘除,后加减,有括号的先算括号里面的,在同一级运算中要从左到右依次运算,无论何种运算,都要注意先定符号后运算.
3.运算律的使用:使用运算律可以简化运算,提高运算速度和准确度.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2024/2/29 15:00:17;用户:组卷4;邮箱:zyb004@xyh.cm;学号:41418967
菁优网APP 菁优网公众号 菁优网小程序
相关试卷
这是一份2023—2024学年下学期初中数学人教新版期中必刷常考题之相交线,共19页。试卷主要包含了如图,下列结论正确的是等内容,欢迎下载使用。
这是一份2023—2024学年下学期初中数学人教新版七年级期中必刷常考题之平方根,共12页。试卷主要包含了4的算术平方根是,下列说法正确的是,81的算术平方根为,49的平方根是,若,则ab的值为,化简,有一个数值转换器,原理如图,的算术平方根是 等内容,欢迎下载使用。
这是一份2023—2024学年下学期初中数学人教新版七年级期中必刷常考题之立方根,共12页。试卷主要包含了下列说法不正确的是,下列选项中正确的是,下列各式中正确的是,下列各式正确的是,计算,﹣8的立方根是 ,的立方根是 等内容,欢迎下载使用。









