适用于新高考新教材备战2025届高考数学一轮总复习第6章数列第1节数列的概念与简单表示法课件新人教A版

这是一份适用于新高考新教材备战2025届高考数学一轮总复习第6章数列第1节数列的概念与简单表示法课件新人教A版，共44页。PPT课件主要包含了强基础固本增分，研考点精准突破，目录索引，数列的有关概念，确定的顺序，每一个数，数列的表示方法，Sn-Sn-1，数列的分类，常用结论等内容，欢迎下载使用。

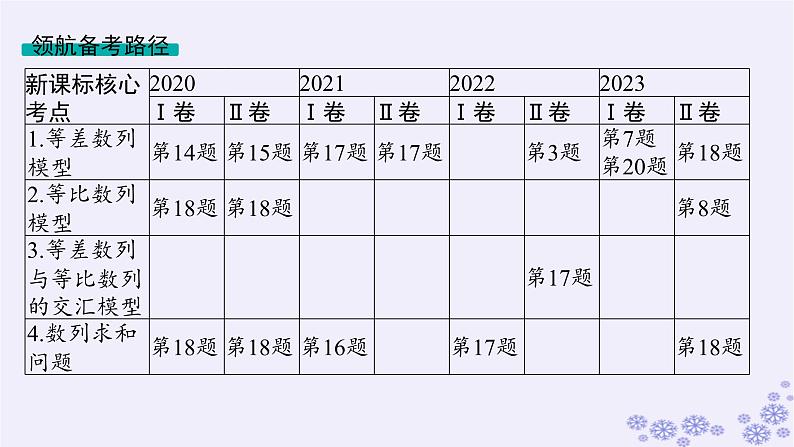
考情分析:从题型和题量上看,高考对本章考查多为“一大一小”的形式,有时也只考一道解答题.从内容上看,小题主要考查等差、等比数列基本量的运算,等差、等比数列的性质以及数列的递推关系等.解答题主要考查数列通项公式的求解、等差(等比)数列的判断与证明、数列求和等综合问题.
复习策略:1.熟记公式:要熟练记忆等差、等比数列的通项公式、前n项和公式、性质等,并要注意各个公式应用的条件.2.重视提高运算正确率:本单元中数学运算素养无处不在,需要加强训练,如乘公比错位相减法求和等,要掌握方法,规避易错点,不但要会做,还要做对.3.注重归纳规律:本章知识结构清晰,题型规律明显,要通过题目总结方法,并了然于胸,如什么情况下选择什么样的方法求数列的通项或前n项和,要对症下药,事半功倍.4.关注数学文化背景的数列试题:数列非常适宜与数学文化结合命题,尤其是中国古代数学名著中涉及的一些常见数列题,解决此类问题的关键是理解题意,转化为等差或等比数列等模型.
1.掌握数列的有关概念和表示方法.2.能利用an与Sn的关系以及递推关系求数列的通项公式.3.理解数列是一种特殊的函数,能利用数列的周期性、单调性解决简单的问题.
并非每一个数列都有通项公式,数列有通项公式时也不一定是唯一的
微点拨1.从函数观点看,数列{an}可以看成以正整数集N*(或它的有限子集)为定义域的函数an=f(n),当自变量按照从小到大的顺序依次取值时,所对应的一列函数值.2.对于一个数列,如果只知道它的前几项,而没有指出它的变化规律,是不能确定这个数列的.
微思考数列的通项公式an=3n+5与函数y=3x+5有何区别与联系?
提示 数列的通项公式an=3n+5是特殊的函数,其定义域为N*,而函数y=3x+5的定义域是R,an=3n+5的图象是离散的点,且排列在y=3x+5的图象上.
给出了数列相邻两项或多项之间的关系
数列的图象是坐标系中的一些孤立的点
3.an与Sn的关系
误区警示1.切记公式an=Sn-Sn-1成立的条件是n≥2,当n=1时,只能用a1=S1求解,根据Sn求an时一定要注意检验a1的值是否适合an=Sn-Sn-1.2.类比an与Sn的关系,若设数列{an}前n项的积为Tn(Tn≠0),则有
微思考数列的单调性与对应函数的单调性相同吗?
提示 不同.数列作为特殊的函数,也具有单调性,但其单调性与对应函数的单调性又有所不同,由于数列中项数n只能取正整数,所以当函数f(x)在[1,+∞)上单调时,数列{f(n)}也是单调数列,但当数列{f(n)}是单调数列时,函数f(x)不一定是单调函数,例如函数f(x)=(x- )2在[1,+∞)上不单调,但数列{an}(an=f(n))是递增数列.
题组一思考辨析(判断下列结论是否正确,正确的画“√”,错误的画“×”)1.根据数列的前几项归纳出数列的通项公式可能不止一个.(　　)2.1,1,1,1,…,不能构成一个数列.(　　)3.相同的一组数按不同顺序排列时都表示同一个数列.(　　)4.如果数列{an}的前n项和为Sn,则对∀n∈N*,都有an+1=Sn+1-Sn.(　　)
题组二回源教材5.(人教A版选择性必修第二册4.1节第8页练习第4题改编)已知数列{an}的前n项和公式为Sn=-2n2,则{an}的通项公式是　　　 　. 
6.(人教A版选择性必修第二册4.1节第8页练习第2(2)题改编)已知数列{an}满足a1=3,an= +1(n≥2),则a12=　　　　. 
解析 当n≥2时,an=Sn-Sn-1=-2n2-[-2(n-1)2]=-4n+2.当n =1时,a1=S1=-2,适合上式,故数列{an}的通项公式为an=-4n+2.
8.(2007·广东,文13)已知数列{an}的前n项和为Sn=n2-9n,则其通项公式an=　　　　;若它的第k项满足5解析 当n=1时,a1=1-9=-8,当n≥2时,an=Sn-Sn-1=n2-9n-[(n-1)2-9(n-1)]=2n-10,经检验当n=1时,也满足上式,因而an=2n-10.由5考点一 由an与Sn的关系求通项公式(多考向探究预测)
考向1已知Sn求an例1已知数列{an}的前n项和为Sn,且Sn=3n2+2n,则数列{an}的通项公式an=　　　　. 
解析 由题知Sn=3n2+2n,则Sn-1=3(n-1)2+2(n-1)=3n2-4n+1(n≥2),所以an=Sn-Sn-1=6n-1(n≥2).又a1=S1=5,符合上式,所以an=6n-1(n∈N*).
变式探究(变条件)本例中将“Sn=3n2+2n”改为“Sn=3n2+2n+1”,其余不变,则{an}的通项公式an=　　　　　　　. 
解析 由题知Sn=3n2+2n+1,则Sn-1=3(n-1)2+2(n-1)+1=3n2-4n+2(n≥2),所以an=Sn-Sn-1=6n-1(n≥2).又a1=S1=6,不符合上式.所以an=
[对点训练1](2024·四川成都模拟)已知数列{an}满足2a1+22a2+23a3+…+2nan=n·2n,则{an}的通项公式为(　　)
解析 当n=1时,有2a1=1·21,所以a1=1.由2a1+22a2+23a3+…+2nan=n·2n, 2a1+22a2+23a3+…+2n-1an-1=(n-1)·2n-1,n≥2,两式相减得2nan=n·2n-(n-1)2n-1
考向2已知Sn与an的关系式求an例2数列{an}的前n项和为Sn,若a1=1,an+1=5Sn(n≥1),则an=(　　)A.5×6nB.5×6n+1
变式探究(变条件)在本例中,若其他条件不变,将“an+1=5Sn(n≥1)”改为“an+1=5Sn+1(n≥1)”,再求an.
解 由已知an+1=5Sn+1(n≥1),得当n≥2时,an=5Sn-1+1,两式相减得an+1-an=5an,即an+1=6an,
因此数列{an}是首项为1,公比为6的等比数列,因此其通项公式为an=6n-1.
考点二 由数列的递推关系求通项公式(多考向探究预测)
例3(1)在数列{an}中,a1=2,an+1=an+ln(1+ ),则an等于(　　) A.2+ln nB.2+(n-1)ln nC.2+nln nD.1+n+ln n
解析 因为an+1-an= =ln(n+1)-ln n,所以a2-a1=ln 2-ln 1,a3-a2=ln 3-ln 2,a4-a3=ln 4-ln 3,…,an-an-1=ln n-ln(n-1)(n≥2).把以上各式分别相加得an-a1=ln n-ln 1,则an=2+ln n,n≥2.又a1=2也符合上式,因此an=2+ln n.
(2)已知在数列{an}中,a1=1, =n+1,则数列{an}的通项公式an=　　　　. 
考向2累乘法例4(2024·辽宁葫芦岛模拟)在数列{an}中,a1=4,nan+1=(n+2)an,则数列{an}的通项公式为an=　　 　　. 
[对点训练2](1)数列{an}的前五项分别是下列各数:1,3,6,10,15,则{an}的一个通项公式为(　　)
解析 依题意a2-a1=3-1=2,a3-a2=6-3=3,a4-a3=10-6=4,a5-a4=15-10=5,
(2)已知数列{an}的前n项和为Sn,且满足Sn=(n+1)2an-3,则{an}的通项公式为　　　　　　　. 
考点三 数列的性质(多考向探究预测)
[对点训练3]斐波那契数列因以兔子繁殖为例子而引入,故又称为“兔子数列”.此数列在现代物理、准晶体结构、化学等领域都有着广泛的应用.斐波那契数列{an}可以用如下方法定义:an+2=an+1+an,且a1=a2=1,若此数列各项除以4的余数依次构成一个新数列{bn},则数列{bn}的前2 022项和为(　　)A.2 698B.2 697C.2 696D.2 695
解析 ∵an=an-1+an-2(n≥3,n∈N*),a1=a2=1,∴数列{an}为1,1,2,3,5,8,13,21,34,55,89,144,…,此数列各项除以4的余数依次构成的数列{bn}为1,1,2,3,1,0,1,1,2,3,1,0,…,所以数列{bn}是以6为周期的周期数列,
考向2数列的单调性例6(2024·北京怀柔模拟)数列{an}的通项公式为an=(n-λ)·2n(n=1,2,…),若{an}是递增数列,则λ的取值范围是(　　)A.[1,+∞)B.(1+lg2e,3)C.(-∞,1+lg2e]D.(-∞,3)
解析 因为数列{an}的通项公式为an=(n-λ)·2n(n=1,2,…),且{an}是递增数列,所以an规律方法解决数列的单调性问题的3种方法
考向3数列的最值例7在数列{an}中,an=(2n-1)( )n,则数列{an}中的最大项是第　　　项.