初中4 二次函数y=ax2+bx+c的图象和性质备课课件ppt

这是一份初中4 二次函数y=ax2+bx+c的图象和性质备课课件ppt，文件包含34二次函数yax2+bx+c的图象与性质3ppt、34二次函数yax2+bx+c的图象与性质3doc等2份课件配套教学资源，其中PPT共15页， 欢迎下载使用。

如图所示是桥梁的两条钢缆具有相同的抛物线形状．按图中建立直角坐标系，右面的一条抛物线可以用y=0.0225x2-0.9x+10表示，而且左右两条抛物线关于y轴对称，请你写出左面钢缆的表达式
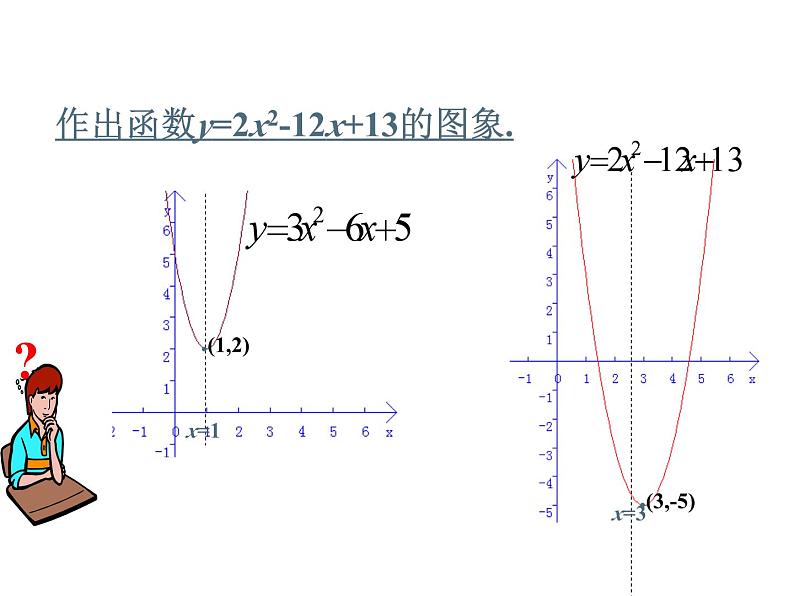
怎样直接作出函数y=3x2-6x+5的图象?
函数y=ax²+bx+c的图象
我们知道,作出二次函数y=3x2的图象,通过平移抛物线y=3x2可以得到二次函数y=3x2-6x+5的图象.
配方:加上再减去一次项系数绝对值一半的平方
整理:前三项化为平方形式,后两项合并同类项
老师提示:配方后的表达式通常称为配方式或顶点式
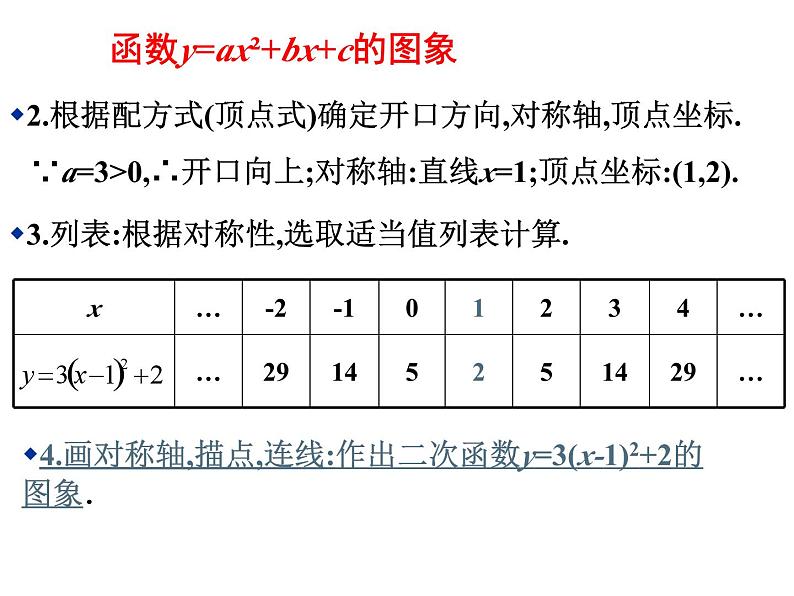
4.画对称轴,描点,连线:作出二次函数y=3(x-1)2+2的图象．
2.根据配方式(顶点式)确定开口方向,对称轴,顶点坐标.
3.列表:根据对称性,选取适当值列表计算.
∵a=3>0,∴开口向上;对称轴:直线x=1;顶点坐标:(1,2).
作出函数y=2x2-12x+13的图象.
例.求次函数y=ax²+bx+c的对称轴和顶点坐标．
函数y=ax²+bx+c的顶点式
一般地,对于二次函数y=ax²+bx+c,我们可以利用配方法推导出它的对称轴和顶点坐标.
老师提示:这个结果通常称为求顶点坐标公式.
因此,二次函数y=ax²+bx+c的图象是一条抛物线.
根据公式确定下列二次函数图象的对称轴和顶点坐标：
如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x²+0.9x+10表示,而且左右两条抛物线关手y轴对称．
⑴钢缆的最低点到桥面的距离是少？⑵两条钢缆最低点之间的距离是多少？⑶你是怎样计算的？与同伴交流.
⑴钢缆的最低点到桥面的距离是少？你是怎样计算的？与同伴交流.
可以将函数y=0.0225x2+0.9x+10配方,求得顶点坐标,从而获得钢缆的最低点到桥面的距离;
⑵两条钢缆最低点之间的距离是多少？你是怎样计算的？与同伴交流.
想一想,你知道图中右面钢缆的表达式是什么吗?
⑶你还有其它方法吗？与同伴交流.
直接利用顶点坐标公式再计算一下上面问题中钢缆的最低点到桥面的距离以及两条钢缆最低点之间的距离．
1.相同点: (1)形状相同(图像都是抛物线,开口方向相同). (2)都是轴对称图形. (3)都有最(大或小)值.(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 .
函数y=ax2+bx+c(a≠0)与y=ax²的关系
2.不同点: (1)位置不同(2)顶点不同:分别是 和(0,0). (3)对称轴不同:分别是 和y轴. (4)最值不同:分别是 和0.3.联系: y=a(x-h)²+k(a≠0) 的图象可以看成y=ax²的图象先沿x轴整体左(右)平移| |个单位(当 >0时,向右平移;当 <0时,向左平移),再沿对称轴整体上(下)平移| |个单位 (当 >0时向上平移;当 <0时,向下平移)得到的.
二次函数y=ax2+bx+c(a≠0)的图象和性质
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.