2023-2024学年黑龙江省双鸭山市集贤县八年级（上）期末数学试卷（含详细答案解析）

这是一份2023-2024学年黑龙江省双鸭山市集贤县八年级（上）期末数学试卷（含详细答案解析），共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
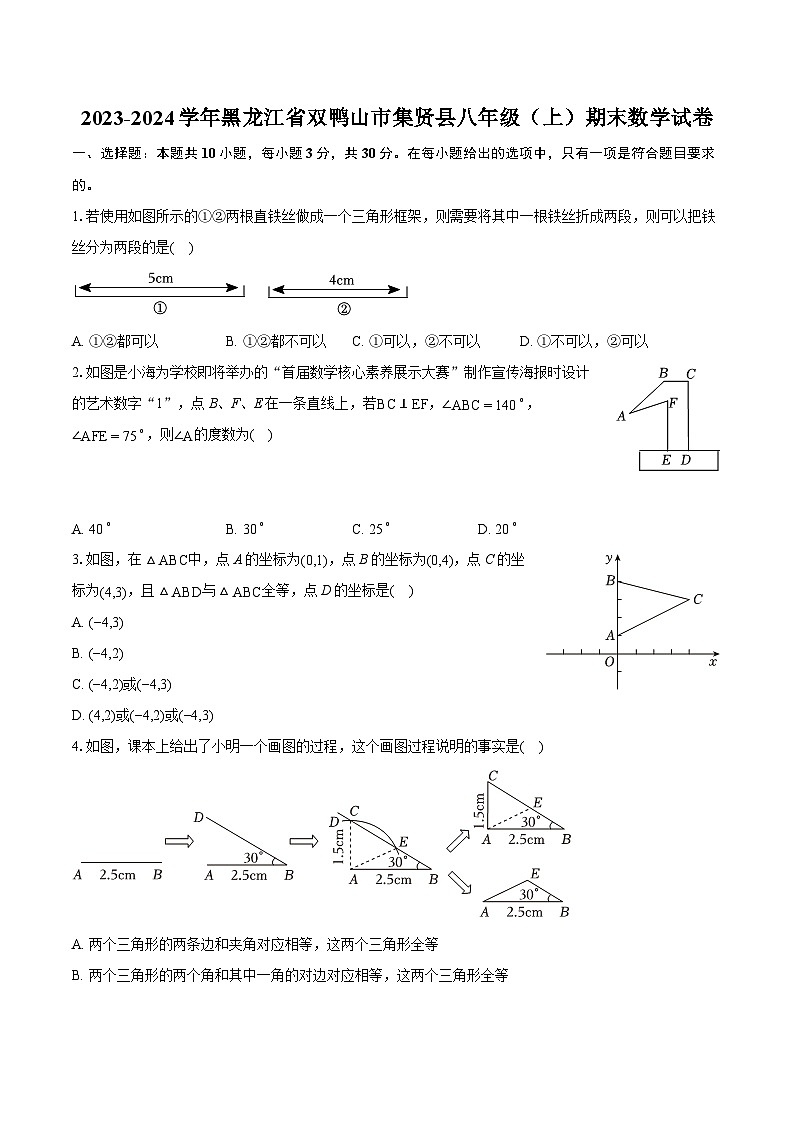
1.若使用如图所示的①②两根直铁丝做成一个三角形框架，则需要将其中一根铁丝折成两段，则可以把铁丝分为两段的是( )
A. ①②都可以B. ①②都不可以C. ①可以，②不可以D. ①不可以，②可以
2.如图是小海为学校即将举办的“首届数学核心素养展示大赛”制作宣传海报时设计的艺术数字“1”，点B、F、E在一条直线上，若BC⊥EF，∠ABC=140∘，∠AFE=75∘，则∠A的度数为( )
A. 40∘B. 30∘C. 25∘D. 20∘
3.如图，在△ABC中，点A的坐标为(0,1)，点B的坐标为(0,4)，点C的坐标为(4,3)，且△ABD与△ABC全等，点D的坐标是( )
A. (−4,3)
B. (−4,2)
C. (−4,2)或(−4,3)
D. (4,2)或(−4,2)或(−4,3)
4.如图，课本上给出了小明一个画图的过程，这个画图过程说明的事实是( )
A. 两个三角形的两条边和夹角对应相等，这两个三角形全等
B. 两个三角形的两个角和其中一角的对边对应相等，这两个三角形全等
C. 两个三角形的两条边和其中一边对角对应相等，这两个三角形不一定全等
D. 两个三角形的两个角和夹边对应相等，这两个三角形不一定全等
5.定义：两点关于某条直线对称，则称这条直线为这两个点的“幸福直线”.若点A(1,2)，幸福直线是x=−2，则点A关于这条幸福直线的对称点B的坐标，是( )
A. (−5,2)B. (−1,2)C. (1,−2)D. (−1,−2)
6.如图，在等腰三角形△ABC中，AB=AC，D为BC延长线上一点，EC⊥AC且AC=CE，垂足为C，连接BE，若BC=6，则△BCE的面积为( )
A. 92
B. 9
C. 18
D. 36
7.如图，美美不小心在课后作业的第1题滴了一点墨水，留下一道残缺不全的题目，则被墨水覆盖的部分为( )
A. x3−x2+xB. −x3−x2+xC. −x3+x2−xD. x3+x2−x
8.使分式aa+2有意义的a的取值范围是( )
A. a≥−2B. a=−2C. a≠−2D. a≤−2
9.下列多项式因式分解：
①x2−6xy+9y2=(x−3y)2；②16+a4=(4+a2)(4−a2)；③25ab2+10ab+5b=5b(5ab−2a)；④x2−(2y)2=(x−2y)(x+2y)，其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
10.如图，S1、S2分别表示边长为x、y的正方形的面积，且A、B、C三点在一条直线上，若S1+S2=20，AB=x+y=6，则图中阴影部分的面积为( )
A. 16
B. 12
C. 8
D. 4
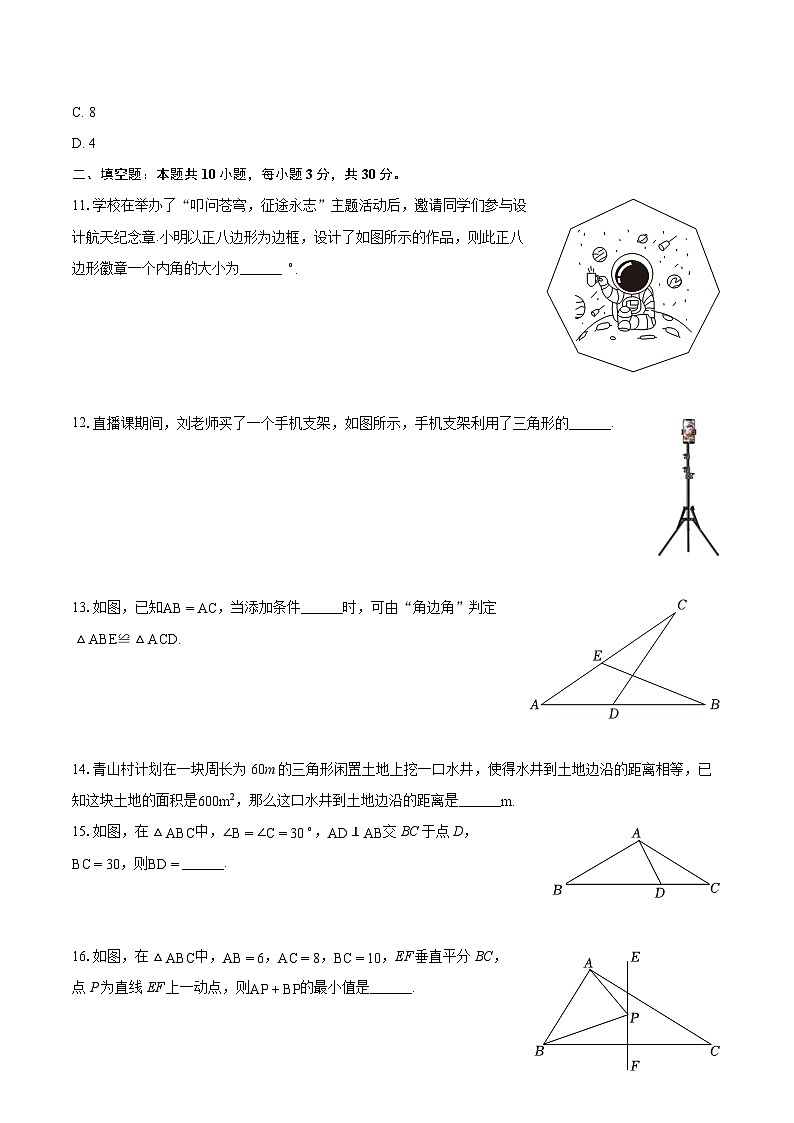
二、填空题：本题共10小题，每小题3分，共30分。
11.学校在举办了“叩问苍穹，征途永志”主题活动后，邀请同学们参与设计航天纪念章.小明以正八边形为边框，设计了如图所示的作品，则此正八边形徽章一个内角的大小为______ ∘.
12.直播课期间，刘老师买了一个手机支架，如图所示，手机支架利用了三角形的______.
13.如图，已知AB=AC，当添加条件______时，可由“角边角”判定△ABE≌△ACD.
14.青山村计划在一块周长为60m的三角形闲置土地上挖一口水井，使得水井到土地边沿的距离相等，已知这块土地的面积是600m2，那么这口水井到土地边沿的距离是______m.
15.如图，在△ABC中，∠B=∠C=30∘，AD⊥AB交BC于点D，BC=30，则BD=______.
16.如图，在△ABC中，AB=6，AC=8，BC=10，EF垂直平分BC，点P为直线EF上一动点，则AP+BP的最小值是______.
17.若a=2023，b=2022，则计算12a2−12b2的结果为______.
18.若分式x2−1x+1的值为0，则x应满足的条件是______.
19.分式方程axx−1+31−x=2无解，则a的值是______.
20.每立方厘米的空气质量约为0.0014g，用科学记数法表示为______g.
三、解答题：本题共8小题，共60分。解答应写出文字说明，证明过程或演算步骤。
21.(本小题5分)
计算：a5⋅(−a)3+a10÷a2+(−2a4)2.
22.(本小题5分)
分解因式：x4(m−2)+(2−m)y4.
23.(本小题6分)
先化简，再求值：a2−4a+4a2−4÷a−2a2+2a+3，其中a=(1− 3)0.
24.(本小题8分)
【例题讲解】仔细阅读下面的例题，解答问题：
例：已知二次三项式x2−4x+m有一个因式是(x+3)，求另一个因式以及m的值.
解：设另一个因式为(x+n)，得x2−4x+m=(x+3)(x+n)，
则x2−4x+m=x2+(n+3)x+3n，
∴n+3=−4m=3n
解得n=−7m=−21，
∴另一个因式为(x−7)，m的值为−21.
【方法归纳】
设某一多项式的全部或部分系数为未知数，利用当两个多项式为恒等式时，同类项系数相等的原理确定这些系数，从而得到待求的值，这种方法叫待定系数法.
【学以致用】
(1)若x2−mx−12=(x+3)(x−4)，则m=______；
(2)已知二次三项式2x2−5x+k有一个因式是2x−3，求另一个因式以及k的值；
(3)若多项式x2−mx+n(m、n是常数)分解因式后，有一个因式是x−2，则代数式9m3n的值.
25.(本小题7分)
如图.已知角△ABC，∠B=48∘，请用尺规作图法，在△ABC内部求作一点P.使PB=PC.且∠PBC=24∘.(保留作图痕迹，不写作法)
26.(本小题8分)
如图，在△ABC中，∠B=50∘，∠C=20∘.过点A作AE⊥BC，垂足为E，延长EA至点D.使AD=AC.在边AC上截取AF=AB，连接DF.求证：DF=CB.
27.(本小题11分)
为加快公共领域充电基础设施建设，某停车场计划购买A，B两种型号的充电桩.已知A型充电桩比B型充电桩的单价少0.3万元，且用12万元购买A型充电桩与用18万元购买B型充电桩的数量相等.
(1)A，B两种型号充电桩的单价各是多少？
(2)该停车场计划共购买20个A，B型充电桩，购买总费用不超过15万元，且A型充电桩购买数量不超过12个.问：共有哪几种购买方案？哪种方案所需购买总费用最少？
28.(本小题10分)
△ABC中，∠ACB=90∘，AC=BC，点D在射线BC上(不与B，C重合)，连接AD，过点B作BF⊥AD，垂足为F.
(1)如图1，点D在线段BC上，若AF恰好平分∠CAB，探究AC、CD、AB之间的数量关系，并说明理由.
(2)如图2，点D在线段BC上，点M是直线BF上的一点，且AF平分∠MAC，探究AC、CD、AM之间的数量关系，并说明理由.
(3)若点D在线段BC的延长线上(CD4，满足两边之和大于第三边．
故选：C.
三角形两边之和大于第三边．依此即可求解．
本题考查了三角形的三边关系，关键掌握三角形两边之和大于第三边，两边之差小于第三边．
2.【答案】C
【解析】解：延长EF交BC于点H，过点B作BT⊥BC交AF于点T，如图所示：
∵BT⊥BC
∴∠TBC=90∘，
∵∠ABC=140∘，
∴∠ABT=∠ABC−∠TBH=140∘−90∘=50∘，
∵∠AFE=75∘，
∴∠AFH=180∘−∠AFE=180∘−75∘=105∘，
∵BC⊥EF，BT⊥BC
∴BT//EF，
∴∠ATB=∠AFH=105∘，
∵∠A+∠ABT+∠ATB=180∘，
∴∠A=180∘−(∠ABT+∠ATB)=180∘−(50∘+105∘)=25∘.
故选：C.
延长EF交BC于点H，过点B作BT⊥BC交AF于点T，根据∠ABC=140∘可求出∠ABT=50∘，根据∠AFE=75∘可求出∠AFH=105∘，再证BT//EF得∠ATB=∠AFH=105∘，然后利用三角形的内角和定理可求出∠A的度数．
此题主要考查了三角形的内角和定理，平行线的性质，解答此题的关键是熟练掌握三角形的内角和等于180∘，两直线平行同位角相等；垂直于通一条直线的两条直线平行．
3.【答案】D
【解析】解：当△ABD1≌△ABC时，△ABD和△ABC关于y轴对称，如下图所示：
∴点D1的坐标是(−4,3)，
当△ABD2≌△BAC，过D2作D2G⊥AB，过C点作CH⊥AB，如上图所示，
△ABD2边AB上的高D2G与△BAC的边AB上高CH相等，
∴D2G=CH=4，AG=BH=1，
∴OG=2，
∴点D2的坐标是(−4,2)，
当△ABD3≌△BAC过D3作D3G⊥AB，如上图所示，
△ABD3边AB上的高D3G与△BAC的边AB上高CH相等，
∴D3G=CH=4，AG=BH=1，
∴OG=2，
∴点D3的坐标是(4,2)，
综上所述，点D的坐标是D1(−4,3)，D2(−4,2)或D3(4,2)，
故选：D.
利用对称的性质，当D点与C点关于y轴对称时，△ABD与△ABC全等；当点D与点C关于AB的垂直平分线对称时，△ABD与△ABC全等；点D点与(4,2)关于y轴对称时，△ABD与△ABC全等，然后写出对应D点坐标即可．
本题考查了全等三角形的性质，直角坐标系中的轴对称问题，根据对称性分情况讨论即可，掌握数形结合的思路是解题的关键．
4.【答案】C
【解析】解：根据作图可知：两个三角形的两条边和其中一边对角对应相等，其中角的对边不确定，可能有两种情况，故三角形不能确定，
所以两个三角形的两条边和其中一边对角对应相等，这两个三角形不一定全等，
故选：C.
根据全等三角形的判定进行判断即可．
本题考查了全等三角形的判定，熟知三角形全等的判定是解题的关键．
5.【答案】A
【解析】解：由题意知，B(−2×2−1,2)，即B(−5,2)，
故选：A.
由点A关于幸福直线x=−2的对称点B的坐标，可知A、B的纵坐标相同，横坐标和的一半等于−2，即B(−2×2−1,2)，然后作答即可．
本题考查了关于直线对称的点坐标的特征．熟练掌握关于直线对称的点坐标的特征是解题的关键．
6.【答案】B
【解析】解：过A作AH⊥BC于H，过E作EF⊥BC于F，
∵AB=AC，
∴BH=HC，
∵∠ACE=90∘，
∴∠ACH+∠ECF=90∘，
∵∠CAH+∠ACH=90∘，
∴∠ECF=∠CAH，
在△ACH与△CEF中，
∠AHC=∠CFE=90∘∠CAH=∠ECFAC=CE，
∴△ACH≌△CEF(AAS)，
∴EF=CH=12BC=3，
∴△BCE的面积=12BC⋅EF=12×6×3=9，
故选：B.
过A作AH⊥BC于H，过E作EF⊥BC于F，利用等腰三角形的性质和全等三角形的判定和性质解答即可．
此题考查全等三角形的判定和性质，关键是利用等腰三角形的性质和全等三角形的判定和性质解答．
7.【答案】B
【解析】解：被覆盖部分为(x2+x−1)(−x)=−x3−x2+x.
故选：B.
根据乘法和除法互为逆运算可知：被除式=商×除式，由此可求出被覆盖的部分．
本题考查了整式的乘法，熟练掌握整式的乘法是解题的关键．
8.【答案】C
【解析】解：由题意得，a+2≠0，
解得：a≠−2，
故选：C.
根据分式的分母不等于0列式计算即可得解．
本题考查了分式有意义的条件，解题的关键是根据分母不等于0列式计算．
9.【答案】B
【解析】解：①x2−6xy+9y2=(x−3y)2是正确的；
②16+a4不能因式分解，故原来的因式分解错误；
③25ab2+10ab+5b=5b(5ab+2a+1)，故原来的因式分解错误；
④x2−(2y)2=(x−2y)(x+2y)是正确的；
故其中正确的有2个．
故选：B.
利用提公因式法，公式法逐项进行因式分解即可．
本题考查因式分解，掌握提公因式法、公式法是正确判断的关键．
10.【答案】C
【解析】解：∵S1+S2=20，
∴x2+y2=20，
∵x+y=6，
∴(x+y)2=62，
∴x2+y2+2xy=36，
∴xy=8，
∵△BCD的面积=12BC⋅CD=12xy，△ACF的面积=12AC⋅CF=12xy，
∴阴影部分的面积=△BCD的面积+△ACF的面积=xy=8.
故选：C.
由正方形面积公式得到x2+y2=20，由完全平方公式求出xy=8，由三角形面积公式即可求出阴影的面积．
本题考查三角形的面积，正方形的面积，完全平方公式，关键是由完全平方公式得到xy=8.
11.【答案】135
【解析】解：(8−2)×180∘8=135∘，
即此正八边形徽章一个内角的大小为135∘，
故答案为：135.
根据多边形的内角和及正多边形的性质列式计算即可．
本题考查多边形的内角和及正多边形的性质，此为基础且重要知识点，必须熟练掌握．
12.【答案】稳定性
【解析】解：手机支架利用了三角形的稳定性，
故答案为：稳定性．
根据三角形具有稳定性解答即可．
本题考查的是三角形的性质，熟记三角形具有稳定性是解题的关键．
13.【答案】∠B=∠C
【解析】解：添加∠B=∠C，
在△ABE与△ACD中，
∠A=∠AAB=AC∠B=∠C，
∴△ABE≌△ACD(ASA)，
故答案为：∠B=∠C.
用“角边角”证明两个三角形全等，已知条件给出一组边相等和一组对应角相等，进而添加一组角相等即可．
本题考查的是三角形全等的判定，理解“角边角”定理是解题的关键．
14.【答案】20
【解析】解：∵水井到土地边沿的距离相等，则水井是三角形三个内角平分线的交点，
设水井的位置为点O，如图，
过O作OM⊥AC于M，ON⊥AB于N，OD⊥BC于D，
∵点O为三角形角平分线交点，
∴OM=ON=OD，
∵△ABC的面积=△OAB的面积+△OBC的面积+△OAC的面积，
∴△ABC的面积=12AB⋅ON+12BC⋅OD+12AC⋅OM=12(AB+BC+CA)⋅OD，
∵△ABC的周长是60，面积是600m2，
∴×60×OD=600，
∴OD=20，
即这口水井到土地边沿的距离是20m.
故答案为：20.
水井到土地边沿的距离相等，则水井是三角形三个内角平分线的交点，根据这块土地的面积是600m2求出距离即可．
本题考查角平分线的性质，三角形的面积，关键是由角平分线的性质得到OM=ON=OD，由三角形面积公式得到△ABC的面积=12(AB+BC+CA)⋅OD.
15.【答案】20
【解析】解：∵AD⊥AB，
∴∠BAD=90∘，
∵∠B=30∘，
∴BD=2AD，
∵∠B=∠C=30∘，
∴∠BAC=180∘−∠B−∠C=120∘，
∴∠DAC=∠BAC−∠BAD=30∘，
∴∠C=∠DAC，
∴AD=DC，
∴BD=2CD，
∵BC=30，
∴BD=20.
故答案为：20.
由垂直的定义得到∠BAD=90∘，由含30∘角的直角三角形的性质，得到BD=2AD，求出∠BAC=180∘−∠B−∠C=120∘，得到∠DAC=∠BAC−∠BAD=30∘，因此∠C=∠DAC，推出AD=DC，于是BD=2CD，即可求出BD的长，
本题考查含30∘角的直角三角形的性质，等腰三角形的性质，关键是由以上知识点推出BD=2CD.
16.【答案】10
【解析】解：连接PC，
∵EF是BC的垂直平分线，
∴BP=PC.
∴PA+BP=AP+PC.
∴当点A，P，C在一条直线上时，PA+BP有最小值，最小值=AC=10.
故答案为：10.
根据题意知点B关于直线EF的对称点为点C，故当点P在AC上时，AP+BP有最小值．
本题考查了轴对称-最短路线问题的应用，正确判断点A、P、C在一条直线上时，AP+PB有最小值是解题的关键．
17.【答案】2022.5
【解析】解：12a2−12b2
=12×20232−12×20222
=12×(20232−20222)
=12×(2023+2022)(2023−2022)
=12×4045
=2022.5.
故答案为：2022.5.
先提公因式，再用平方差公式进行计算即可．
本题主要考查了利用平方差公式因式分解进行简便运算，熟练掌握平方差公式是解题的关键．
18.【答案】x=1
【解析】解：由题意得：x2−1=0且x+1≠0，
解得：x=1，
故答案为：x=1.
根据分式值为零的条件是分子等于零且分母不等于零列式计算即可．
本题考查的是分式的值为零的条件，熟记分式值为零的条件是分子等于零且分母不等于零是解题的关键．
19.【答案】3
【解析】解：去分母，得ax−3=2x−2，
x=1a−2.
∵关于x的分式方程无解，
∴a=2，
∴最简公分母x−1=0，
∴x=1，
当x=1时，得a=3，
即a的值为3.
故答案为：3或2.
先把分式方程化为整式方程得到ax−3=2x−2，由于关于x的分式方程axx−1+31−x=2无解，则最简公分母x−1=0，求得x=1，进而得到a.
本题考查了分式方程的解：使分式方程左右两边成立的未知数的值叫分式方程的解．当分式方程无解时可能存在两种情况：(1)原分式方程存在增根；(2)原分式方程去分母后，整式方程无解．本题中由于原分式方程去分母后，得到的整式方程为一元一次方程，必定有解，所以只有一种情况．
20.【答案】1.4×10−3
【解析】解：0.0014g=1.4×10−3g.
故答案为：1.4×10−3.
绝对值小于1的数也可以利用科学记数法表示，一般形式为a×10−n，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数n由原数左边起第一个不为零的数字前面的0的个数所决定．
此题主要考查了用科学记数法表示较小的数，一般形式为a×10−n，其中1≤|a|