宁夏石嘴山市平罗中学2024届高三下学期第一次模拟考试数学（文）试卷(含答案)

这是一份宁夏石嘴山市平罗中学2024届高三下学期第一次模拟考试数学（文）试卷(含答案)，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题
1．已知集合，，则( )
A.B.C.D.
2．复数（其中i为虚数单位）的虚部为( )
A.2B.1C.D.
3．已知向量，，若与垂直，则( )
A.1B.C.2D.4
4．已知，分别是椭圆的左、右焦点，P为M上的一点，若，则( )
A.1B.2C.4D.8
5．设，则( )
A.B.C.D.
6．已知数列为等比数列且，，设等差数列的前n项和为，若，则( )
A.B.C.18D.2
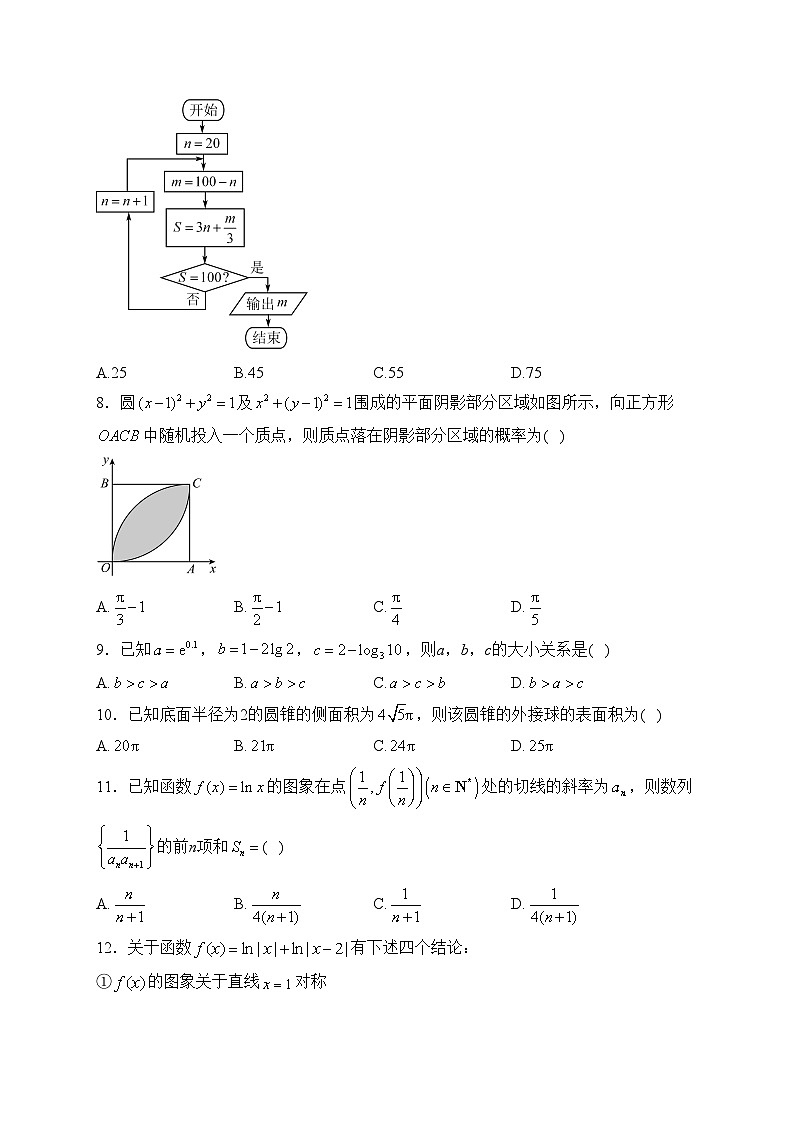
7．我国明朝数学家程大位著的《算法统宗》里有一道闻名世界的题目：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”如图所示的程序框图反映了对此题的一个求解算法，则输出的m的值为( )
A.25B.45C.55D.75
8．圆及围成的平面阴影部分区域如图所示，向正方形中随机投入一个质点，则质点落在阴影部分区域的概率为( )
A.B.C.D.
9．已知，，，则a，b，c的大小关系是( )
A.B.C.D.
10．已知底面半径为2的圆锥的侧面积为，则该圆锥的外接球的表面积为( )
A.B.C.D.
11．已知函数的图象在点处的切线的斜率为，则数列的前n项和( )
A.B.C.D.
12．关于函数有下述四个结论：
①的图象关于直线对称
②在区间单调递减
③的极大值为0
④有3个零点
其中所有正确结论的编号为( )
A.①③B.①④C.②③④D.①③④
二、填空题
13．已知等比数列的前n项和为，且，，则_______.
14．直线是双曲线的一条渐近线，双曲线的离心率是_______.
15．已知正数x,y满足，若恒成立，则实数m的取值范围为_______.
16．设函数的图象关于直线对称,它的周期是π,有下列说法:
①的函数图象过点;
②在上是减函数;
③的一个对称中心是;
④将的图象向右平移个单位长度得到函数的图象.
其中正确的序号是_______.（正确的序号全填上）
三、解答题
17．已知的内角A，B，C所对的边分别为a，b，c，设向量，，且.
（1）求角C；
（2）若，的面积为，求的周长.
18．如图，在四棱锥中，底面是正方形，且.
（1）若平面，，求三棱锥的体积；
（2）求证：.
19．我国老龄化时代已经到来，老龄人口比例越来越大，出现很多社会问题.2015年10月，中国共产党第十八届中央委员会第五次全体会议公报指出：坚持计划生育基本国策，积极开展应对人口老龄化行动，实施全面二孩政策.随着国家二孩政策的全面放开，为了调查一线城市和非一线城市的二孩生育意愿，某机构用简单随机抽样方法从不同地区调查了100位育龄妇女，结果如下表.
（1）求x和y的值.
（2）分析调查数据，是否有以上的把握认为“生育意愿与城市级别有关”？
（3）在以上二孩生育意愿中按分层抽样的方法，抽取6名育龄妇女，再选取两名参加育儿知识讲座，求至少有一名来自一线城市的概率.
参考公式：，
20．已知抛物线C：上一点M到其焦点的距离为3，到y轴的距离为2.
（1）求抛物线C的方程；
（2）若不过原点O的直线l：与抛物线C交于A，B两点，且，求实数m的值.
21．已知函数.
（1）当时，求曲线在点处的切线方程；
（2）若既存在极大值，又存在极小值，求实数a的取值范围.
22．在平面直角坐标系中，直线l的普通方程为；曲线C的参数方程是（为参数），以坐标原点为极点，x轴的正半轴为极轴，建立极坐标系.
（1）求直线l与曲线C的极坐标方程；
（2）直线与直线l与曲线C分别交于点A，B（点B与点O不重合），若，求的值.
23．已知函数.
（1）当时，求不等式的解集；
（2）若，求a的取值范围.
参考答案
1．答案：B
解析：因为，，
所以.
故选：B.
2．答案：A
解析：，
所以复数（其中i为虚数单位）的虚部为2.
故选：A.
3．答案：C
解析：由题可知，
因为与垂直，所以，解得，
所以，
故选：C.
4．答案：B
解析：因为，则，
由椭圆的定义可知：，
又因为，解得：.
故选：B.
5．答案：A
解析：由，
平方可得，
解得.
故选：A.
6．答案：C
解析：设数列的公比为q，则，所以，
所以，
所以.
故选：C.
7．答案：D
解析：执行程序框图：，，，
，，，继续执行；
，，，继续执行；
，，，继续执行；
，，，继续执行；
，，，继续执行；
，，，退出循环，输出.
故选：D.
8．答案：B
解析：圆及分别以和为圆心，
半径都是1.连接，可知阴影部分由分别以A，B为圆心，
1为半径的两个四分之一弓形组成，
阴影部分的面积为，
正方形的面积为，
所以质点落在阴影部分区域的概率为，
故选：B.
9．答案：B
解析：由题意可得：，
，且，则，
因为，则，
故选：B
10．答案：D
解析：如图，设圆锥的母线长为，由圆锥的侧面积公式，得，
解得，所以圆锥的高为.
设圆锥的外接球半径为R，则在中，由勾股定理，，解得，
所以该圆锥的外接球的表面积为.
故选：D.
11．答案：A
解析：由，所以函数在点处的切线斜率，
，
所以.
故选：A.
12．答案：D
解析：函数的定义域为，
对于①，，则，
，的图象关于直线对称，①正确；
对于②，当时，，在单调递增，②不正确；
对于③，当时，，在单调递减，
当时，，在上单调递增，在上单调递减，
又在单调递增，因此在处取极大值，③正确；
对于④，由得：，即或，解得或，
于是得有3个零点，④正确，
所以所有正确结论的编号为①③④.
故选：D
13．答案：121
解析：设公比为q，故，解得，
所以，
故.
故答案为：121.
14．答案：2
解析：双曲线的一条渐近线方程为，可得，即
解得.故答案为2.
15．答案：
解析：因为，且，所以，
当且仅当时取等号.
因为不等式恒成立，
所以，解得.
故答案为：.
16．答案：①③
解析：依题意，，解得，因的函数图象关于直线对称，
则，，而，于是得，，因此，
因，即的函数图象过点，①正确；
当时，，而正弦函数在上不单调，②不正确；
因，的一个对称中心是，③正确；
，则将的图象向右平移个单位长度得到函数为，
显然不是函数，④不正确，
所以正确的序号是①③.
故答案为：①③.
17．答案：（1）
（2）
解析：（1）由向量平行的坐标公式，得，
由正弦定理，得，即，
由余弦定理，得，又，故.
（2）由三角形面积公式，得，故，
所以为等腰三角形，所以.
将代入（1）中所求，则，
解得（舍去）或，
所以的周长为.
18．答案：（1）
（2）证明见解析
解析：（1），，
.
（2）如图，连接，交于点O，连接，
四边形为正方形，，
又，O为的中点，，
，且、平面，
平面，
又平面，.
19．答案：（1）,
（2）有以上的把握认为“生育意愿与城市级别有关”
（3）
解析：（1）由题意得，.
（2）由，得，
有以上的把握认为“生育意愿与城市级别有关”.
（3）抽取6名育龄妇女，来自一线城市的人数为，记为1，2，
来自非一线城市的人数为，记为a，b，c，d，
选设事件A为“取两名参加育儿知识讲座，求至少有一名来自一线城市”，
基本事件为：，,,,,,,,,,,，,,,
事件,,,,,,,,共有9个，
或.
20．答案：（1）
（2）
解析：（1）由题意知，点M到准线的距离为3，
所以，解得.
故C的方程为.
（2）设，，由得，
所以，，
，.
因为，所以，
即，解得或0.
又直线l不过原点O，所以.
又满足要求，所以.
21．答案：（1）
（2）
解析：（1）当时，函数，求导得，则，而，
所以曲线在点处的切线方程为，即.
（2）函数的定义域为，
求导得，
当时，，由，得，由，得，
则函数在上递增，在上递减，函数只有极大值，不合题意；
当时，由，得或，
①若，即，由，得或，由，得，
则函数在,上递增，在上递减，
因此函数的极大值为，极小值为，符合题意；
②若，即，由，得或，由，得，
则函数在,上递增，在上递减，
因此函数的极大值为，极小值为，符合题意；
③若，即，由在上恒成立，得在上递增，
函数无极值，不合题意，
所以a的取值范围为.
22．答案：（1），
（2）
解析：（1）由，，得直线l的极坐标方程为.
由，得曲线C的普通方程为，
即，
由，，得曲线C的极坐标方程为.
（2）把代入，得，
把代入，得，
，，
即，
，解得，
又，.
23．答案：（1）
（2）
解析：（1）当时，.
若，则当时，，故，
当时，，故，
又因为当时，，
所以不等式的解集为.
（2）由题设可得，
所以或.
当时，，故.
当时，，故.
综上，a的取值范围是.
非一线
一线
总计
愿生
40
y
60
不愿生
x
22
40
总计
58
42
100
0.050
0.010
0.001
k
3.841
6.635
10.828