2024年甘肃省武威市凉州区武威第五中学教研联片中考模拟一模数学试题

这是一份2024年甘肃省武威市凉州区武威第五中学教研联片中考模拟一模数学试题，共12页。试卷主要包含了选择题，填空题，计算题，作图题，解答题等内容，欢迎下载使用。
一、选择题(共30分)
1．（3分）已知二次函数y=x2+bx-4图象上A、B两点关于原点对称，若经过A点的反比例函数的解析式是y=8x，则该二次函数的对称轴是直线（ ）
A．x=1B．x=2C．x=-1D．x=-2
2．（3分）反比例函数y=8x图象上有三个点（x1，y1），（x2，y2），（x3，y3），其中x1＜x2＜0＜x3，则y1，y2，y3的大小关系是（ ）
A．y1＜y2＜y3B．y2＜y1＜y3C．y3＜y1＜y2D．y3＜y2＜y1
3．（3分）两个相似多边形一组对应边分别为3 cm，4.5 cm，那么它们的相似比为（ ）
A．23B．32C．49D．94
4．（3分）如图，AB//CD，AD，BC相交于点O.若AB=1，CD=2，BO：CO=（ ）
A．1：2B．1：4C．2：1D．4：1
5．（3分）如图，矩形ABCD中，点A在双曲线y=-8x上，点B，C在x轴上，延长CD至点E，使CD=2DE，连接BE交y轴于点F，连接CF，则△BFC的面积为（ ）
A．5B．6C．7D．8
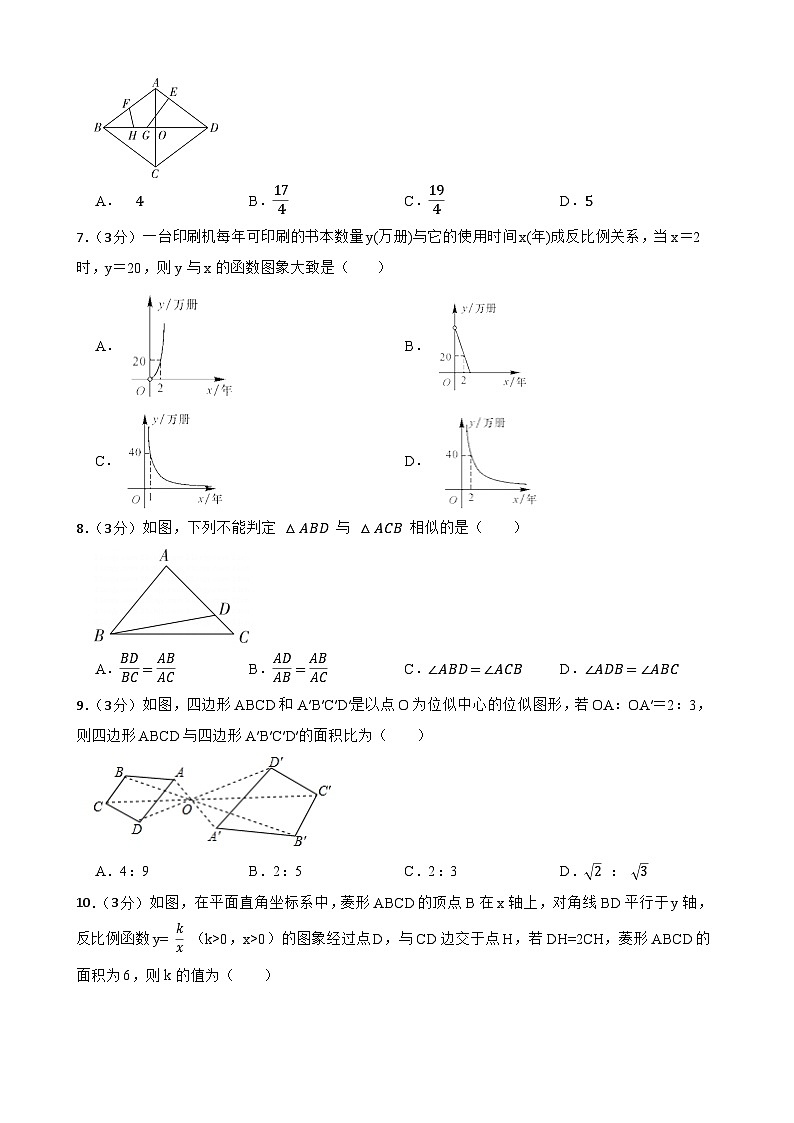
6．（3分）如图，已知菱形ABCD的对角线AC，BD相交于点O，AC=6，BD=8，点E在AD上，AEDE=13，点F为AB的中点，点G，H为BD上的动点，GH=1，连接FH，EG，则FH+EG的最小值为（ ）
A． 4B．174C．194D．5
7．（3分）一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系，当x＝2时，y＝20，则y与x的函数图象大致是（ ）
A．B．
C．D．
8．（3分）如图，下列不能判定 △ABD 与 △ACB 相似的是（ ）
A．BDBC=ABACB．ADAB=ABACC．∠ABD=∠ACBD．∠ADB=∠ABC
9．（3分）如图，四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形，若OA：OA′＝2：3，则四边形ABCD与四边形A′B′C′D′的面积比为（ ）
A．4：9B．2：5C．2：3D．2 ： 3
10．（3分）如图，在平面直角坐标系中，菱形ABCD的顶点B在x轴上，对角线BD平行于y轴，反比例函数y= kx （k>0，x>0）的图象经过点D，与CD边交于点H，若DH=2CH，菱形ABCD的面积为6，则k的值为（ ）
A．2B．4C．6D．8
二、填空题(共24分)
11．（3分）已知反比例函数y=8x的图象经过点A(m，-4)，则A关于y轴的对称点A'坐标为 .
12．（3分）已知两个相似多边形的周长比为1：2，它们的面积和为100，则较小多边形的面积是 ．
13．（3分）实验表明，当导线的长度一定时，导线的电阻与它的横截面积成反比例．一条长为100 cm的导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示，那么，其函数关系式为 ，当S＝2 cm2时， R= (Ω)
14．（3分）如图，在等腰△ABC中，AB=AC=9，BP=13BC=2，D在AC上，且∠APD=∠B，则CD= ．
15．（3分）如图，已知正方形ABCD中，AB=2，点E为BC边上一动点(不与点B、C重合)，连接AE，将AE绕点E顺时针旋转90°得到EF，连接CF，连接AF与CD相交于点G，连接DF，当DF最小时，四边形CEGF的面积是 ．
16．（3分）如图，在Rt△ABC中，∠ACB= 90°，CD⊥AB于点D， AD=95， BD= 165，则sinB= .
17．（3分）若xy=12，则x+yy= .
18．（3分）如图，A、B是函数y＝6x上两点，P为一动点，作PB∥y轴，PA∥x轴，下列说法：①△AOP≌△BOP；②S△AOP＝S△BOP；③若OA＝OB，则OP平分∠AOB；④若S△BOP＝2，则S△ABP＝4，正确有 （填序号）
三、计算题(共8分)
19．（1）（4分）计算：(-13)-1+(-1)2022+(3.14-π)0-|2cs30°-1|；
（2）（4分）解不等式组3(x-1)≤2x-2x+33+1>x+22，并将其解集在数轴上表示出来.
四、作图题(共6分)
20．（6分）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABC的三个顶点坐标分别为A（-3，1），B（-1，1），C（0，3）.
（ 1 ）（2分）画出△ABC关于y轴对称的△ A1B1C1 ；
（ 2 ）（2分）画出△ABC以点O为位似中心的位似图形△ A2B2C2 ，△ABC与△ A2B2C2 的位似比为1：2；
（ 3 ）（2分）求以 B1 、 B2 、 A1 、 A2 四个点为顶点构成的四边形的面积.
五、解答题(共52分)
21．（5分）一个不透明的布袋里装有3个白球，1个黑球和若干个红球，它们除颜色外其余都相同，从中任意摸出1个球，是白球的概率12.
（1）（3分）布袋里红球有多少个?
（2）（3分）先从布袋中摸出1个球后不放回，再摸出1个球，请用列表或画树状图等方法求出两次摸到的球都是白球的概率.
22．（6分）如图，一次函数y1=mx+n的图像与x轴、y轴分别交于A，B两点，与反比例函数y2=kx的图像分别交于C，D两点，已知点C的坐标是(1，-3)，且AB=2BC，求一次函数与反比例函数的解析式．
23．（8分）如图所示，点D在三角形ABC的边AB上，DE交AC于点E，∠ADE=∠B，点F在AD上，且AD2=AF·AB.求证：
（1）（4分）ADAB=AEAC；
（2）（4分）△AEF∽△ACD.
24．（6分）如图，▱ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F.
（1）（3分）求证：▱ABEF是菱形：
（2）（3分）若▱ABCD∽▱FDCE，则BCCD的值为 .
25．（8分）如图，在Rt△ABC中，∠C=90°，以AC为直径的⊙O交AB于点E，D是BC上一点，连接DE，且∠B=∠BED．
（1）（4分）求证：ED是⊙O的切线；
（2）（4分）若BE=16，ED=10，求AC的长．
26．（9分）如图1，在正方形ABCD中，P是边BC上的动点，E在△ABP的外接圆上，且位于正方形ABCD的内部，EA=EP，连结AE，EP．
（1）（3分）求证：△PAE是等腰直角三角形；
（2）（3分）如图2，连结DE，过点E作EF⊥BC于点F，请探究线段DE与PF的数量关系，并说明理由；
（3）（3分）当点P是BC的中点时，DE=4，求BC的长。
27．（10分）如图，在平面直角坐标系中，A点的坐标为(a，8)，AB⊥x轴于点B，ABOB=43，反比例函数y=kx的图象的一支分别交AO，AB于点C，D，延长AO交反比例函数的图象的另一支于点E，已知点D的纵坐标为2．
（1）（3分）求反比例函数的表达式及点E的坐标；
（2）（3分）连接CD，OD，求S△OCD；
（3）（4分）在x轴上是否存在两点M，N(M在N的左侧)，使以E，M，C，N为顶点的四边形为矩形？若存在，求出矩形的周长；若不存在，说明理由．
答案
1-5 C B A A B 6-10 B C A A D
11．(2，-4)
12．20
13．R= 29S；4.5
14．89
15．43
16．35
17．
18．②③④
19．（1）-3
（2）x≤1，
解集表示在数轴上，如图所示：
.
20．（1）∵A（-3，1），B（-1，1），C（0，3），确定关于y轴的对称点坐标分别为 A1 （3，1）， B1 （1，1）， C1 （0，3），
∴△ABC关于y轴对称的△ A1B1C1 如图所示；
（2）∵A（-3，1），B（-1，1），C（0，3），点O为位似中心，位似比为1：2
∴位似变化对应点的坐标为 A2 （6，-2）， B2 （2，-2）， C2 （0，－6），
作图，如图所示|
（3）9.
21．（1）布袋里的红球有2个；
（2）画树状图如下：
由树状图可知共有30种均等可能结果，两次摸到的球都是白球的有6种可能
∴P（摸得两白）=630=15.
22．y1=-x-2．
23．（1）∵∠ADE=∠B，
∴DE∥BC.
∴ADAB =AEAC.
（2）∵AD2=AF·AB，
∴ADAB =AFAD.
由(1)，得ADAB =AEAC.
∴AEAC =AFAD.
∵∠A=∠A，
∴△AEF∽△ACD.
24．（1）∵∠BAD的平分线交BC于点E，
∴∠BAE=∠EAF.
∵四边形ABCD是平行四边形，
∴AD∥BC.
∴∠EAF=∠AEB.
∴∠BAE=∠AEB.
∴AB=BE.
同理，AB=AF.
∴BE=AF.
∵AD∥BC
∴四边形ABEF是平行四边形.
∵AB=BE，
∴四边形ABEF是菱形.
（2）1+52
25．（1）证明：如图1，连接OE．
图1
∵∠C=90°，∴∠A+∠B=90°．
又∵OA=OE，∴∠A=∠AEO．
∵∠B=∠BED，∴∠AEO+∠BED=90°，
∴∠OED=90°，∴OE⊥ED，∴ED是⊙O的切线．
（2）如图2，连接CE．
图2
∵∠B=∠BED，∴BD=ED=10．
∵AC是⊙O的直径，∠ACB=90°，∴∠BEC=90°，CD是⊙O的切线．
又∵ED是⊙O的切线，∴CD=ED=10，∴BC=BD+CD=20．
在Rt△BEC中，CE=BC2-BE2=202-162=12．
设AE=x．
在Rt△AEC中，AC2=AE2+CE2=x2+122；
在Rt△ABC中，AC2=AB2-BC2=(x+16)2-202，
∴x2+122=(x+16)2-202，解得x=9，∴AC=92+122=15．
26．（1）如图1，∵点E在△ABP的外接圆上，
∴∠AEP+∠A=180°，
∴∠AEP=90°，
∴∠EAP+∠EPA=90°．
∵EA=EP，
∴∠EAP=∠EPA=45°，
∴△PAE是等腰直角三角形；
（2）结论：DE=2PF，
理由：如图2，延长FE交AD于点H，
∵EF⊥BC，BC//AD，
∴EH⊥AD，
即∠AHE=∠EFP=90°，
∴∠EAH+∠AEH=90°，
∵∠AEP=90°，
∴∠PEF+∠AEH=90°，
∴∠EAH=∠PEF，
又∵△PAE是等腰直角三角形，
∴EA=EP，
∴△EAH≌△PEF(AAS)，
∴AH=EF，EH=PF，
∵AD=DC=HF，
∴AH+HD=EF+HE，
∴HD=HE=PF，
∴DE=2HE=2PF；
（3）解：解：①由(2)知DE=2PF．
∵DE=4，
∴PF=22．
∵P是BC的中点，
∴BC=2PC=82，
27．（1）C(3，4)，E(-3，-4)；
（2）9；
（3）在x轴上存在两点M，N，使以E，M，C，N为顶点的四边形为矩形，理由如下：
∵设M(m，0)，N(-m，0)，
∴OM=ON，
∵C(3，4)，E(-3，-4)，
∴OC=OE，
∴四边形EMCN是平行四边形，
当MN=CE=2OC=2×32+42=10时，
∴OM=ON=5，即m=5或-5，
∴OM=ON=OC，
∴∠OMC=∠OCM，∠ONC=∠OCN，
∵∠OMC+∠OCM+∠ONC+∠OCN=180°，
∴∠OCM+∠OCN=90°，即∠MCN=90°，
∴此时平行四边形EMCN为矩形，
∵M在N的左侧，
∴m=-5，
∴CM=(3+5)2+42=45，CN=(3-5)2+42=25，
∴矩形EMCN周长为(45+25)×2=125．