2024年广东省湛江市霞山区实验中学中考一模数学试题(无答案)

这是一份2024年广东省湛江市霞山区实验中学中考一模数学试题(无答案)，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（每小题3分，共30分）
1.实数4的相反数是（ ）
A.B.C.D.4
2.围棋在古代被列为“琴棋书画”四大文化之一，蕴含着中华文化的丰富内涵，如图所示是一个无盖的围棋罐，其主视图为（ ）
A.B.C.D.
3.若二次根式在实数范围内有意义，则实数x的取值范围是（ ）
A.B.C.D.
4.下列计算正确的是（ ）
A.B.
C.D.
5.在物理学上，压力、压强与受力面积之间有如下关系式：.当F为定值时，下列图中，能大致表示压强P与受力面积S之间函数关系的是（ ）
A.B.C.D.
6.如图，在中，，点D、E分别是直角边、的中点，连接，则的度数是（ ）
第6题图
A.70°B.60°C.30°D.20°
7.不等式组的解集在数轴上表示正确的是（ ）
A.B.C.D.
8.关于二次函数，下列说法正确的是（ ）
A.图象的对称轴是直线
B.图象与x轴有两个交点
C.当时，y随x的增大而增大
D.当时，y取得最大值，且最大值为3
9.如图，、是的两条弦，且，过点C作的切线交的延长线于点D.若的半径为2，则阴影部分的面积为（ ）
第6题图
A.B.C.D.
10.如图，在中，，，以A为圆心，任意长为半径画弧分别交、于点M和N，再分别以M、N为圆心，大于的长为半径画弧，两弧交于点P，连接并延长交于点D，则下列说法中正确的个数是（ ）
①平分；②；③点D在的垂直平分线上；④.
第10题图
A.1B.2C.3D.4
二、填空题（每小题3分，共18分）
11.第七次全国人口普查结果显示，我国具有大学文化程度的人口超218000000人.数字2180000000用科学记数法表示为______.
12.若关于x的一元二次方程有一个根为，则m的值为______.
13.分解因式：______.
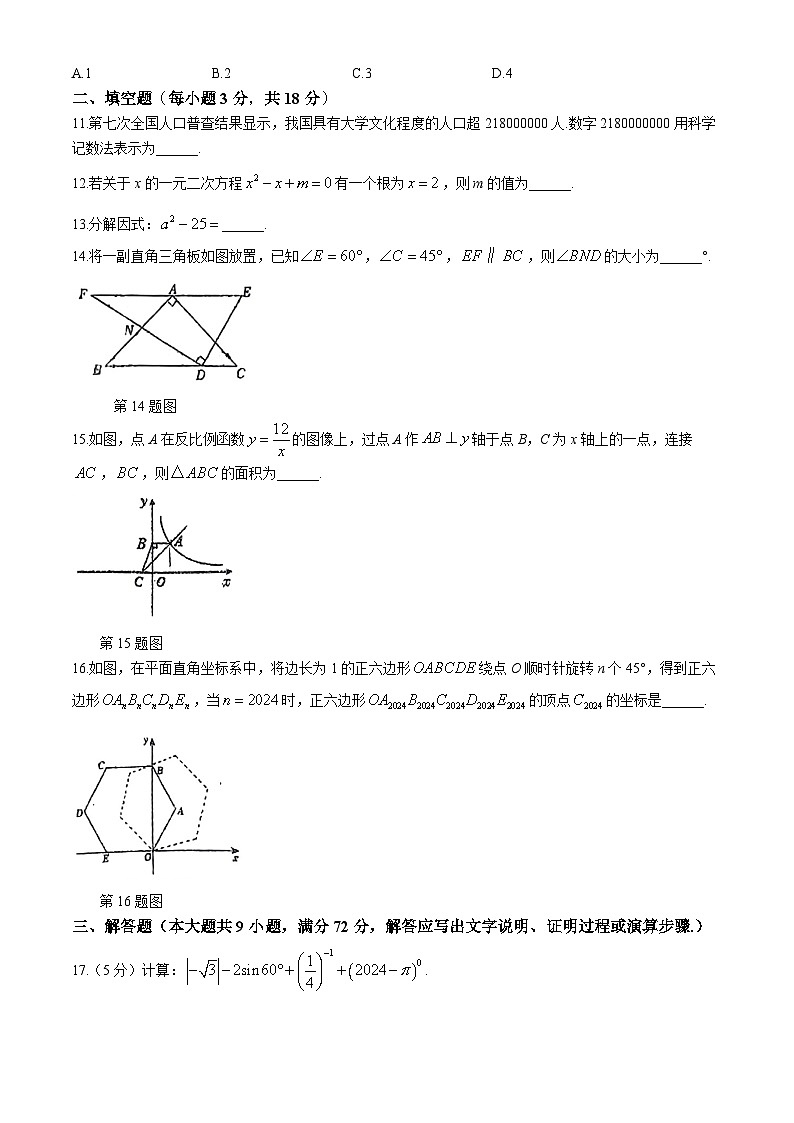
14.将一副直角三角板如图放置，已知，，，则的大小为______°.
第14题图
15.如图，点A在反比例函数的图像上，过点A作轴于点B，C为x轴上的一点，连接，，则的面积为______.
第15题图
16.如图，在平面直角坐标系中，将边长为1的正六边形绕点O顺时针旋转n个45°，得到正六边形，当时，正六边形的顶点的坐标是______.
第16题图
三、解答题（本大题共9小题，满分72分，解答应写出文字说明、证明过程或演算步骤.）
17.（5分）计算：.
18.（5分）下面是小亮化简分式的部分运算过程：
解：原式……第①步.
……第②步.
……
（1）小亮运算过程中第______步出现了错误；
（2）请写出正确且完整的解答过程.
19.（6分）2022年3月25日，教育部印发《义务教育课程方案和课程标准（2022年版）》，优化了课程设置，将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况，随机抽取部分学生调查了他们一周的课外劳动时间，将数据进行整理并制成如下统计图。
图1 图2
请根据图中提供的信息，解答下列的问题：
（1）求图1中的______，本次调查数据的中位数是______h，本次调查数据的众数是______h；
（2）若该校共有2000名学生，请根据统计数据，估计该校学生一周的课外劳动时间不小于的人数.
20.（6分）如图，平分，.
（1）求证：；
（2）若，，求的长.
21.（8分）为建设美好公园社区，增强民众生活幸福感，某社区服务中心在文化活动室墙外安装遮阳篷，便于社区居民休憩.如图，在侧面示意图中，遮阳篷AB长为5米，与水平面的夹角为16°，且靠墙端离地高BC为4米，此时太阳光线AD与地面CE的夹角为45°.（参考数据：，，）
（1）据研究，当一个人从遮阳篷进出时，如果遮阳篷外端（即图中A）到地面的距离小于2.3m时，则人进出时总会觉得没有安全感，就会不自觉的低下头或者用手护着头，请你通过计算，判断人进出此遮阳篷时是否有安全感；
（2）求阴影CD的长.（结果精确到0.1米）
22.（8分）某校从商场购进A、B两种品牌的营养早餐牛奶，购买A品牌牛奶花费了1500元，购买B品牌牛奶花费了1000元，且购买A品牌牛奶的数量是购买B品牌牛奶数量的2倍.已知购买一公斤B品牌牛奶比购买一公斤A品牌牛奶多花20元.
（1）问购买一公斤A品牌、一公斤B品牌的牛奶各需多少元？
（2）该校决定再次购进A、B两种品牌牛奶共20公斤，恰逢商场对两种品牌牛奶的售价进行调整，A品牌牛奶售价比第一次购买时提高了5%，B品牌牛奶按第一次购买时售价的9折出售，如果该校此次购买A、B两种品牌牛奶的总费用不超过1350元，那么该校此次最多可购买多少公斤B品牌牛奶？
23.（10分）如图，在中，，点D为边的中点，以为直径作，分别与、交于点E、F，过点E作于G.
（1）求证：是的切线；
（2）若，的直径为5，求的长.
24.（12分）【建立模型】（1）如图1，点B是线段上的一点，，，，垂足分别为C，B，D，.求证：；
【类比迁移】（2）如图2，点在反比例函数图象上，连接，将绕点O逆时针旋转90°到，若反比例函数经过点B.求反比例函数的解析式；
【拓展延伸】（3）如图3抛物线与x轴交于A，B两点（点A在点B的左侧），与y轴交于C点，已知点，连接，抛物线上是否存在点M，便得，若存在，求出点M的横坐标.
图1 图2 图3 备用图
25.（12分）如图，在中，，，，动点P从点A出发（动点P不与的顶点重合），沿折线以每秒5个单位的速度向终点B运动，过点P作于点D，以点P为直角顶点作，使与点P所在的直角边平行，设点P的运动时间为t（秒）.
备用图1 备用图2
（1）直接写出______；当点P落在边上时，的长为______（用含t的代数式表示）；
（2）当点E落在边上时，求t的值；
（3）当的两条直角边所在的直线截所得的两个三角形全等时，求与重叠部分图形的周长.