浙江省金华市2022—2023学年七年级下学期数学期中试卷

这是一份浙江省金华市2022—2023学年七年级下学期数学期中试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本题有10小题，每小题3分，共30分）
1．下列方程中，属于二元一次方程的是（ ）
A．x2-y=1B．x+1y=2C．2x+y=3zD．2x+3y=4
2．将图中的叶子平移后，可以得到的图案是（ ）
A．B．
C．D．
3．一张普通A4纸的厚度约为0.000104m，数0.000104用科学记数法可表示为（ ）
A．1.04×10-2B．1.04×10-3C．1.04×10-4D．1.04×10-5
4．下列运算正确的是（ ）
A．a3⋅a2=a5B．(a2)3=a5C．(ab)2=ab2D．a3+a2=a5
5．下列各式从左到右的变形中，属于因式分解的是（ ）
A．6x2y＝2x•3xyB．x2+4x+1＝x（x+4）+1
C．(a+3)(a-3)＝a2-9D．x2－2xy＝x（x－2y）
6．如图，已知直线a，b被直线c所截，且a∥b，若∠1＝70°，则∠2的度数是（ ）
A．130°B．110°C．80°D．70°
7．下列四组值中，不是二元一次方程x-2y=1的解的是（ ）
A．x=1y=1B．x=0y=-0.5C．x=1y=0D．x=-1y=-1
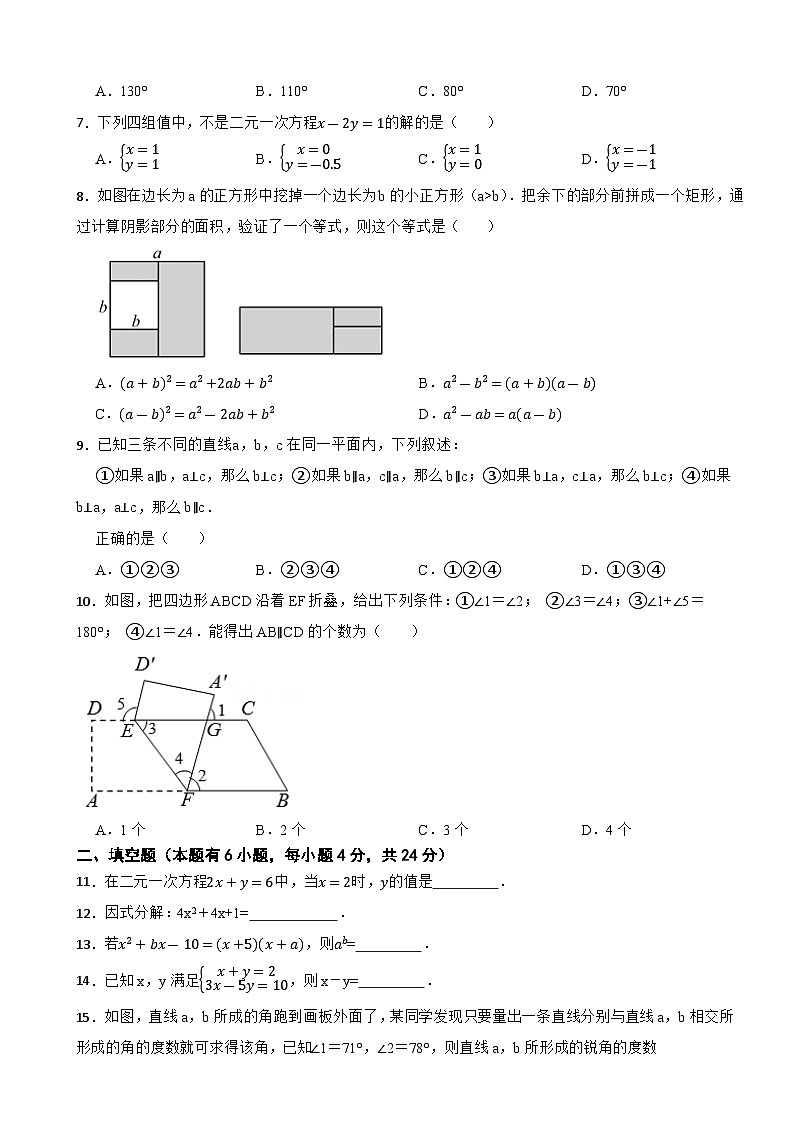
8．如图在边长为a的正方形中挖掉一个边长为b的小正方形（a>b）．把余下的部分前拼成一个矩形，通过计算阴影部分的面积，验证了一个等式，则这个等式是（ ）
A．(a+b)2=a2+2ab+b2B．a2-b2=(a+b)(a-b)
C．(a-b)2=a2-2ab+b2D．a2-ab=a(a-b)
9．已知三条不同的直线a，b，c在同一平面内，下列叙述：
①如果a∥b，a⊥c，那么b⊥c；②如果b∥a，c∥a，那么b∥c；③如果b⊥a，c⊥a，那么b⊥c；④如果b⊥a，a⊥c，那么b∥c．
正确的是（ ）
A．①②③B．②③④C．①②④D．①③④
10．如图，把四边形ABCD沿着EF折叠，给出下列条件：①∠1＝∠2； ②∠3＝∠4；③∠1+∠5＝180°； ④∠1＝∠4．能得出AB∥CD的个数为（ ）
A．1个B．2个C．3个D．4个
二、填空题（本题有6小题，每小题4分，共24分）
11．在二元一次方程2x+y=6中，当x=2时，y的值是 ．
12．因式分解：4x2＋4x+1= ．
13．若x2+bx-10=(x+5)(x+a)，则ab= ．
14．已知x，y满足x+y=23x-5y=10，则x－y= ．
15．如图，直线a，b所成的角跑到画板外面了，某同学发现只要量出一条直线分别与直线a，b相交所形成的角的度数就可求得该角，已知∠1＝71°，∠2＝78°，则直线a，b所形成的锐角的度数为 °．
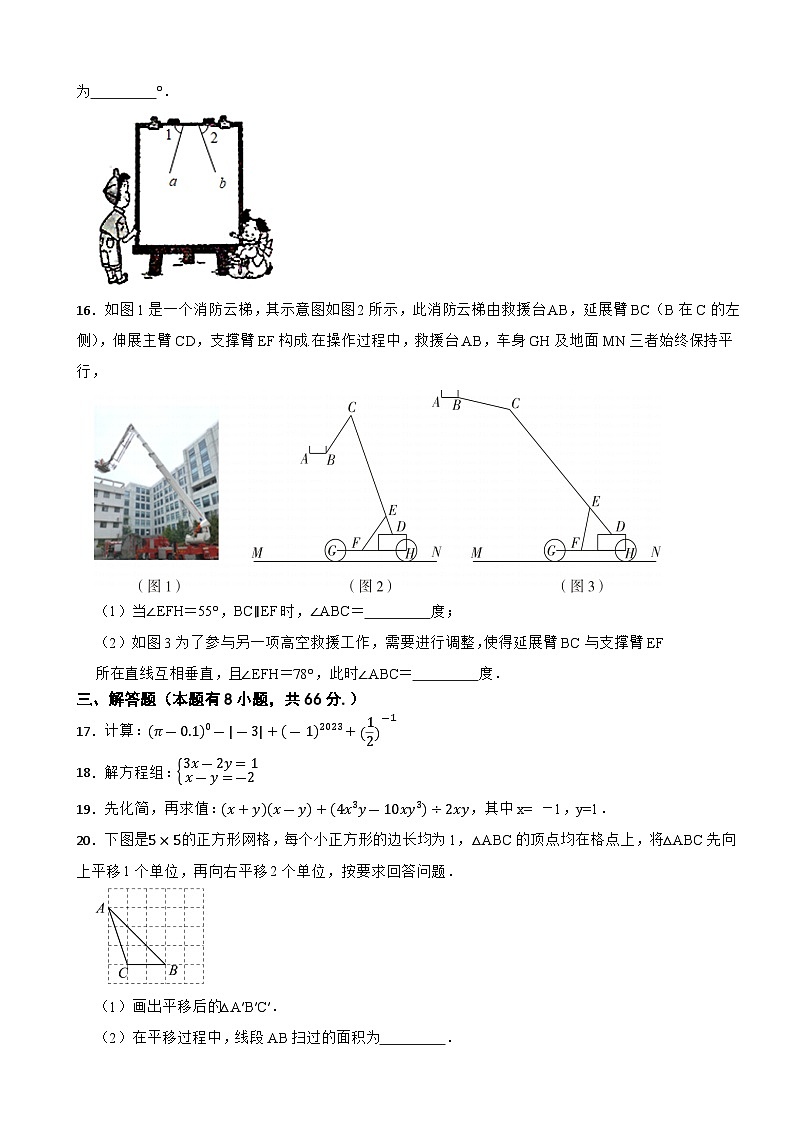
16．如图1是一个消防云梯，其示意图如图2所示，此消防云梯由救援台AB，延展臂BC（B在C的左侧），伸展主臂CD，支撑臂EF构成.在操作过程中，救援台AB，车身GH及地面MN三者始终保持平行，
（1）当∠EFH＝55°，BC∥EF时，∠ABC＝ 度；
（2）如图3为了参与另一项高空救援工作，需要进行调整，使得延展臂BC与支撑臂EF
所在直线互相垂直，且∠EFH＝78°，此时∠ABC＝ 度．
三、解答题（本题有8小题，共66分.）
17．计算：(π-0.1)0-|-3|+(-1)2023+(12)-1
18．解方程组：3x-2y=1x-y=-2
19．先化简，再求值：(x+y)(x-y)+(4x3y-10xy3)÷2xy，其中x= －1，y=1．
20．下图是5×5的正方形网格，每个小正方形的边长均为1，△ABC的顶点均在格点上，将△ABC先向上平移1个单位，再向右平移2个单位，按要求回答问题．
（1）画出平移后的△A′B′C′．
（2）在平移过程中，线段AB扫过的面积为 ．
21．如图，一个长方形中剪下两个大小相同的正方形（有关线段的长如图所示），留下一个“T”型的图形（阴影部分）
（1）用含x，y的代数式表示“T”型图形的面积并化简．
（2）若x=7米，y=21米，“T”型区域铺上价格为20元/m2的草坪，请计算草坪的造价．
22．如图，在四边形ABCD中，AD∥BC，BD⊥CD，点E，F分别在BC，CD上，EF⊥CD．
（1）判断∠1与∠2的大小关系，并说明理由．
（2）若∠A＝100°，BD平分∠ABC，求∠ADC的度数.
23．水果商贩老徐到“水果批发市场”进货，草莓的批发价格是60元/箱，苹果的批发价格是40元/箱．现购得草莓和苹果共60箱，刚好花费3100元．
（1）问草莓、苹果各购买了多少箱？
（2）商贩老徐有甲、乙两家店铺，每售出一箱草莓和苹果，甲店分别获利15元和20元，乙店分别获利12元和16元．老徐将购进的60箱水果分配给甲店草莓a箱（a＞0），苹果b箱（b＞0），其余均分配给乙店．由于他口碑良好，两家店都很快卖完了这批水果．
①若老徐在甲店获利600元，求他在乙店获利多少元？
②在本次买卖中，老徐希望能获得1100元的总利润，通过计算说明老徐的希望能否实现.
24．如图，已知直线MN，PQ交直线l分别于点A，B，MN∥PQ，∠MAB=60°，AC平分∠MAB交PQ于点C，过点B作BD⊥AC于点D．将△BCD绕点C按顺时针方向以每秒2度的速度旋转得到△CB1D1，同时△ABD绕点A按逆时针方向以每秒4度的速度旋转得到△AB2D2，旋转时间为t秒，当 B1时首次落在AC的延长线上时，两个三角形都停止转动．
（1）比较大小：∠CAB ∠ACB．(填“＞”或“＜”或“＝”）
（2）若直线l平分∠D2AB2时，求∠DCD1的度数．
（3）在旋转过程中，是否存在某一时刻，使得CD1与△AB2D2的某一边平行？若存在，求旋转时间t的值；若不存在，请说明理由．
答案解析部分
1．【答案】D
2．【答案】A
3．【答案】C
4．【答案】A
5．【答案】D
6．【答案】B
7．【答案】A
8．【答案】B
9．【答案】C
10．【答案】C
11．【答案】2
12．【答案】(2x+1)2
13．【答案】-8
14．【答案】3
15．【答案】31
16．【答案】（1）125
（2）168
17．【答案】解：原式= 1-3-1+2
=－1
18．【答案】解：3x-2y=1①x-y=-2②
由②得x=y-2③，
把③代入①得：3（y-2）-2y=1，
解得：y=7，
把y=7代入①得：x=5，
∴方程组的解为：x=5y=7；
19．【答案】解：原式= 3x2-6y2
当x=－1，y=1时，原式=－3
20．【答案】（1）解：如图， △A′B′C′ 即为所求；
（2）9
21．【答案】（1）解：S= (x+2y)(2x+y)-2y2=2x2+5xy
（2）解：当x=7，y=21时，S=833m2
造价为20×883=1660元.
22．【答案】（1）解：∠1=∠2
理由： ∵BD⊥CD，EF⊥CD，
∴BD∥EF，
∴∠2=∠DBE，
∵ AD∥BC ，
∴∠1=∠DBE，
∴∠1=∠2.
（2）解：∵AD∥BC ， ∠A＝100° ，
∴∠ABC=180°-∠A＝80° ，
∵BD平分∠ABC，
∴∠DBC=12∠ABC=40°，
由（1）知∠1=∠DBC=40°，
∴ ∠ADC =∠1+∠BDC=40°+90°=130°；
23．【答案】（1）解：设草莓购买了x箱，则苹果购买了（60-x）箱，
60x+40（60-x）=3100，
解得：x=35，
60-x=25箱
答：草莓购买了35箱，苹果购买了25箱；
（2）解：①甲店所获利润为（15a+20b)元，由题意：15a+20b=600，
即3a+4b=200
乙店所获利润为12（35－a）+16（25－b）=420－12a-16b=420－4(3a+4b)
把3a+4b=200，代入得，420－4(3a+4b)=420－4×200=340元.
答：他在乙店获利340元.
②不能，理由：由①知：15a+20b+12（35－a）+16（25－b）=1100，
化简得3a+4b=280，
∴b=70-34a，
由题意知0＜a≤35，0＜b≤25且a、b为正整数，
即0＜70-34a≤25，解得a≥60，不符合题意，
∴ 老徐的不望能否实现.
24．【答案】（1）=
（2）解：∵∠MAB=60°，AC平分∠MAB，
∴∠DAB=12∠MAB=30°，
①当旋转后△AB2D2在平行线之间，如图，
∵直线l平分∠D2AB2，
∴△ABD绕点A逆时针方向旋转的角度为∠B2AB=12∠DAB=15°，
∴旋转时间为154秒，
∴△BCD绕点C顺时针方向旋转的角度为154×2=7.5°；
②当旋转后△AB2D2在平行线之外，
∵直线l平分∠D2AB2，
∴∠B2AE=12∠DAB=15°，
∴△ABD绕点A逆时针方向旋转的角度为180°+∠B2AE=195°，则旋转时间为1954秒，
∴△BCD绕点C顺时针方向旋转的角度为1954×2=97.5°；
∴ ∠DCD1的度数为 7.5°或97.5° ；
（3）解：设旋转时间为t，①如图，当CD1∥AD2，
∴∠DCD1+∠DAD2=180°，
∴2t+4t=180°， 解得：t=30，
当CD1∥AD2，则∠DCD1=∠DAD2=2t，
∴△ABD绕点A逆时针方向旋转的角度为360°+∠D2AB2=360°-2t，
即360°-2t=4t，解得t=60；
②如图，当CD1∥AB2，
∴∠DCD1+∠DAB2=180°，即∠DCD1+∠DAD2=150°，
∴2t+4t=150°， 解得：t=25，
当CD1∥AB2，则∠DAB2=∠DCD1=2t，
∵△ABD绕点A逆时针方向旋转的角度为360°+∠D2AB2=360°-2t-30°，
∴330-2t=4t，解得：t=55，
③当CD1∥D2B2，如图，延长D2B2交PQ于k，
∴∠1=∠BCD1=∠D1CD-30°，
由题意知：∠ADB=90°，∠A2DK=90°，∠DAD2=4t，∠D1CD=2t，
∴∠DAD2+∠1=180°，
∴2t+4t-30=180，解得t=35，
综上可得：t= 25或30或45或55或60 。