江苏省泰州市靖江市高级中学2023-2024学年高二下学期3月数学试题（Word版附解析）

这是一份江苏省泰州市靖江市高级中学2023-2024学年高二下学期3月数学试题（Word版附解析），共29页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的选项中，只有一项是符合题目要求的．
1. 如图，在三棱柱中，，分别是，的中点，，则（ ）
A. 1B. C. 0.5D.
2. 已知向量，，则向量在向量方向上的投影向量为（ ）
A. B. C. D.
3. 已知，且不共面，若，则（ ）
A. B. C. 8D. 13
4. 用0，1，2，3，4，5这六个数字组成的无重复数字的四位偶数共有（ ）个
A. 150个B. 156个C. 144个D. 300个
5. 如图，四棱锥中，平面，底面为直角梯形，，，，点在棱上，且，则平面与平面的夹角的余弦值为
A. B. C. D.
6. 菱形的边长为4，，E为AB的中点（如图1），将沿直线DE翻折至处（如图2），连接，，若四棱锥的体积为，点F为的中点，则F到直线BC的距离为（ ）

A. B. C. D.
7. 小明在某一天中有七个课间休息时段，为准备“小歌手”比赛他想要选出至少一个课间休息时段来练习唱歌，但他希望任意两个练习时间段之间都有至少两个课间不唱歌让他休息，则小明一共有（ ）种练习的方案.
A. 31B. 18C. 21D. 33
8. 如图，正方体中，E是棱的中点，F是侧面上的动点，且平面，则与平面所成角的正切值t构成的集合是（ ）
A. B. C. D.
二、多选题：本题共3小题，共18分．在每小题给出的选项中，有多项符合题目要求．
9. 关于空间向量，以下说法正确是（ ）
A. 两个非零向量与任何一个向量都不能构成空间一个基底，则这两个向量共线
B. 已知向量，若，则钝角．
C. 若直线l的方向向量与平面的法向量的夹角等于，则直线l与平面α所成的角为
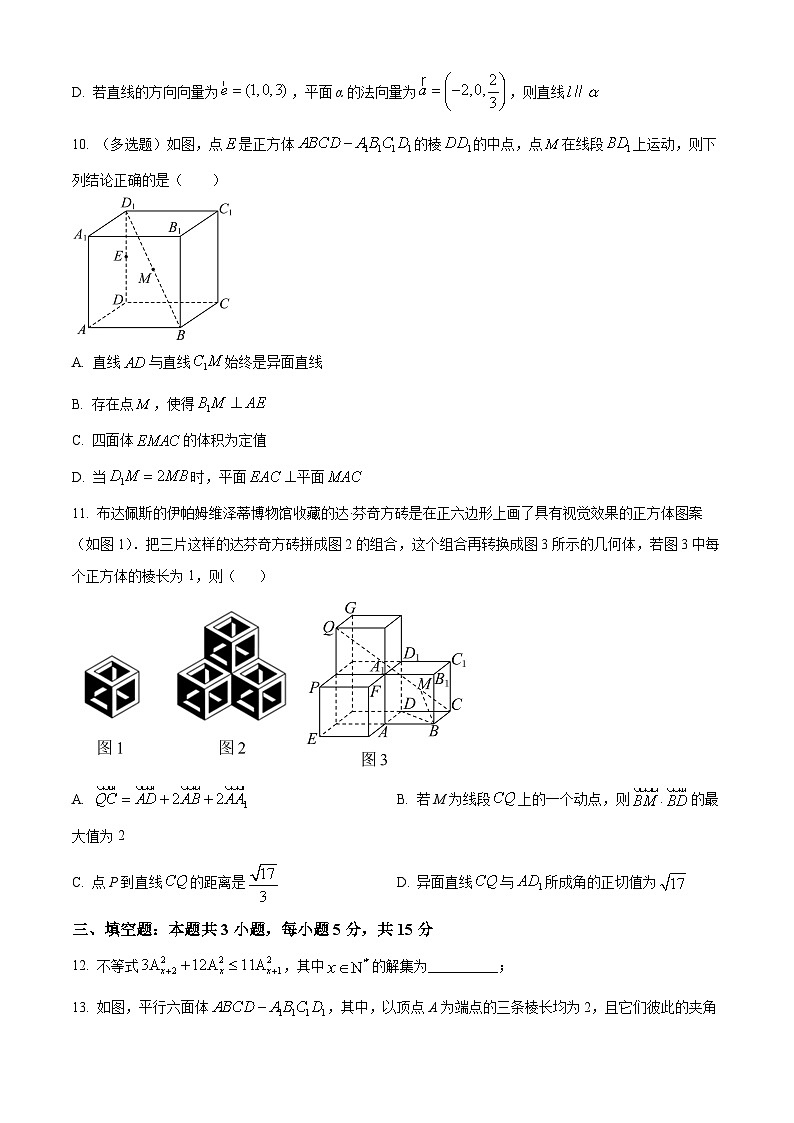
D. 若直线的方向向量为，平面α的法向量为，则直线
10. （多选题）如图，点是正方体棱的中点，点在线段上运动，则下列结论正确的是（ ）

A. 直线与直线始终是异面直线
B. 存在点，使得
C. 四面体的体积为定值
D. 当时，平面平面
11. 布达佩斯的伊帕姆维泽蒂博物馆收藏的达·芬奇方砖是在正六边形上画了具有视觉效果的正方体图案（如图1）．把三片这样的达芬奇方砖拼成图2的组合，这个组合再转换成图3所示的几何体，若图3中每个正方体的棱长为1，则（ ）

A. B. 若M为线段上的一个动点，则的最大值为2
C. 点P到直线的距离是D. 异面直线与所成角的正切值为
三、填空题：本题共3小题，每小题5分，共15分
12. 不等式，其中的解集为__________；
13. 如图，平行六面体，其中，以顶点A为端点的三条棱长均为2，且它们彼此的夹角都是，则异面直线与所成角的正切值为__________．
14. 现安排甲、乙、丙、丁、戊5名学生分别担任语文、数学、英语、物理、化学学科的科代表，要求甲不当语文科代表，乙不当数学科代表，若丙当物理科代表则丁必须当化学科代表，则不同的选法共有_____种
四、解答题：本题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤．
15. 已知空间中三点，，.
（1）若四边形ABCD是平行四边形，求点D坐标；
（2）若，且，求向量；
（3）若点在平面内，求的值.
16. 某班级周六的课程表要排入历史、语文、数学、物理、体育、英语共6节课．
（1）如果数学和语文必须排在一起，则有多少种不同的排法？
（2）语文必须排第一课，物理和数学不能排一起，则不同的排法有多少种？
（3）如果第一节不排体育，最后一节不排数学，那么共有多少种不同的排法？
（4）如果数学必须比语文先上，语文比英语先上（三课不一定连续上），则共有多少种不同的排法？
（5）原定的6节课已经排好，学校临时通知要增加生物、化学、地理3节课，若将这3节课插入原课表中且原来的6节课相对顺序不变，那么共有多少种不同的排法？
（答题要求：写上必要的文字说明，先列式，后计算）
17. 如图，在三棱锥中，平面平面，，，分别为､的中点，，.
（1）求点到直线的距离
（2）求平面与平面夹角的余弦值
（3）已知是平面内一点，点为中点，且平面，求线段的长.
18. 如图，在三棱柱中，，侧面是正方形，二面角的大小是．
（1）求到平面的距离．
（2）线段上是否存在一个点D，使直线与平面所成角为？若存在，求出的长；若不存在说明理由．
19. 如图，P为圆锥的顶点，O是圆锥底面的圆心，为底面直径，为底面圆O的内接正三角形，点E在母线上，且，.
（1）求证：平面平面；
（2）若点M为线段上的动点，当直线与平面所成角的正弦值最大时，求此时点到平面的距离.
江苏省靖江高级中学2023-2024学年第二学期阶段考试
高二数学试卷
一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的选项中，只有一项是符合题目要求的．
1. 如图，在三棱柱中，，分别是，的中点，，则（ ）
A. 1B. C. 0.5D.
【答案】B
【解析】
【分析】根据空间向量的基本定理求解即可.
【详解】如图，连接.
因为，分别是，的中点，
，
所以，，，
则.
故选：B.
2. 已知向量，，则向量在向量方向上的投影向量为（ ）
A B. C. D.
【答案】D
【解析】
【分析】根据投影向量的定义求解即可.
【详解】依题意，向量在向量方向上的投影向量为：，
故选：D
3. 已知，且不共面，若，则（ ）
A. B. C. 8D. 13
【答案】B
【解析】
【分析】根据共线定理和空间向量基本定理求解即可.
【详解】因为，
所以，
又不共面，
所以，解得，
所以.
故选：B
4. 用0，1，2，3，4，5这六个数字组成的无重复数字的四位偶数共有（ ）个
A. 150个B. 156个C. 144个D. 300个
【答案】B
【解析】
【分析】当末位是数字0时，可以组成个数字；当末位不是0时，共有种结果，根据计数原理得到结果.
【详解】本题需要分两类来解，
当末位是数字0时，可以组成个四位偶数，
当末位不是0时，末位可以是2、4，有两种选法，
首位有4种选法，中间两位可以从余下的4个数字中选两个，共有种结果，
根据分类计数原理知共有种结果.
故选：B.
5. 如图，四棱锥中，平面，底面为直角梯形，，，，点在棱上，且，则平面与平面的夹角的余弦值为
A. B. C. D.
【答案】B
【解析】
【详解】
以B为坐标原点,分别以BC、BA、BP所在直线为x、y、z轴,
建立空间直角坐标系，
则，
∴
设平面BED的一个法向量为，
则，
取z=1,得，
平面ABE的法向量为，
∴.
∴平面ABE与平面BED的夹角的余弦值为.
故选B.
点睛：用向量法求二面角大小的两种方法：
（1）分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量，则这两个向量的夹角的大小即为二面角的大小；
（2）分别求出二面角的两个半平面的法向量，然后通过两个法向量的夹角得到二面角大小，解题时要注意结合图形判断出所求的二面角是锐角还是钝角.
6. 菱形的边长为4，，E为AB的中点（如图1），将沿直线DE翻折至处（如图2），连接，，若四棱锥的体积为，点F为的中点，则F到直线BC的距离为（ ）

A. B. C. D.
【答案】A
【解析】
【分析】由已知可证得 平面，平面，所以以为原点，所在的直线分别为轴，建立空间直角坐标系，利用空间向量求解即可.
【详解】连接，因为四边形为菱形，且，所以为等边三角形，
因为 E为AB的中点，所以，所以，
因为，平面，所以 平面，
因为菱形的边长为4，所以，
所以直角梯形的面积为，
设四棱锥的高为，则，得，
所以，所以平面，
所以以为原点，所在的直线分别为轴，建立空间直角坐标系，则
，
所以，
所以
所以，
所以F到直线BC的距离为，
故选：A

7. 小明在某一天中有七个课间休息时段，为准备“小歌手”比赛他想要选出至少一个课间休息时段来练习唱歌，但他希望任意两个练习的时间段之间都有至少两个课间不唱歌让他休息，则小明一共有（ ）种练习的方案.
A. 31B. 18C. 21D. 33
【答案】B
【解析】
【分析】根据练习唱歌的课间个数进行分类讨论，利用列举法来求得正确答案.
【详解】七个课间编号为，
如果仅有一个课间练习，则每个课间都可以，有7种方案，
若有两个课间练习，选法有，
共种方案，
三个课间练习，选法为，共种，
故总数为种.
故选：B
8. 如图，正方体中，E是棱的中点，F是侧面上的动点，且平面，则与平面所成角的正切值t构成的集合是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】记的中点分别为，先证平面平面，从而可知点F在线段GH上，然后作出所求角即可求解.
【详解】记的中点分别为，连接，
设，由正方体性质可知，，
又分别为的中点，所以，所以，
又平面，平面，所以平面，
由正方体性质知，，且，
所以四边形为平行四边形，则，
又平面，平面，所以平面，
因为，平面，
所以平面平面，
因为平面，所以点F在线段GH上，
由正方体性质可知，平面，
所以即为与平面所成角，，
易知，当F为的中点时，取得最小值，
当F与（或）重合时，取得最大值，即，
所以.
故选：D
二、多选题：本题共3小题，共18分．在每小题给出的选项中，有多项符合题目要求．
9. 关于空间向量，以下说法正确的是（ ）
A. 两个非零向量与任何一个向量都不能构成空间的一个基底，则这两个向量共线
B. 已知向量，若，则为钝角．
C. 若直线l的方向向量与平面的法向量的夹角等于，则直线l与平面α所成的角为
D. 若直线的方向向量为，平面α的法向量为，则直线
【答案】AC
【解析】
【分析】A. 由空间向量基底的判断；B.由时，向量共线且反向判断；C.由l与平面α所成的角为判断；D.由和直线与平面的位置关系判断.
【详解】A. 由空间向量基底的概念知：两个非零向量与任何一个向量都不能构成空间的一个基底，则这两个向量共线，故A正确；
B.当时，向量共线且反向，但不是钝角．故B错误；
C.由题意直线l与平面α所成的角为，故C正确；
D.直线的方向向量为，平面α的法向量为，且，则直线或，故D错误；
故选：AC
10. （多选题）如图，点是正方体的棱的中点，点在线段上运动，则下列结论正确的是（ ）

A. 直线与直线始终是异面直线
B. 存在点，使得
C. 四面体的体积为定值
D. 当时，平面平面
【答案】BCD
【解析】
【分析】对于A选项，当位于中点时，与共面；对于选项B和D可采用空间向量计算，对于C选项，连接,交于 ，此时//，易证所以四面体的体积为定值.
【详解】解：

对于A选项，连接交与，当点在点时，直线与直线相交，故A选项不正确；
对于C.选项，连接,交于 ，此时//，故线段到平面的距离为定值，所以四面体的体积为定值，故C选项正确；
以为坐标原点，建立如图的坐标系，设正方体的边长为，则，，，， ，，
对于B选项， 存在点，使得，
则， ，，所以，得，故当满足时，，
故B选项正确；
对于D选项，当满足时，，
， ，故平面的法向量可求得为：，
，，故平面的法向量可求得为：，
所以，即平面平面，故D选项.
故选：BCD.
【点睛】本题考查空间直线与直线的位置关系判断，考查空间平面与平面的位置关系判断，以及几何体的体积计算等，难度一般.
11. 布达佩斯的伊帕姆维泽蒂博物馆收藏的达·芬奇方砖是在正六边形上画了具有视觉效果的正方体图案（如图1）．把三片这样的达芬奇方砖拼成图2的组合，这个组合再转换成图3所示的几何体，若图3中每个正方体的棱长为1，则（ ）

A. B. 若M为线段上的一个动点，则的最大值为2
C. 点P到直线的距离是D. 异面直线与所成角的正切值为
【答案】BCD
【解析】
【分析】建立空间直角坐标系，根据坐标运算可判断A；利用坐标表示出，即可判断B；根据点到直线的向量公式可判断C；利用向量夹角公式和同角三角函数的基本关系求解，可判断D.
【详解】如图建立空间直角坐标系，
则，
故，
，
所以，A错误；
记，则，
所以，
当时，取得最大值2，B正确；
记同向的单位向量为，
则点P到直线的距离，C正确；
记异面直线与所成角为，
则，
所以，所以，D正确.
故选：BCD

三、填空题：本题共3小题，每小题5分，共15分
12. 不等式，其中的解集为__________；
【答案】
【解析】
【分析】根据排列数公式化简，即可求解.
【详解】由题知，，且，
又，
即，
解得，故或，
所以，原不等式的解集为.
故答案为：
13. 如图，平行六面体，其中，以顶点A为端点的三条棱长均为2，且它们彼此的夹角都是，则异面直线与所成角的正切值为__________．
【答案】
【解析】
【分析】记，以为基底表示出，然后利用数量积性质求出，由夹角公式求出，然后可得.
【详解】记，
则，，
因为，
所以，
，
，
记异面直线与所成角为，
则，
所以，所以.
故答案为：
14. 现安排甲、乙、丙、丁、戊5名学生分别担任语文、数学、英语、物理、化学学科的科代表，要求甲不当语文科代表，乙不当数学科代表，若丙当物理科代表则丁必须当化学科代表，则不同的选法共有_____种
【答案】67
【解析】
【分析】根据特殊元素特殊处理的原则，以丙进行分类，排完丙后，由甲不当语文科代表，乙不当数学科代表，还要进行分类，根据分类计数原理可得.
【详解】因为丙当物理课代表则丁必须当化学课代表，以丙进行分类：
第一类，当丙当物理课代表时，丁必须当化学课代表，再根据甲当数学课代表，乙戊可以当英语和语文中的任一课，有种，当甲不当数学课代表，甲只能当英语课代表，乙只能当语文课代表，戊当数学课代表，有种，
共计种；
第二类，当丙不当物理课代表时，分四类：
①丙为语文课代表时，乙只能从英语、物理和化学中选择一课，剩下的甲丁戊任意排给剩下的三课，有种种，
②丙为数学课代表时，甲只能从英语、物理和化学中选择一课，剩下的乙丁戊任意排给剩下的三课，有种，
③丙为英语课代表时，继续分类，甲当数学课代表时，其他三位同学任意当有种，当甲不当数学课代表，甲只能从物理和化学课中选一课,乙只能从语文和甲选完后的剰下的一课中选一课，丁和戊做剰下的两课，有种，共计种，
④丙为化学课代表时，同③的选法一样有种，
根据分类计数原理得，不同的选法共有种.
故答案为：67.
四、解答题：本题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤．
15. 已知空间中三点，，.
（1）若四边形ABCD是平行四边形，求点D坐标；
（2）若，且，求向量；
（3）若点在平面内，求的值.
【答案】（1）
（2）或
（3）
【解析】
【分析】（1）根据平行四边形的性质得到，再代入坐标，即可求解；
（2）根据向量平行的定理可知，，再代入向量模的公式，即可求解；
（3）利用空间向量共面可知，，再代入坐标运算，即可求解.
【小问1详解】
设点，
由题意可知，，所以，
得，
所以点的坐标为；
【小问2详解】
，因为，
所以，
因为，所以，得，
所以向量或；
【小问3详解】
因为点在平面上，故存在实数使得，
又，,
所以，解得.
故.
16. 某班级周六的课程表要排入历史、语文、数学、物理、体育、英语共6节课．
（1）如果数学和语文必须排在一起，则有多少种不同的排法？
（2）语文必须排第一课，物理和数学不能排一起，则不同的排法有多少种？
（3）如果第一节不排体育，最后一节不排数学，那么共有多少种不同的排法？
（4）如果数学必须比语文先上，语文比英语先上（三课不一定连续上），则共有多少种不同的排法？
（5）原定的6节课已经排好，学校临时通知要增加生物、化学、地理3节课，若将这3节课插入原课表中且原来的6节课相对顺序不变，那么共有多少种不同的排法？
（答题要求：写上必要的文字说明，先列式，后计算）
【答案】16. 240；
17 72； 18. 484；
19. 120； 20. 504.
【解析】
【分析】（1）利用捆绑法可解；
（2）利用插空法可解；
（3）对数学是否排在第一节分类讨论即可；
（4）定序问题利用除法可得；
（5）分步将3科插入空位可解.
小问1详解】
第一步，先将数学和语文排在一起，有种排法；
第二步，将数学和语文看成一个整体，与历史、物理、体育、英语一起全排，有种排法，
所以，数学和语文必须排在一起共有种排法.
【小问2详解】
第一步，先排语文，有1种排法；
第二步，将历史、体育、英语排成一排，有种排法；
第三步，在第二步产生的4个空位中插入物理和数学，有种排法.
所以，总的排法有种排法.
【小问3详解】
第一类，第一节排数学，其余五节任意排，有种排法；
第二类，第1步，从历史、语文、物理、英语中选一科排在第一节，有4种排法，
第2步，再从剩下的4个学科（不包括数学）中选一科排在最后一节，有4种排法，
第3步，中间4节任意排，有种排法，
所以，总排法有.
综上，满足条件的排法有种.
【小问4详解】
数学、语文、英语的上课顺序共有种，满足条件的顺序只有1种，
故满足条件的排法有种.
【小问5详解】
第一步，先在7个空位中选择一个空位排生物，有7种；
第二步，在排入生物之后产生的8个空位选择一个空位排化学，有8种；
第三步，在排入化学之后产生的9个空位选择一个空位排地理，有9种.
所以，总的排法有种.
17. 如图，在三棱锥中，平面平面，，，分别为､的中点，，.
（1）求点到直线的距离
（2）求平面与平面夹角的余弦值
（3）已知是平面内一点，点为中点，且平面，求线段的长.
【答案】（1）；
（2）；
（3）.
【解析】
【分析】（1）通过题中关系可推出△为等边三角形，进而可得解；
（2）通过证明，，可得即为所求，进而可得解；
（3）建立空间直角坐标系，设，利用可得坐标，进而得距离.
【小问1详解】
（1）,为中点，所以，
平面平面，平面平面，所以平面，
因为，所以，
，所以,
连接，则，所以，
所以△为等边三角形，所以点到直线的距离为；
【小问2详解】
平面平面，，平面平面，
所以平面，所以
易知，满足，所以，
又，平面，所以平面，
平面，所以.
所以即为平面与平面夹角，
，所以；
【小问3详解】
如图建立空间直角坐标系，是平面内一点，设，
，点为中点，，
，，
由平面，可得，
解得.所以，.
所以
18. 如图，在三棱柱中，，侧面是正方形，二面角的大小是．
（1）求到平面的距离．
（2）线段上是否存在一个点D，使直线与平面所成角为？若存在，求出的长；若不存在说明理由．
【答案】（1）；
（2）存在，
【解析】
【分析】（1）记的中点分别为，作于点，先证平面平面，然后计算可得；
（2）以的方向分别为x，y轴的正方向，过点F作垂直于平面的直线为z轴，建立空间直角坐标系，利用向量法求解即可.
【小问1详解】
记的中点分别为，
由是正方形可知，
又，所以，
因为二面角的大小是，所以，
由三棱柱性质可知，，所以四边形为平行四边形，
所以，
因为平面，所以平面，
又平面，所以平面平面，
作于点，
因为，平面平面，平面，
所以平面，所以即为所求，
所以.
【小问2详解】
以的方向分别为x，y轴的正方向，过点F作垂直于平面的直线为z轴，建立空间直角坐标系，
易知，，
则，
则，
设，
则，
设为平面的法向量，
则，取，得，
记直线与平面所成角为，
则
，
当，即时，取得最小值4，
故，
所以，当时，直线与平面所成角为.
此时，
所以.
19. 如图，P为圆锥的顶点，O是圆锥底面的圆心，为底面直径，为底面圆O的内接正三角形，点E在母线上，且，.
（1）求证：平面平面；
（2）若点M为线段上的动点，当直线与平面所成角的正弦值最大时，求此时点到平面的距离.
【答案】（1）证明见解析
（2）.
【解析】
【分析】（1）利用余弦定理与勾股定理推得，再利用线面垂直与面面垂直的判定定理与性质定理即可得证；
（2）建立空间直角坐标系，利用线面角向量表示得到关于的表达式，从而求得的值，进而利用点面距离公式即可得解.
【小问1详解】
如图，设交于点，连接，由圆锥的性质可知底面，

因为平面，所以，
又因为是底面圆的内接正三角形，由，可得，，
解得，又，，
所以，即，，
所以在中，，
在中，由余弦定理：
，
所以，故.
因为底面，面，所以平面平面，
又面，面面，，故面，
又平面，所以平面平面；
【小问2详解】
易知，以点为坐标原点，，，所在直线分别为x轴，y轴，z轴，建立如图所示的空间直角坐标系，

则，，，，，，
所以，，，，
设平面的法向量为，则，
令，则，
设，可得，
设直线与平面所成的角为，则，
即，
令，，
则
当且仅当，即时，等号成立，
所以当时，有最大值4，
即当时，的最大值为1，此时点，
所以，
所以点M到平面的距离，
故当直线与平面所成角的正弦值最大时，点到平面的距离为.