
2024年新高考数学一轮复习达标检测第54讲分类加法计数原理与分步乘法计数原理(学生版)
展开1.高二年级要从3名男生,2名女生中选派3人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案有( )
A.6种B.7种C.8种D.9种
2.今有6个人组成的旅游团,包括4个大人,2个小孩,去庐山旅游,准备同时乘缆车观光,现有三辆不同的缆车可供选择,每辆缆车最多可乘3人,为了安全起见,小孩乘缆车必须要大人陪同,则不同的乘车方式有( )种
A.204B.288C.348D.396
3.某校教学大楼共有五层,每层均有两个楼梯,一学生由一层到五层的走法有( )
A.10种B.25种C.52种D.24种
4.从集合{0,1,2,3,4,5,6}中任取两个互不相等的数a,b,组成复数a+bi,其中虚数有( )
A.36个B.42个C.30个D.35个
5.如图,湖面上有4个相邻的小岛A,B,C,D,现要建3座桥梁,将这4个小岛连接起来共有m种不同的方案,则m的值为( )
A.4B.8C.12D.16
6.学校计划在周一至周四的艺术节上展演《雷雨》、《茶馆》、《天籁》、《马蹄声碎》四部话剧,每天一部,受多种因素影响,话剧《雷雨》不能在周一、周四上演;《茶馆》不能在周一、周三上演;《天籁》不能在周三、周四上演;《马蹄声碎》不能在周一、周四上演,则所有的可能情况有( )种.
A.0B.1C.2D.3
7.电路如图所示,在A,B间有四个开关,若发现A,B之间电路不通,则这四个开关打开或闭合的方式有( )
A.3种B.8种C.13种D.16种
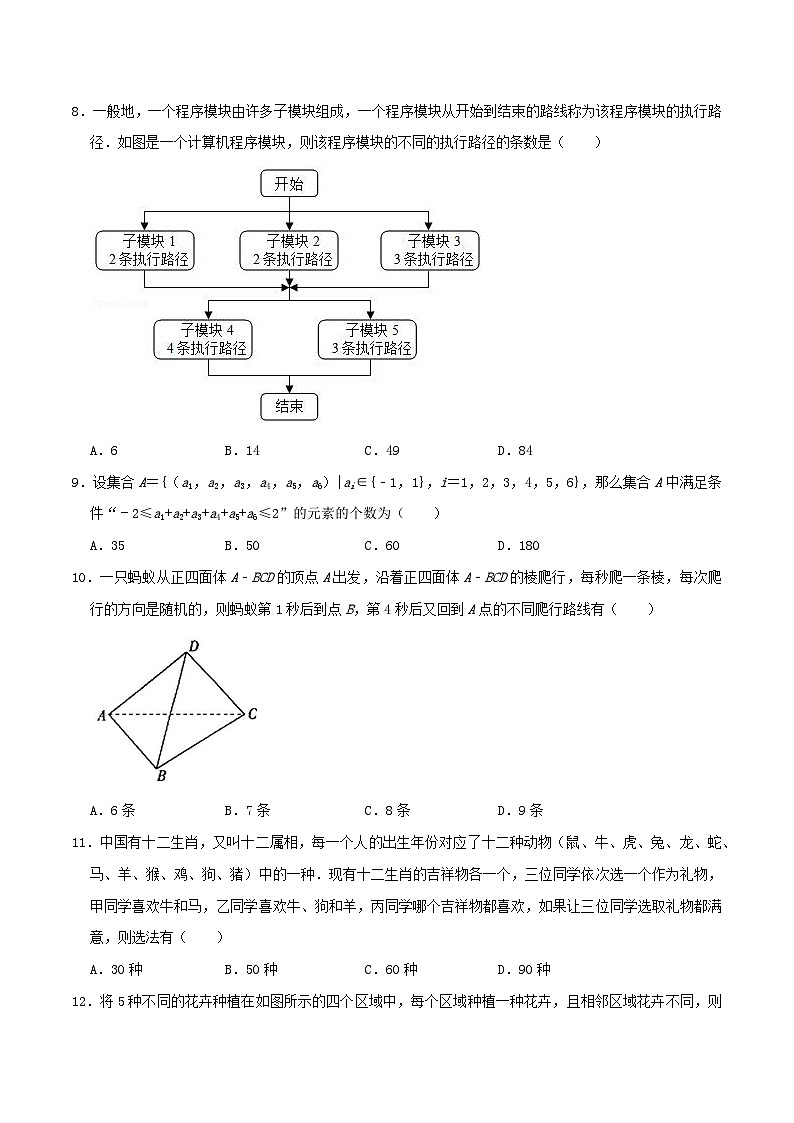
8.一般地,一个程序模块由许多子模块组成,一个程序模块从开始到结束的路线称为该程序模块的执行路径.如图是一个计算机程序模块,则该程序模块的不同的执行路径的条数是( )
A.6B.14C.49D.84
9.设集合A={(a1,a2,a3,a4,a5,a6)|ai∈{﹣1,1},i=1,2,3,4,5,6},那么集合A中满足条件“﹣2≤a1+a2+a3+a4+a5+a6≤2”的元素的个数为( )
A.35B.50C.60D.180
10.一只蚂蚁从正四面体A﹣BCD的顶点A出发,沿着正四面体A﹣BCD的棱爬行,每秒爬一条棱,每次爬行的方向是随机的,则蚂蚁第1秒后到点B,第4秒后又回到A点的不同爬行路线有( )
A.6条B.7条C.8条D.9条
11.中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种.现有十二生肖的吉祥物各一个,三位同学依次选一个作为礼物,甲同学喜欢牛和马,乙同学喜欢牛、狗和羊,丙同学哪个吉祥物都喜欢,如果让三位同学选取礼物都满意,则选法有( )
A.30种B.50种C.60种D.90种
12.将5种不同的花卉种植在如图所示的四个区域中,每个区域种植一种花卉,且相邻区域花卉不同,则不同的种植方法种数是( )
A.420B.180C.64D.25
13.假如某人有壹元、贰元、伍元、拾元、贰拾元、伍拾元、壹佰元的纸币各两张,要支付贰佰壹拾玖(219)元的货款(不找零),则有 种不同的支付方式.
14. 2019年女排世界杯共有12支参赛球队,赛制采用12支队伍单循环,两两捉对厮杀一场定胜负,依次进行,则此次杯赛共有 场球赛.
15.4位学生和1位老师站成一排照相,若老师站中间,男生甲不站最左端,男生乙不站最右端,则不同排法的种数是 .
16.若A∪B={1,2,3},则集合A,B共有 种组合.
17.现用五种不同的颜色,要对如图中的四个部分进行着色,要求公共边的两块不能用同一种颜色,共有 种不同着色方法
18.如图所示,玩具计数算盘的三档上各有7个算珠,现将每档算珠分为左右两部分,左侧的每个算珠表示数2,右侧的每个算珠表示数1(允许一侧无珠),记上、中、下三档的数字和分别为a,b,c.例如,图中上档的数字和a=9.若a,b,c成等差数列,则不同的分珠计数法有 种.
19.我国古代数学著作《孙子算经》中记载:“今有三人共车,二车空,二人共车,九人步.问人车各几何?”其大意是:“每车坐3人,两车空出来;每车坐2人,多出9人步行.问人数和车数各多少?”根据题意,其车数为 辆.
20.北京大兴国际机场为4F级国际机场、大型国际枢纽机场、国家发展新动力源,于2019年9月25日正式通航.目前建有“三纵一横”4条跑道,分别叫西一跑道、西二跑道、东一跑道、北一跑道,如图所示;若有2架飞往不同目的地的飞机要从以上不同跑道同时起飞,且西一跑道、西二跑道至少有一道被选取,则共有 种不同的安排方法.(用数字作答).
21.从分别印有数字0,3,5,7,9的5张卡片中,任意抽出3张组成三位数.
①求可以组成多少个大于500的三位数;
②求可以组成多少个三位数;
③若印有9的卡片,既可以当9用,也可以当6用,求可以组成多少个三位数.
[B组]—强基必备
1.如图,用四种不同的颜色给图中的A,B,C,D,E,F,G七个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法有( )
A.192B.336
C.600D.以上答案均不对
2.设S为一个非空有限集合,记|S|为集合S中元素的个数,若集合S的两个子集A、B满足:|A∩B|=k并且A∪B=S,则称子集{A,B}为集合S的一个“k﹣覆盖”(其中0≤k≤|S|),若|S|=n,则S的“k﹣覆盖”个数为 .
2024年新高考数学一轮复习知识梳理与题型归纳第55讲分类加法计数原理与分步乘法计数原理(学生版): 这是一份2024年新高考数学一轮复习知识梳理与题型归纳第55讲分类加法计数原理与分步乘法计数原理(学生版),共4页。试卷主要包含了分类加法计数原理,分步乘法计数原理等内容,欢迎下载使用。
2024年新高考数学一轮复习题型归纳与达标检测第55讲分类加法计数原理与分步乘法计数原理(讲)(Word版附解析): 这是一份2024年新高考数学一轮复习题型归纳与达标检测第55讲分类加法计数原理与分步乘法计数原理(讲)(Word版附解析),共6页。试卷主要包含了分类加法计数原理,分步乘法计数原理等内容,欢迎下载使用。
高中数学高考第55讲 分类加法计数原理与分步乘法计数原理(讲)(学生版): 这是一份高中数学高考第55讲 分类加法计数原理与分步乘法计数原理(讲)(学生版),共5页。试卷主要包含了分类加法计数原理,分步乘法计数原理等内容,欢迎下载使用。












