
2024年新高考数学一轮复习达标检测第22讲函数y=Asinωx+φ的图象及应用(学生版)
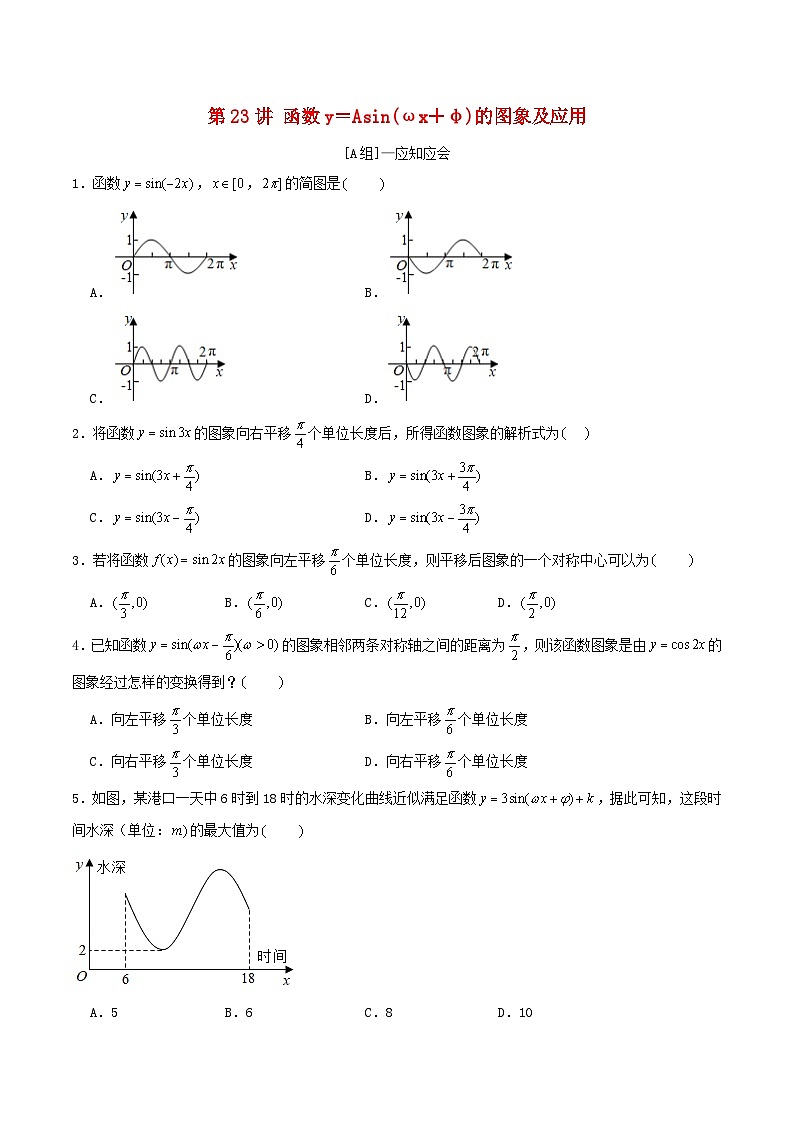
展开1.函数,,的简图是
A.B.
C.D.
2.将函数的图象向右平移个单位长度后,所得函数图象的解析式为
A.B.
C.D.
3.若将函数的图象向左平移个单位长度,则平移后图象的一个对称中心可以为
A.B.C.D.
4.已知函数的图象相邻两条对称轴之间的距离为,则该函数图象是由的图象经过怎样的变换得到?
A.向左平移个单位长度B.向左平移个单位长度
C.向右平移个单位长度D.向右平移个单位长度
5.如图,某港口一天中6时到18时的水深变化曲线近似满足函数,据此可知,这段时间水深(单位:的最大值为
A.5B.6C.8D.10
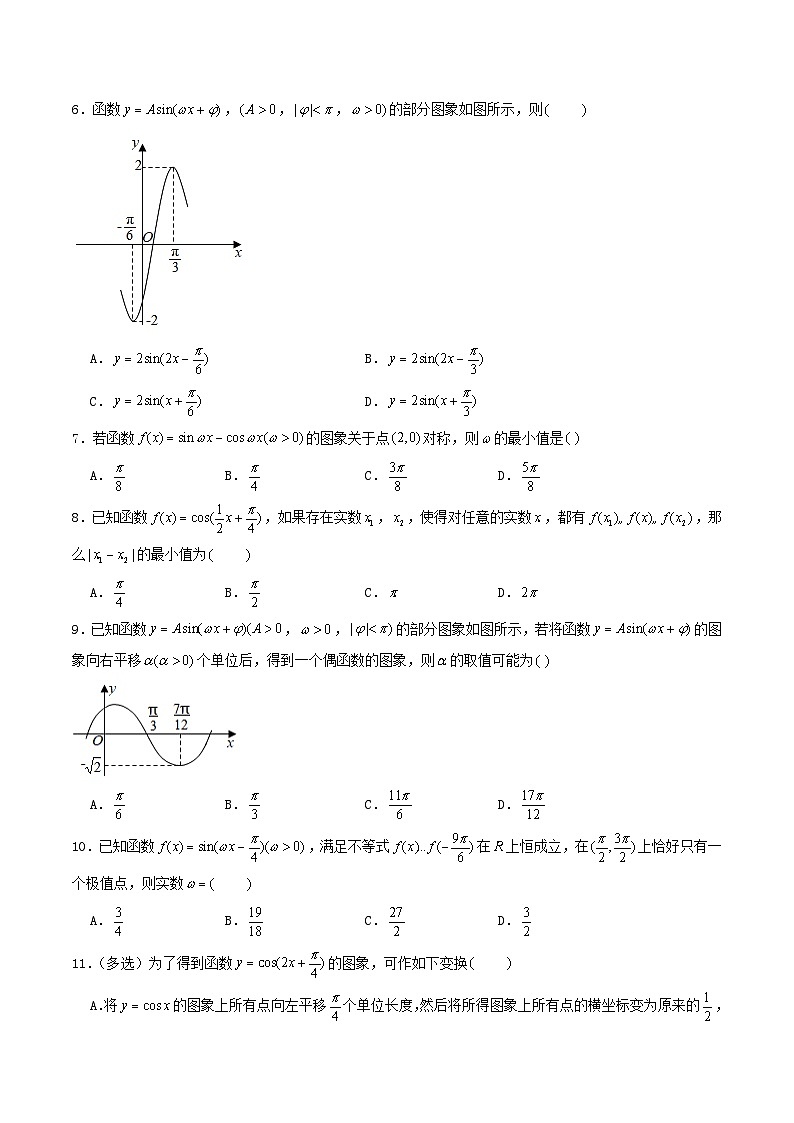
6.函数,,,的部分图象如图所示,则
A.B.
C.D.
7.若函数的图象关于点对称,则的最小值是
A.B.C.D.
8.已知函数,如果存在实数,,使得对任意的实数,都有,那么的最小值为
A.B.C.D.
9.已知函数,,的部分图象如图所示,若将函数的图象向右平移个单位后,得到一个偶函数的图象,则的取值可能为
A.B.C.D.
10.已知函数,满足不等式在上恒成立,在上恰好只有一个极值点,则实数
A.B.C.D.
11.(多选)为了得到函数的图象,可作如下变换
A.将的图象上所有点向左平移个单位长度,然后将所得图象上所有点的横坐标变为原来的,纵坐标不变而得到
B.将的图象上所有点向右平移个单位长度,然后将所得图象上所有点的横坐变为原来的2倍,纵坐标不变而得到
C.将的图象上所有点的横坐标变为原来的,纵坐标不变,然后将所得图象上所有点向左平移个单位长度而得到
D.将的图象上所有点的横坐标变为原来的,纵坐标不变,然后将所得图象上所有点向左平移个单位长度而得到
12.(多选)已知函数,,的图象的一个最高点为,,与之相邻的一个对称中心为,将的图象向右平移个单位长度得到函数的图象,则
A.为偶函数
B.的一个单调递增区间为
C.为奇函数
D.在上只有一个零点
13.函数的最小值为 .
14.若函数的最小正周期为,将的图象向左平移个单位后,所得图象关于轴对称,则的最小正值为 .
15.把函数的图象向右平移个单位,得函数的图象,则的值等于 .
16.已知函数的图象如图所示,则 .
17.函数图象上有两点,,,若对任意,线段与函数图象都有五个不同交点,若在,和,上单调递增,在,上单调递减,且,则的所有可能值是
18.已知函数.
(1)求函数的对称轴方程;
(2)求函数在区间上的最大值和最小值.
19.已知函数的最小正周期为.
(1)从,都有这三个条件中,选择合适的两个条件,求函数的解析式;
(2)求(1)中所求得的函数在区间上的最大值和最小值.
20.将函数的图象向右平移个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的2倍后所得到的图象对应的函数记作.
(1)在中,三个内角,,且,若角满足(C),求的取值范围;
(2)已知常数,,且函数在内恰有2021个零点,求常数与的值.
[B组]—强基必备
1.将函数的图象向右平移个单位长度,再将横坐标缩短为原来的得到函数的图象,若在,上的最大值为,则的取值个数为
A.1B.2C.3D.4
2.函数在区间上的最大值与最小值之差的取值范围是
A.B.,C.,D.,
3.已知函数,函数的图象经过点且的最小正周期为.
(1)求函数的解析式;
(2)将函数图象上所有的点向下平移1个单位长度,再桦函数图象上所有点的横坐标变为原来的2倍,纵坐标不变,再将图象上所有的点的横坐标不变,纵坐标变为原来的倍,得到函数图象,令函数,区间,,且满足:在,上至少有30个零点,在所有满足上述条件的,中,求的最小值.
(3)若对任意,恒成立,求实数的取值范围.
2024年新高考数学一轮复习达标检测第22讲函数y=Asinωx+φ的图象及应用(教师版): 这是一份2024年新高考数学一轮复习达标检测第22讲函数y=Asinωx+φ的图象及应用(教师版),共16页。
2024年新高考数学一轮复习知识梳理与题型归纳第23讲函数y=Asinωx+φ的图象及应用(学生版): 这是一份2024年新高考数学一轮复习知识梳理与题型归纳第23讲函数y=Asinωx+φ的图象及应用(学生版),共8页。试卷主要包含了函数y=Asin的有关概念等内容,欢迎下载使用。
高考数学一轮复习 专题5.5 函数y=Asin(ωx+φ)的图象及其应用(讲): 这是一份高考数学一轮复习 专题5.5 函数y=Asin(ωx+φ)的图象及其应用(讲),文件包含专题55函数y=Asinωx+φ的图象及其应用讲教师版docx、专题55函数y=Asinωx+φ的图象及其应用讲学生版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。












