数学6.7 点到直线的距离公式教学设计

这是一份数学6.7 点到直线的距离公式教学设计，共4页。教案主要包含了课前知识储备，学生知识储备检测，发布任务，小组讨论，完成任务，对照练习，随堂练习，课堂检测等内容，欢迎下载使用。
1.已知点A(-4,0)和B(2,6)，则点A和点B的距离为 .
2.直线x+y-4=0与直线4x-3y+5=0的交点坐标为 .
3.经过点M(1,-3)且与直线3x-y+7=0垂直的直线的方程为 .
附录2：学生知识目标检测
1.点P(2,-1)到直线3x-4y+5=0的距离为 .
2.已知点(m,0)到直线x+y-3=0的距离为2，则m的值为 .
3.两条平行直线3x-4y+2=0与3x-4y-13=0之间的距离为 .授课题目
6.7点到直线的距离公式
授课类型
新授课
建议学时
1学时
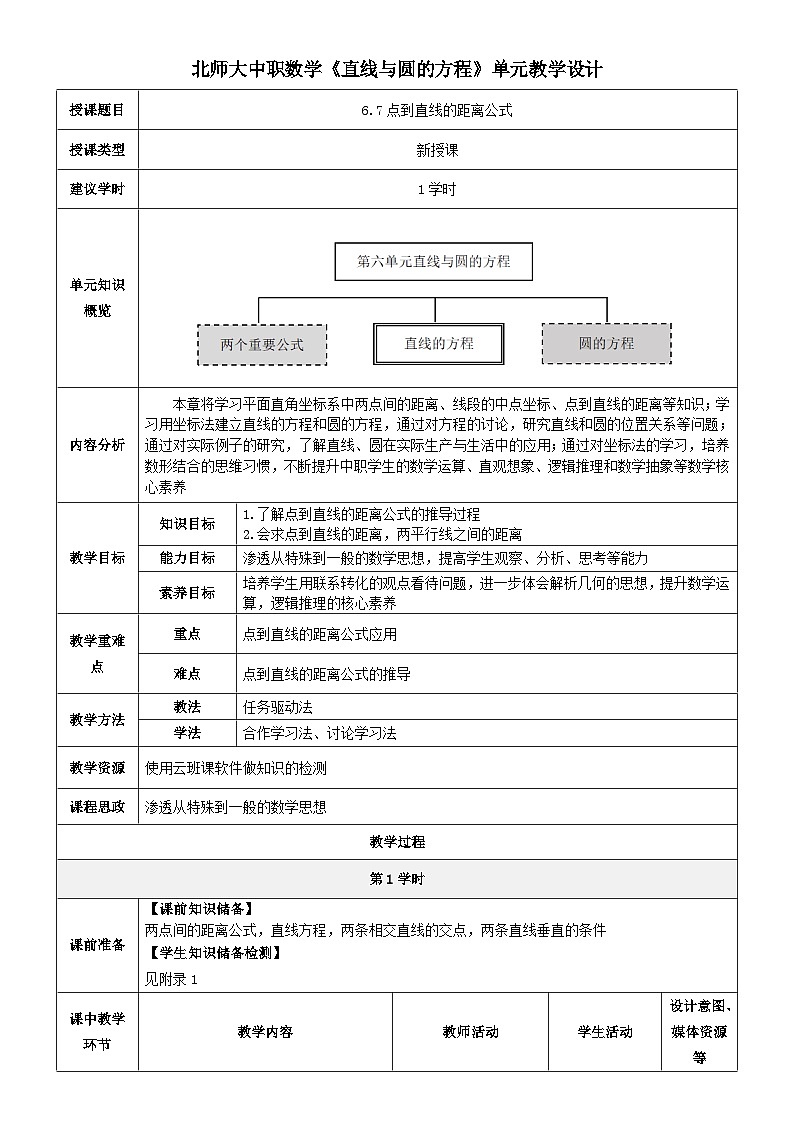
单元知识概览
内容分析
本章将学习平面直角坐标系中两点间的距离、线段的中点坐标、点到直线的距离等知识；学习用坐标法建立直线的方程和圆的方程，通过对方程的讨论，研究直线和圆的位置关系等问题；通过对实际例子的研究，了解直线、圆在实际生产与生活中的应用；通过对坐标法的学习，培养数形结合的思维习惯，不断提升中职学生的数学运算、直观想象、逻辑推理和数学抽象等数学核心素养
教学目标
知识目标
1.了解点到直线的距离公式的推导过程
2.会求点到直线的距离，两平行线之间的距离
能力目标
渗透从特殊到一般的数学思想，提高学生观察、分析、思考等能力
素养目标
培养学生用联系转化的观点看待问题，进一步体会解析几何的思想，提升数学运算，逻辑推理的核心素养
教学重难点
重点
点到直线的距离公式应用
难点
点到直线的距离公式的推导
教学方法
教法
任务驱动法
学法
合作学习法、讨论学习法
教学资源
使用云班课软件做知识的检测
课程思政
渗透从特殊到一般的数学思想
教学过程
第1学时
课前准备
【课前知识储备】
两点间的距离公式，直线方程，两条相交直线的交点，两条直线垂直的条件
【学生知识储备检测】
见附录1
课中教学环节
教学内容
教师活动
学生活动
设计意图、媒体资源等
（一）
情景导入
图6-27
在平面直角坐标系中，点P(4,4)不在直线l：x+y−2=0上，过点P作直线l的垂线，垂足为Q，如图6-27.则线段PQ的长称为点P到直线l的距离.那么，这个距离怎样求呢？
【发布任务】
全班分小组，明确小组长的任务
【小组讨论】
1.分组讨论，由组长记录
2.每个小组长归纳总结并展示
从具体问题入手，由易到难，符合学生认知发展水平
（二）
合作探究
由已知可求得线段PQ所在的直线的方程为x−y=0.
解方程组x+y−2=0，x−y=0， 可得垂足Q的坐标为(1,1).
所以根据两点间距离公式，点P到直线l的距离
PQ=4−12+4−12=32. 合作交流：
观察图6-27，你能否在不求出垂足Q的坐标的情况下，计算出点P到直线l的距离？
提示：可过点P分别作x轴、y轴的垂线交直线l于点A，B，利用直角三角形的面积公式可得S△PAB=12PA∙PB=12AB∙d（其中d为点P到直线l的距离），可求出d，你能试一试吗？
引导学生将点到直线的距离转化为两点间的距离
【发布任务】
提示学生其他思路并由小组合作完成
利用旧知求解
【完成任务】
各小组学生利用三角形的面积公式来求点到直线的距离
1.为探究点到直线距离公式提供思路
2.一题多解，提升学生数学思维能力
（三）
抽象概括
在平面直角坐标系中，已知点P(x0,y0)和直线l：Ax+By+C=0，则点P到直线l的距离d可以通过“分析理解”中的方法推导和计算得到：
d=Ax0+By0+CA2+B2.
上述公式叫作点到直线的距离公式.比如，“问题提出”中的距离可直接计算d=4+4−212+12=62=32.
强调直线的方程必须要转化成一般式
告诉学生记忆方式
抓住关键字词，并做好笔记
1.培养学生的数学抽象核心素养
2.渗透类比的数学思想
3.为后续学直线与圆位置关系做准备
（四）
示范讲解
例1 求点P(−1,2)到直线l：2x+y−5=0的距离.
分析 本题是对点到直线的距离公式的直接应用，只需判断公式中x0，y0，A，B，C的值，代入公式计算即可.
解x0=−1，y0=2，A=2，B=1，C=−5代入点到直线的距离公式中，得d=2×(−1)+2−522+12=5.
例2 求点P(−2,3)到直线l：x=4的距离.
分析 本题是对点到直线的距离公式的直接应用，需要先将直线的方程转化为一般式方程，明确公式中x0，y0，A，B，C的值，再代入公式计算即可.
解 依题意可得x0=−2，y0=3，将直线l的方程转化为一般式方程x−4=0，可得A=1，B=0，C=−4，代入点到直线的距离公式中，得d=1×(−2)+0×3−412+02=6.
例3 已知点Pa,−1到直线x+
2y−8=0的距离等于5，求a的值.
解 根据点到直线的距离公式得d=a+2×−1−812+22=5，化简得a−10
=5，所以a−10=5或a−10=−5，即a=15或a=5.
例4 求平行直线l1：3x−4y−12=0和l2：3x−4y+6=0之间的距离.
解 两条平行直线间的距离与一条平行线上的任意一点到另一条平行线的距离相等.因此在l1上取一点P(4,0)，则两条平行直线间的距离等于点P到直线l2的距离.d=3×4−4×0+632+42=185，即平行直线l1与l2之间的距离为185.
讲解
【发布任务】
例2由学生独立完成，教师根据学情点评，多鼓励表扬
引导学生将两平行直线间的距离转化为点到直线的距离
强调选点的技巧
巩固
【完成任务】
学生上台讲解
学生意识到直线上取点的任意性
1.学以致用，通过例题进一步领会点到直线的距离公式
2．树立学生的学习自信
3.从两点间的距离过渡到点到直线的距离再过渡到两平行直线的距离，层层递进，加深难度
（五）
课堂练习
【对照练习】
P37【随堂练习】填空题
【课堂检测】
见附录2
【发布任务】
让学生独立完成随堂练习后点评
【完成任务】
独立完成
加深点到直线距离公式的应用，提升学生数学运算的核心素养
（六）
课堂小结
点到直线的距离公式
【发布任务】
让学生自主归纳总结，多鼓励表扬参与者
【归纳总结】
学生积极参与课堂小结归纳，其它同学可作补充
提升学生归纳概括能力，巩固知识点
布置作业
数学学习指导与能力训练P28-29必做水平一、选做水平二
分层练习，满足不同层次学生需求
板书设计
6.7点到直线的距离公式
一、点到直线的距离公式 二、示范讲解 三、课堂练习
例


简明扼要，突出重点
课后拓展延伸
两条平行直线间的距离公式
反 思 诊 改
教学反思