中职数学北师大版（2021）拓展模块一 上册2.4.1 正弦定理公开课课件ppt

这是一份中职数学北师大版（2021）拓展模块一 上册2.4.1 正弦定理公开课课件ppt，文件包含北师大版《中职数学拓展模块一上册》第15课正弦定理课件pptx、北师大版《中职数学拓展模块一上册》第15课正弦定理教学设计docx等2份课件配套教学资源，其中PPT共17页， 欢迎下载使用。

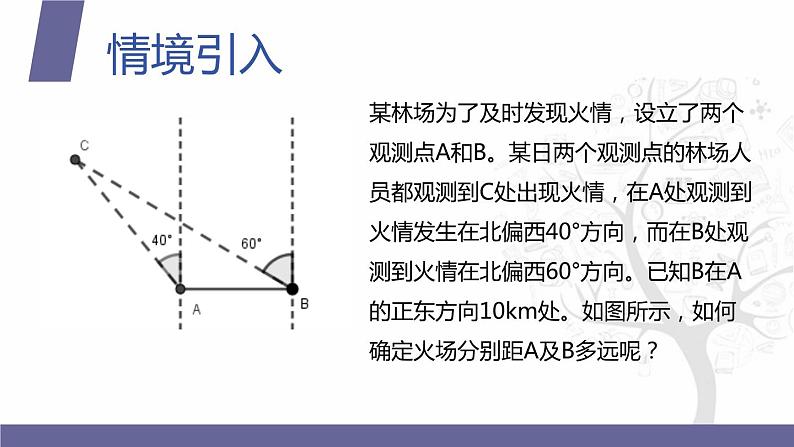
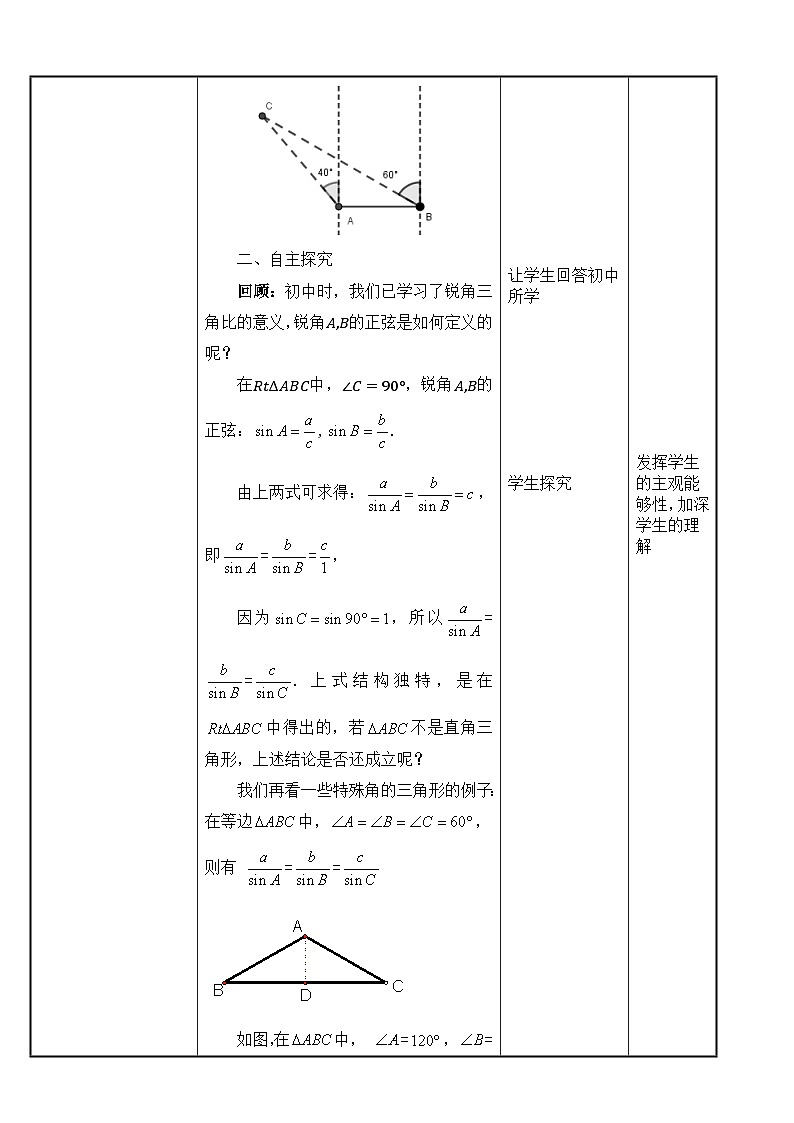
某林场为了及时发现火情，设立了两个观测点A和B。某日两个观测点的林场人员都观测到C处出现火情，在A处观测到火情发生在北偏西40°方向，而在B处观测到火情在北偏西60°方向。已知B在A的正东方向10km处。如图所示，如何确定火场分别距A及B多远呢？
问题1.初中时，我们已学习了锐角三角比的意义，锐角A,B的正弦是如何定义的呢？
在Rt△ABC中，∠C=90°，锐角A，B的正弦：
上式结构独特，是在Rt△ABC中得出的，若Rt△ABC不是直角三角形，上述结论是否还成立呢？
我们再看一些特殊角的三角形的例子：
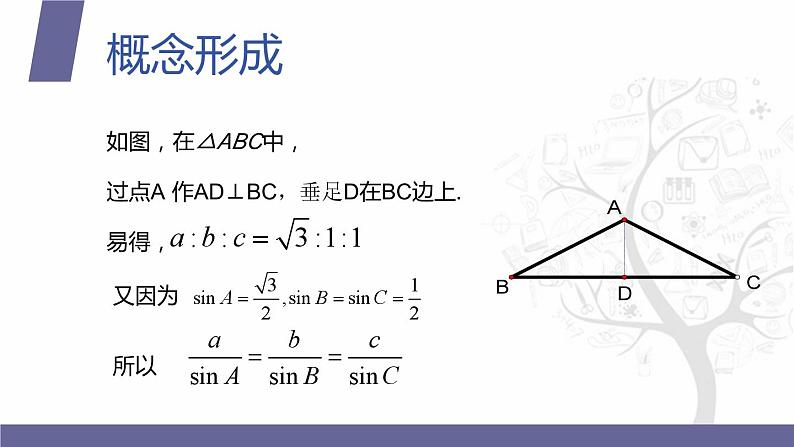
过点A 作AD⊥BC，垂足D在BC边上.
请同学们思考，对任意三角形，这个定理是否都成立呢？
对任意△ABC ，我们分别a,b,c用表示边BC,AC,AB，用A,B,C表示∠BAC, ∠ ABC, ∠ ACB。
当△ABC为锐角三角形时，如图所示，设CD为AB边上的高。根据三角函数的定义，得
当△ABC为钝角三角形时，同理上式依然成立。
因此，我们得出正弦定理
利用正弦定理解三角形，主要适用于以下两种情形：
（1）已知两角和一边，求其余两边与第三个角；
（2）已知两边和其中一边的对角，求其余两角与第三边。
教师借助GGB软件演示。
在三角形中，根据任意三角形的已知边、角，计算未知边、角的过程，叫做解三角形。
例3.将情境问题转化为数学问题：
本节课主要学习正弦定理，要注意正弦定理的应用条件。