数学拓展模块一 上册4.2.2 平面向量的减法公开课课件ppt

这是一份数学拓展模块一 上册4.2.2 平面向量的减法公开课课件ppt，文件包含北师大版《中职数学拓展模块一上册》第33课平面向量的减法课件pptx、北师大版《中职数学拓展模块一上册》第33课平面向量的减法教学设计docx等2份课件配套教学资源，其中PPT共16页， 欢迎下载使用。
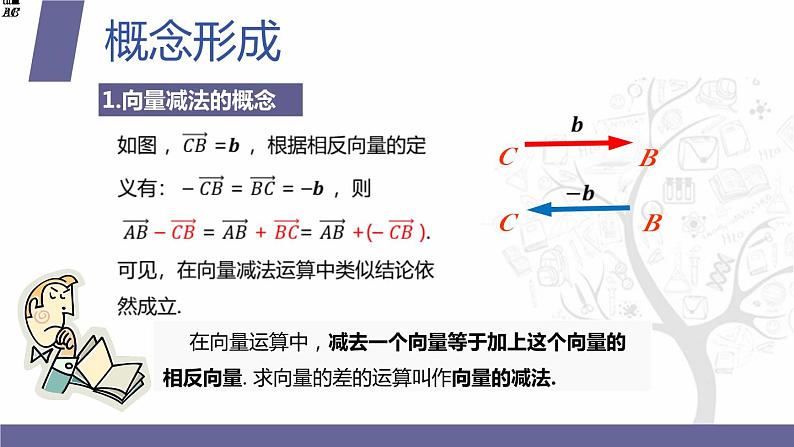
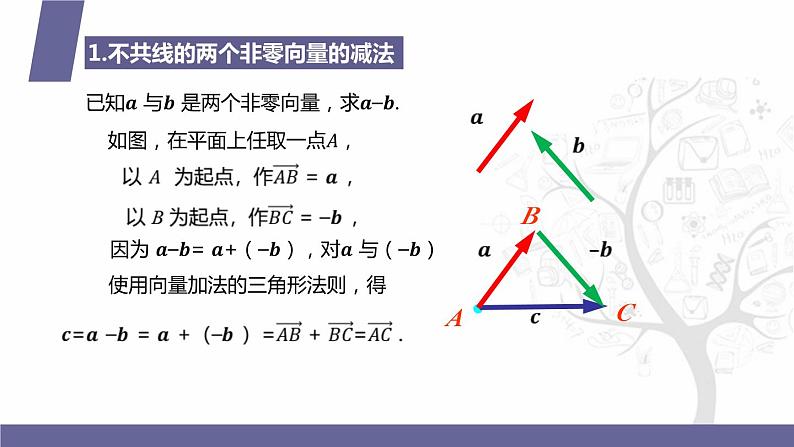
1.不共线的两个非零向量的减法
已知? 与? 是两个非零向量，求?–?.
如图，在平面上任取一点?，
因为 ?–?= ?+（–?），对? 与（–?） 使用向量加法的三角形法则，得
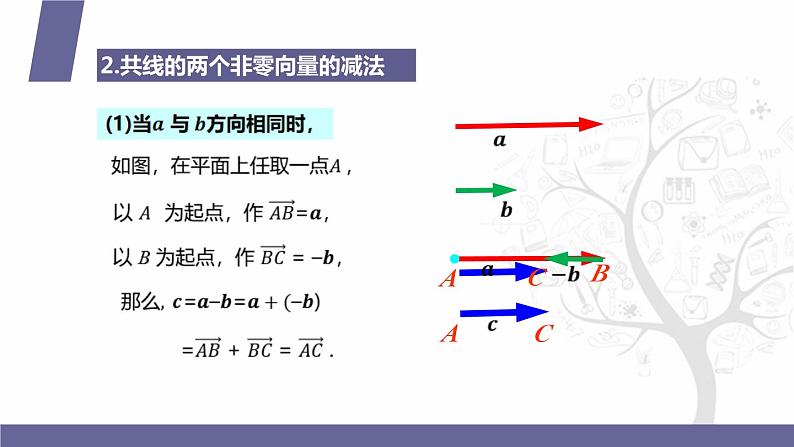
2.共线的两个非零向量的减法
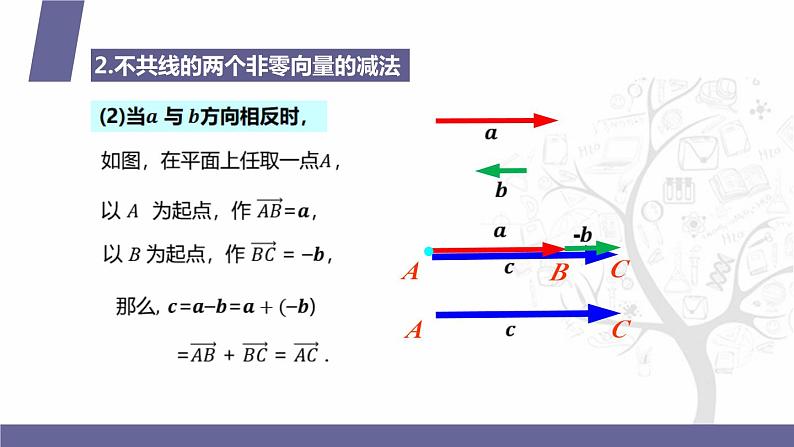
2.不共线的两个非零向量的减法
【解】以平面上任意一点? 为起点，
当向量?与?不共线时，把和向量?+?与差向量 ?–? 作在一个图上，可以得出什么结论?
向量减法作图的两种常用方法：
1.定义法向量?与?的差，就是向量?加上向量?的相反向量，即?–?= ?+（–?），此时?与（–?）仍遵循“首尾相接，由始至终”.
2.几何意义法把向量? 与向量? 平移到同一起点后，由向量? 的终点指向? 的终点的向量就是 ?–? .即“同一起点，减指被减”.(减向量指向被减向量)
2. 已知下列各组向量?，?，求作?+? 与 ?–?.
向量减法的定义： __________________________________ .
求向量差的运算叫做向量的减法
向量减法的运算法则：__ _________.
向量减法作图的两种常用方法：_______________________.