北师大版（2021）拓展模块一 上册5.2.1 双曲线的概念和标准方程优秀ppt课件

这是一份北师大版（2021）拓展模块一 上册5.2.1 双曲线的概念和标准方程优秀ppt课件，文件包含北师大版《中职数学拓展模块一上册》第43课双曲线的概念和标准方程课件pptx、北师大版《中职数学拓展模块一上册》第43课双曲线的概念和标准方程教学设计docx等2份课件配套教学资源，其中PPT共13页， 欢迎下载使用。

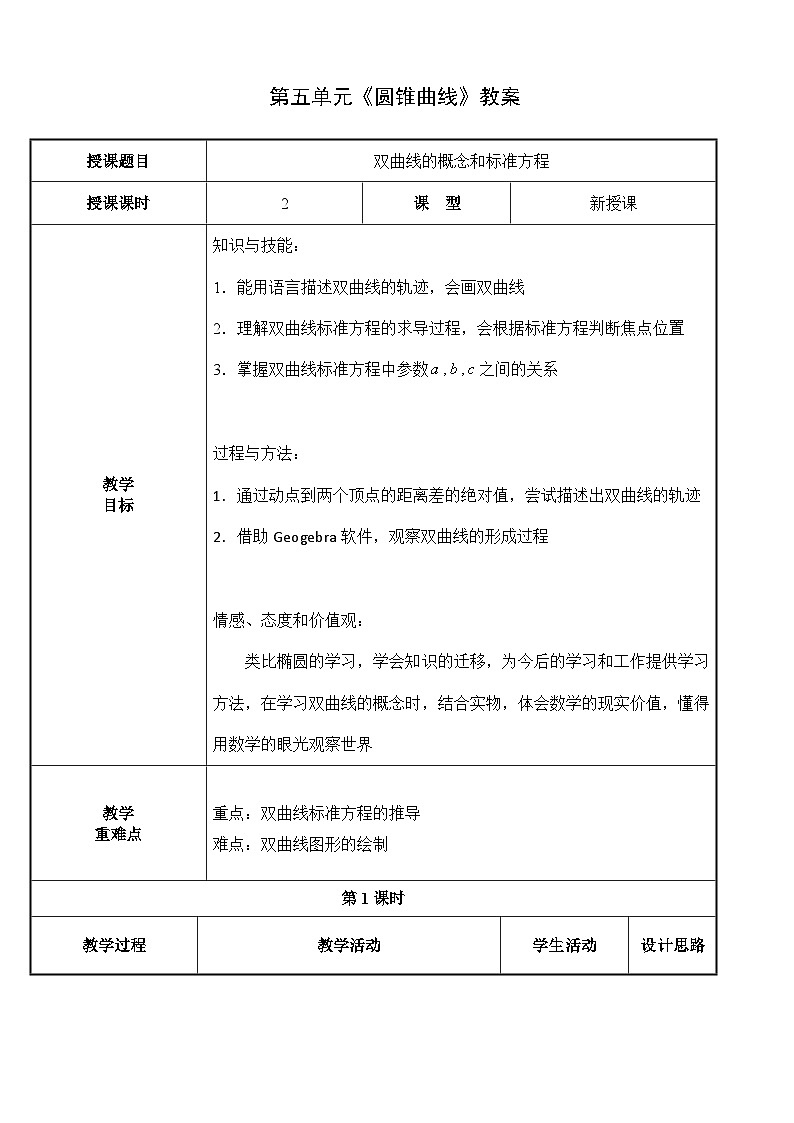
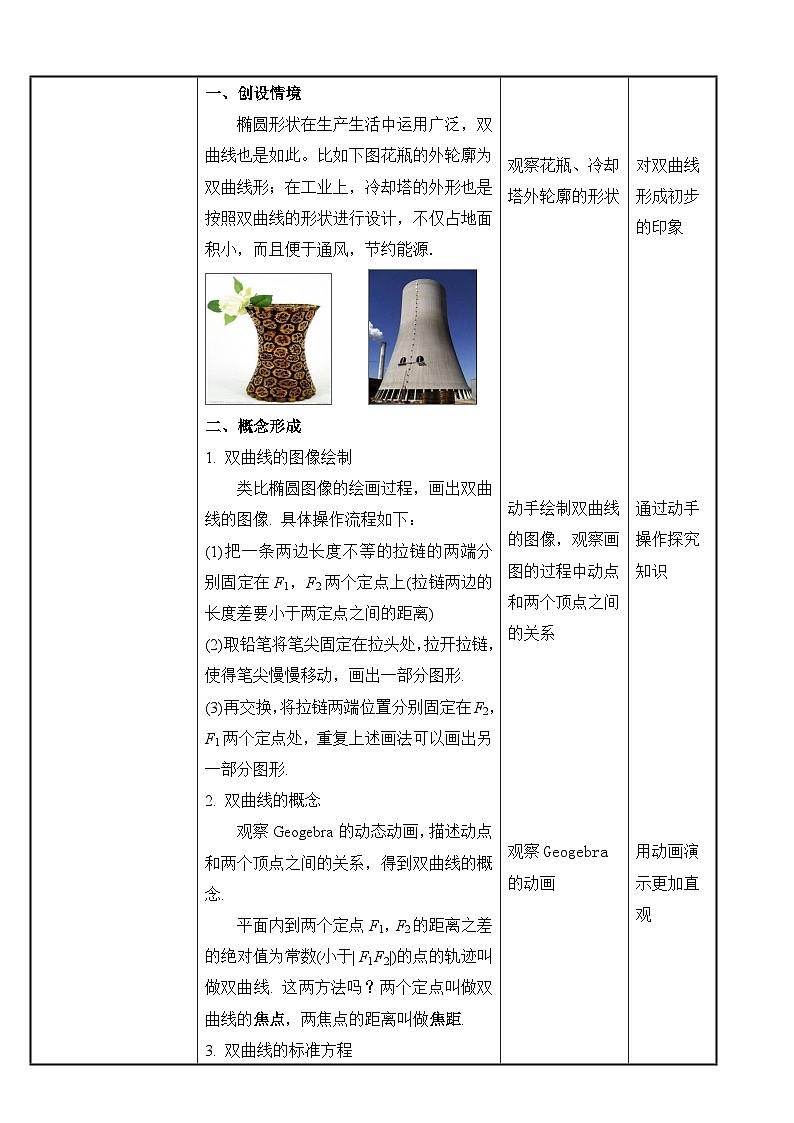
椭圆形状在生产生活中运用广泛，双曲线也是如此。比如下图花瓶的外轮廓为双曲线形；在工业上，冷却塔的外形也是按照双曲线的形状进行设计，不仅占地面积小，而且便于通风，节约能源.
5.1.1 双曲线的概念和标准方程
还记得画椭圆的方法吗？
参照画椭圆的方法，动手试一试，画一下双曲线.
(1)把一条两边长度不等的拉链的两端分别固定在F1，F2两个定点上(拉链两边的长度差要小于两定点之间的距离)
(2)取铅笔将笔尖固定在拉头处，拉开拉链，使得笔尖慢慢移动，画出一部分图形.
(3)再交换，将拉链两端位置分别固定在F2，F1两个定点处，重复上述画法可以画出另一部分图形.
当动点P在移动时，与两个定点F1，F2的距离之差的绝对值始终保持不变.
平面内到两个定点F1，F2的距离之差的绝对值为常数(小于| F1F2|)的点的轨迹叫做双曲线. 这两方法吗？两个定点叫做双曲线的焦点，两焦点的距离叫做焦距.
图中， F1，F2叫作焦点；
| F1F2|叫作焦距.
根据双曲线的定义可知：
|| MF1| ― | MF2||为定长
令|| MF1| ― | MF2||=2a，
| F1F2| =2c
|| MF1| ― | MF2||=2a
设M (x,y)， F1 (-c,0)， F2 (c,0)
即：| MF1| ― | MF2|=±2a
根据两点间距离公式，可得：
这个方程表示的是：焦点在 x 轴上的双曲线.
若双曲线的焦点在 y 轴上，其标准方程为：
焦点坐标为： F1 (0,-c)， F2 (0,c).
例1：已知双曲线的标准方程为 ，求焦点坐标和焦距.
例2：已知双曲线上任意一点到两焦点(0,-3)，(0,3)的距离差是2，求双曲线的标准方程.
1. 到两定点F1 (-4,0)， F2 (4,0)的距离之差的绝对值等于6的点的轨迹为（ ）
A. 椭圆B. 两条射线C. 双曲线D. 线段
2. 设双曲线 (m>0)的焦距为12，则m=（ ）
A. 1B. 2 C. 3 D. 4
3. 已知双曲线的标准方程为 ，求焦点坐标和焦距.