中职数学北师大版（2021）拓展模块一 上册6.1.2 平面的基本性质精品课件ppt

这是一份中职数学北师大版（2021）拓展模块一 上册6.1.2 平面的基本性质精品课件ppt，文件包含北师大版《中职数学拓展模块一上册》第49课平面的基本性质课件pptx、北师大版《中职数学拓展模块一上册》第49课平面的基本性质教学设计docx等2份课件配套教学资源，其中PPT共24页， 欢迎下载使用。

在铅球比赛中，裁判员用皮卷尺测量比赛成绩（如图6-9），如在测量时将皮卷尺拉得不够紧，测量的误差就比较大.那么，如何测量才能较为准确地反映实际成绩呢？
只要将皮卷尺的两端都紧贴着地面拉直，这样就可以保证它整体都紧贴着地面，这样可以较为准确地测量实际成绩.
从上述经验和类似的事实中可以归纳出以下公理.
公理1.如果一条直线上两点在一个平面内，那么这条直线在此平面内
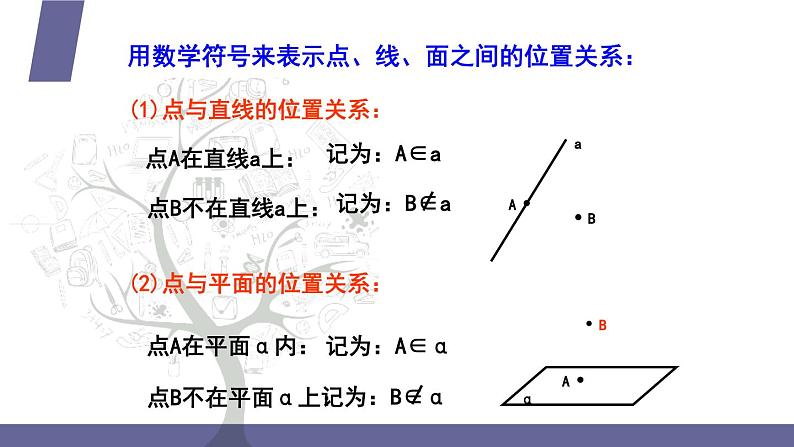
用数学符号来表示点、线、面之间的位置关系：
(1)点与直线的位置关系：
(2)点与平面的位置关系：
(3)直线与平面的位置关系：
直线a与平面α只有一个公共点A时，称直线a与平面α相交。　记为：a∩α＝A
直线a与平面α没有公共点时，称直线a与平面α平行。　记为：a//α
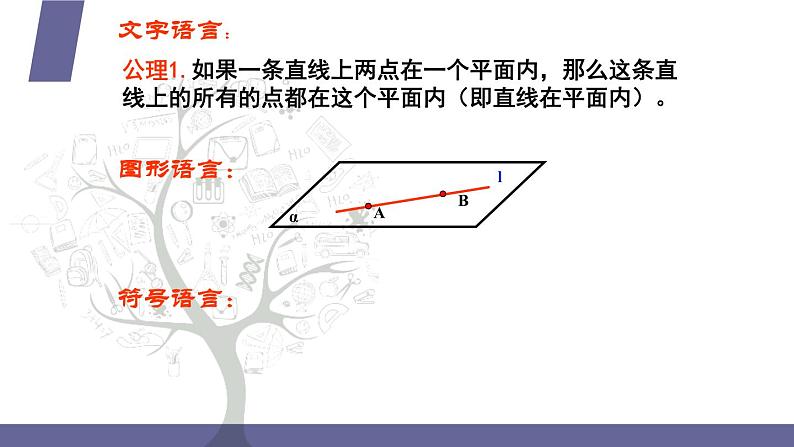
公理1.如果一条直线上两点在一个平面内，那么这条直线上的所有的点都在这个平面内（即直线在平面内）。
一 是可以用来判定一条直线是否在平面内，即 要判定直线在平面内，只需确定直线上两个 点在平面内即可；
二 是可以用来判定点在平面内，即如果直线在 平面内、点在直线上，则点在平面内.
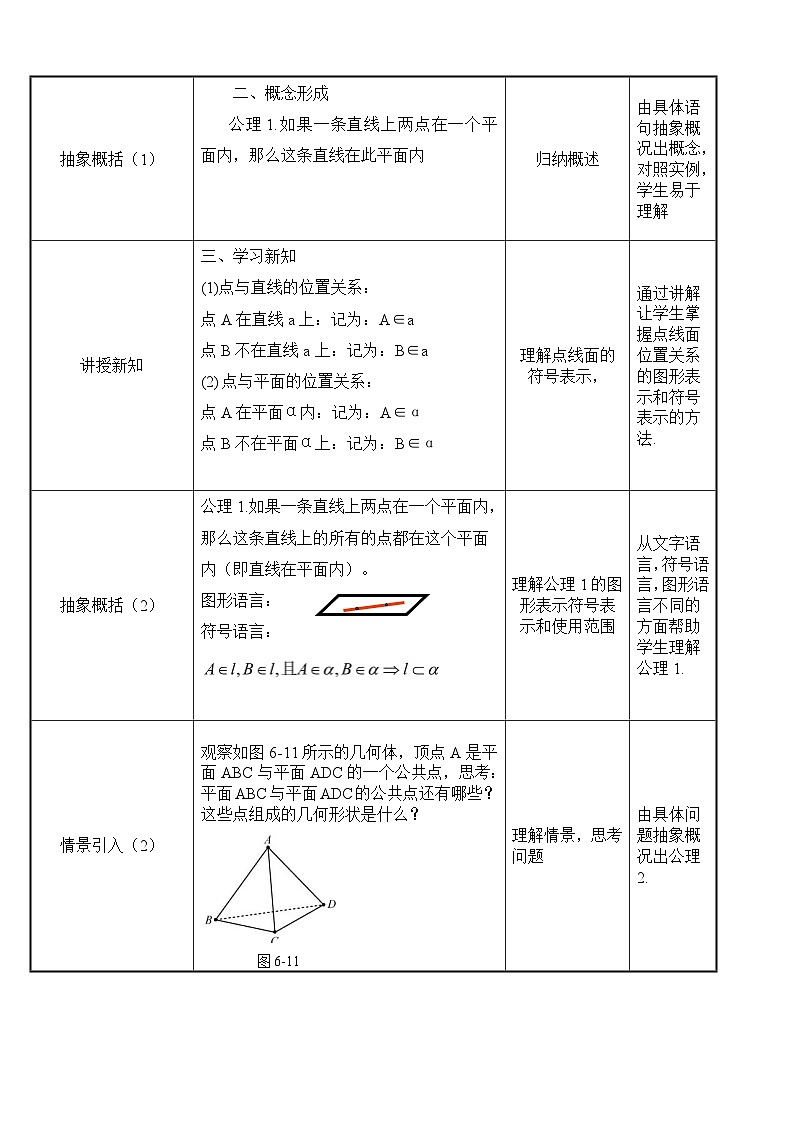
观察如图6-11所示的几何体，顶点A是平面ABC与平面ADC的一个公共点，思考：平面ABC与平面ADC的公共点还有哪些？这些点组成的几何形状是什么？
答：点C也是平面ABC与平面ADC的一个公共点，线段AC上的任意一点都是平面ABC与平面ADC的一个公共点.
从上述观察和类似的事实中可以归纳出以下公理.
公理2.如果不重合的两个平面有一个公共点，那么它们有且只有一条过该点的公共直线.
一 是判定两个平面相交，即如果两个平面有一个 公共点，那么这两个平面相交；
二 是判定点在直线上，即点若是某两个平面的公 共点，那么这点就在这两个平面的交线上.
三.两平面两个公共点的连线就是它们的交线
观察如图6-13的自行车的结构，自行车的后轮胎附近设置了一个脚撑，这个脚撑的作用是什么？
答：自行车有两个支点时，不足以将自行车停稳.当脚撑放下来的时三个支点就可以将自行车停稳
经过不在同一直线上的三点，有且只有一个平面.
公理3.经过不在同一直线上的三点，有且只有一个平面.
公理3的作用:确定平面的依据;
【例1】在长方体ABCD—A1B1C1D1中，画出平面A1C1D与平面B1D1D的交线.
推论1.经过一条直线和直线外一点，有且只有一个平面。
推论2.经过两条相交直线有且只有一个平面。
推论3.经过两条平行直线有且只有一个平面。
【例2】用集合的语言表示下列语句（1）点A在平面α内，但是在平面β；（2）直线l和直线m在平面α内，且相交于点A；（3）平面α与平面β的交线l与直线m交于点A．
2、根据下列符号表示的语句，说出有关点、 线、面的关系，并画出图形. （1）（2）（3）（4）
①理解平面基本性质中三个公理以及公理三的三个推论。②掌握平面基本性质的三种表示方法: 文字表示， 几何表示和符号表示。
3.情感、态度与价值观
借助于铅球距离测量，自行车支架等生活中的例子引导学生理解平面基本性质。
①通过对平面的基本性质的理解提高学生的抽象概括能力。②通过本节学习和运用实践，培养学生的逻辑思维能力和准确运用数学符号的意识。