中职数学北师大版（2021）拓展模块一 上册6.2.1 平行直线优秀课件ppt

这是一份中职数学北师大版（2021）拓展模块一 上册6.2.1 平行直线优秀课件ppt，文件包含北师大版《中职数学拓展模块一上册》第50课平行直线课件pptx、北师大版《中职数学拓展模块一上册》第50课平行直线教学设计docx等2份课件配套教学资源，其中PPT共14页， 欢迎下载使用。
在室内存在很多具有平行关系的线，能否指出下图中具有平行关系的线？ 并在你所在的教室中，指出具有平行关系的线。
只要将皮卷尺的两端都紧贴着地面拉直，这样就可以保证它整体都紧贴着地面，这样可以较为准确地测量实际成绩.
从上述经验和类似的事实中可以归纳出以下公理.
定义.我们把同一平面内不相交的两条直线叫作平行线.
平行公理：过直线外一点有且只有一条直线与这条直线平行.
平行性质 平行于同一直线的两条直线互相平行.
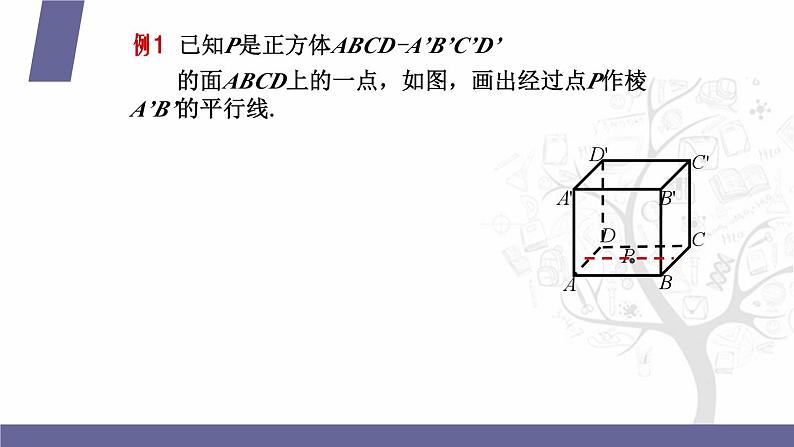
例1 已知P是正方体ABCD-A’B’C’D’ 的面ABCD上的一点，如图，画出经过点P作棱 A’B’的平行线.
将平面α内的四边形ABCD的两条边AD与DC沿着对角线AC向上折起，将点D折叠到点D1的位置（如图6-19）．折叠过程中，哪些量发生了变化，哪些量没有发生变化，相互之间的关系有哪些变化.
在折叠过程中，线段AD，DC，CB，BA，AC的长度不变，但是BD的长度在变化.没折叠之前，A，B，C，D四个点都在同一个平面内，将点D折叠到点D1的位置后，四个点就不在同一个平面内了．
每个点叫作空间四边形的顶点，相邻点间的线段叫作空间四边形的边，两个不相邻点的线段叫作空间四边形的对角线.空间四边形一般用顶点的四个字母表示．例如，图6-20中的四边形叫作空间四边形ABCD，其中AC，BD是它的对角线.
顺次连接不共面的四点所构成的图形，叫作空间四边形.
例1 如图6-21所示，已知空间四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点.求证：四边形EFGH是平行四边形.
思考：取一块长方形纸板ABCD，E、F分别为AB、 CD的中点，将纸板沿EF折起，在空间中直线AD与BC的位置关系如何?
观察：在长方体ABCD-A’B’C’D’中，BB’∥AA’， DD’∥ AA’，则BB’与DD’是否平行呢?
判断：四棱柱ABCD-A’B’C’D’的底面ABCD是平行四边形，则∠BAD与∠B’A’D’，∠BAD与∠ADC的大小关系如何?
等角定理：如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补.。
要求适合某种条件且与已知角终边相同的角，其方法是先求出与已知角终边相同的角的一般形式，再依条件构建不等式求出k的值。
1.关于空间四边形, 下列结论正确的是( ). A.四个顶点不共面 B.两条对角线交于一点 C.梯形是空间四边形 D.空间四边形中可以有两条边平行 2.三条直线两两平行可以确定的平面的个数为( ). A.1个 B.2个 C.1个或3个 D.2个或4个 3.平行于 的两条直线平行, 过直线外一点有且只有 条直线与已知直线平行.
①理解平行公理，等角定理。②理解空间四边形的概念。
3.情感、态度与价值观
借助于教室，卧室空间中的平行关系引导学生了解平行公理的概念，帮助学生建立空间中直线与直线的位置关系
①通过对平行公理和等角定理的理解提高学生的抽象能力。②通过本节学习和运用实践，培养学生空间想象能力和逻辑思维能力。