数学拓展模块一 上册6.2.2 异面直线一等奖ppt课件

这是一份数学拓展模块一 上册6.2.2 异面直线一等奖ppt课件，文件包含北师大版《中职数学拓展模块一上册》第51课异面直线课件pptx、北师大版《中职数学拓展模块一上册》第51课异面直线教学设计docx等2份课件配套教学资源，其中PPT共14页， 欢迎下载使用。

观察立交桥所在直线的位置关系如何？
问题1：在同一平面内，两条直线有几种位置关系？空间中两条直线还有没有其他位置关系？
①直线AB与DC在同一个平面ABCD内，它们没有公共点，它们是平行直线.
②直线AB与BC在同一个平面ABCD内，它们只有一个公共点B，它们是相交直线.
③直线AB与CC'不同在任何一个平面内.
不同在任何一个平面内的两条直线叫做异面直线.
问题2：在长方体中,直线AB与DC在同一个平面内吗？它们有没有公共点？它们的位置关系如何？直线AB与BC呢？直线 AB 与 CC’呢？
空间直线与直线的位置关系
在同一平面内，有且只有一个公共点；
在同一平面内，没有公共点；
不同在任何一个平面内，没有公共点.
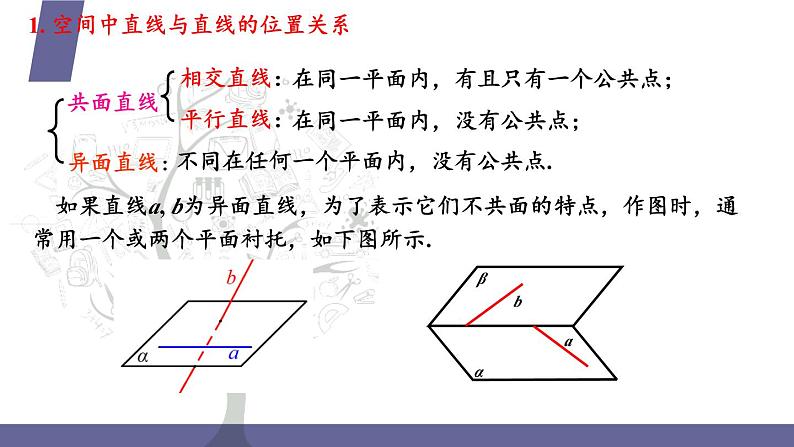
1. 空间中直线与直线的位置关系
如果直线a, b为异面直线，为了表示它们不共面的特点，作图时，通常用一个或两个平面衬托，如下图所示.
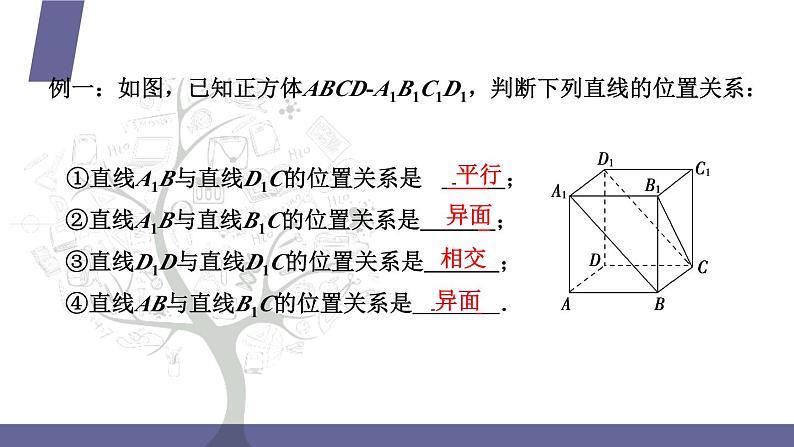
例一：如图，已知正方体ABCD­A1B1C1D1，判断下列直线的位置关系：
①直线A1B与直线D1C的位置关系是 ；②直线A1B与直线B1C的位置关系是 ；③直线D1D与直线D1C的位置关系是 ；④直线AB与直线B1C的位置关系是 ．
异面直线a和b，在空间任取一点P， 过P分别作a和b的平行线a’和b’
则直线a’和b’所成的锐角(直角)叫做异面直线a和b所成的角.
由等角定理，直线a和b所成角的大小与点P位置无关，即可适当选取.
则异面直线所成的角的范围：(0º , 90º ].
例1 如图6-26所示, 在正方体ABCD-A'B'C'D'中, 图6-26 (1)哪些棱所在的直线与直线BA'是异面直线? (2)直线BA'与CC'的夹角是多少? (3)哪些棱所在的直线与直线AA'垂直?
解 : (1)由异面直线的定义可知, CD, DA, CC', DD', B'C', C'D' 所在的直线分别与直线BA'异面. (2)因为BB'∥CC', 所以∠A'BB'为BA'与CC'的夹角. 由正方体的性质知∠A'BB'=45°, 所以直线BA'与CC'的夹角是45°. (3)直线AB, BC, CD, DA, A'B', B'C', C'D', D'A'所在的直线 分别与直线AA'垂直.
例2、在正方体ABCD—A1B1C1D1中，求：（1）A1B与CC1所成的角；（2） A1B1与C1C所成的角； （3）A1C1与D1C所成的角。
例3 如图6-27所示, 在正方体ABCD-A1B1C1D1 中, E, F, G, H 分别为AA1, AB, BB1, B1C1 的中点, 求异面直线EF与GH所成的角的大小.
解 :如图6-28，连接A1B，BC1，A1C1．因为 E，F，G，H分别为AA1，AB，BB1，B1C1的中点，所以 EF，GH分别是ΔABA1，ΔB1BC1的中位线，所以 EF／／A1B，GH／／BC1，所以 ∠A1BC1为EF与GH所成的角．因为A1B，BC1，C1A1是正方体三个面的对角线， 所以ΔBA1C1是等边三角形，所以∠A1BC1＝60°，所以直线EF与GH所成的角的大小为60°
要求适合某种条件且与已知角终边相同的角，其方法是先求出与已知角终边相同的角的一般形式，再依条件构建不等式求出k的值。
1．下列结论正确的是（ ).A.分别在两个平面内的直线是异面直线B.没有公共点的直线是平行直线C.两条垂直直线必定相交D.不同在任何一个平面内的两条直线是异面直线2．两条异面直线所成的角的范围是（ ).A.(0°,90) B.(0°,90°] C.[0°,90) D.[0°,90°]3．空间两条直线的位置关系有 、 和
4 已知正方体ABCD-A’B’C’D’的棱长为a， 求下列异面直线所成的角的大小：
（1）AB 与 B’C’；
解：由BC//B’C’，
即AB与B’C’所成角为∠ ABC，
又∠ABC = 90º，
则AB与B’C’所成角为90º.
（2）A’B与CC’；
则A’B与CC’所成角为45º.
（3）AB’与BC’.
则AB’与BC’所成角为60º.
定位：作(找)平行线，求证所求角；定量：解三角形，计算角的大小.
①理解平行公理，等角定理。②理解空间四边形的概念。
3.情感、态度与价值观
借助于中间中的平行关系引导学生了解平行公理的概念，帮助学生建立空间中直线与直线的位置关系
①通过对平行公理和等角定理的理解提高学生的抽象能力。②通过本节学习和运用实践，培养学生空间想象能力和逻辑思维能力。