数学拓展模块一 上册第六单元 立体几何6.3 直线与平面的位置关系6.3.2 直线与平面垂直精品ppt课件

这是一份数学拓展模块一 上册第六单元 立体几何6.3 直线与平面的位置关系6.3.2 直线与平面垂直精品ppt课件，文件包含北师大版《中职数学拓展模块一上册》第53课直线与平面垂直课件pptx、北师大版《中职数学拓展模块一上册》第53课直线与平面垂直教学设计docx等2份课件配套教学资源，其中PPT共15页， 欢迎下载使用。
随着人们对于建筑空间利用的追求，折叠门（如图6-35）也逐渐受到青睐。折叠门向两边推的过程中，观察门轴线AB、门下框线AC和AD三者之间的位置关系如何.
折叠门在向两边推的过程中，直线AC和AD是地面上两条相交直线，直线AB和AC，AD始终保持垂直，我们观察发现门轴线AB和地面的关系也一直是垂直关系.
上述事例中提到了“线面垂直”，我们先给出空间直线与平面垂直的定义.
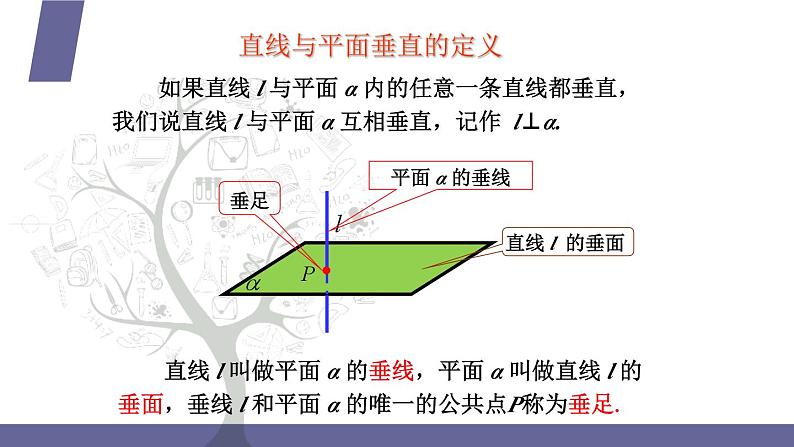
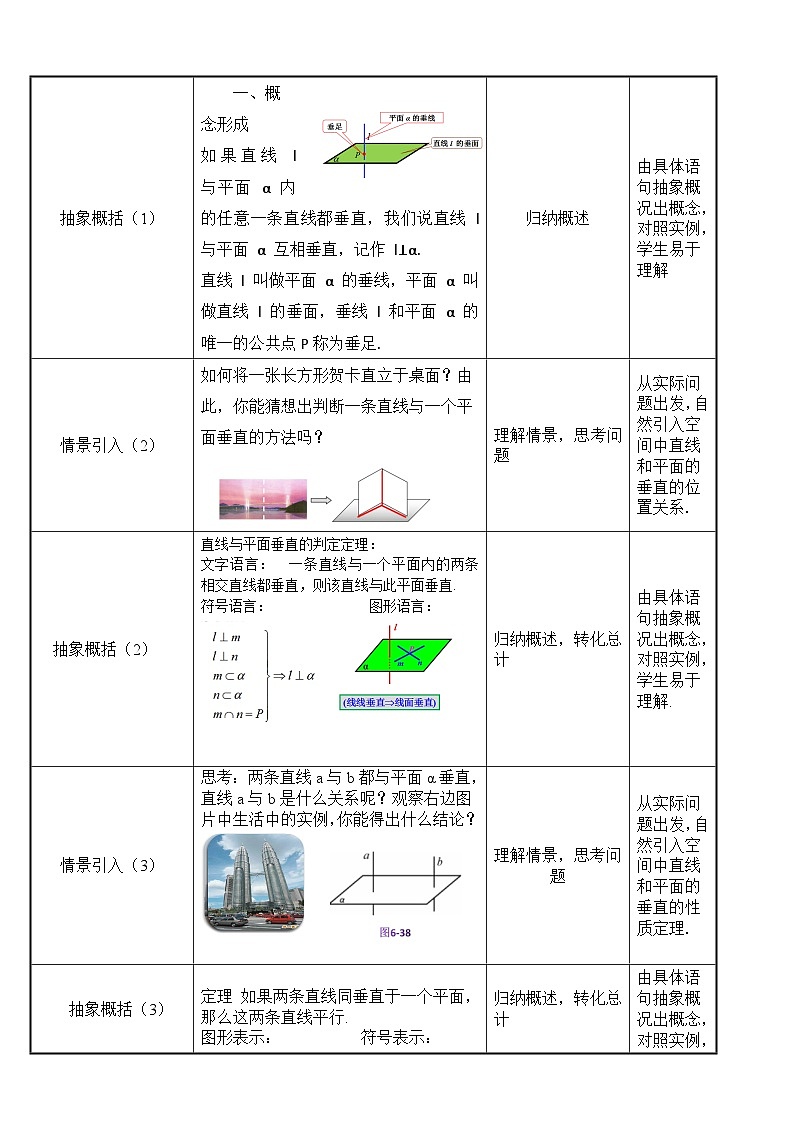
如果直线 l 与平面 α 内的任意一条直线都垂直，我们说直线 l 与平面 α 互相垂直，记作 l⊥α.
直线 l 叫做平面 α 的垂线，平面 α 叫做直线 l 的垂面，垂线 l 和平面 α 的唯一的公共点P称为垂足.
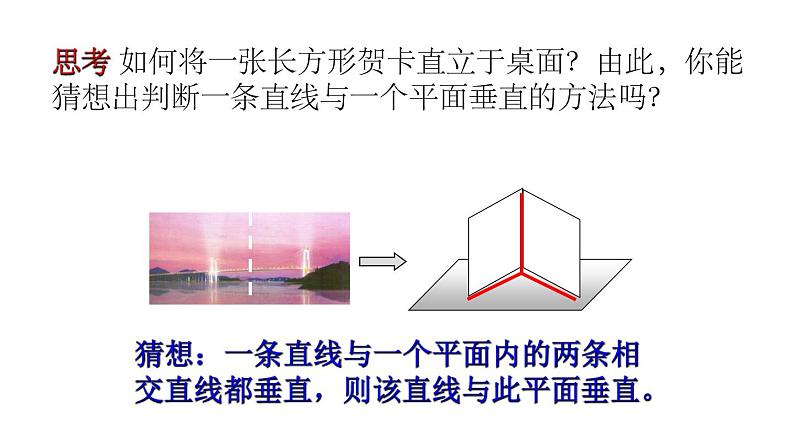
思考 如何将一张长方形贺卡直立于桌面？由此，你能猜想出判断一条直线与一个平面垂直的方法吗？
猜想：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。
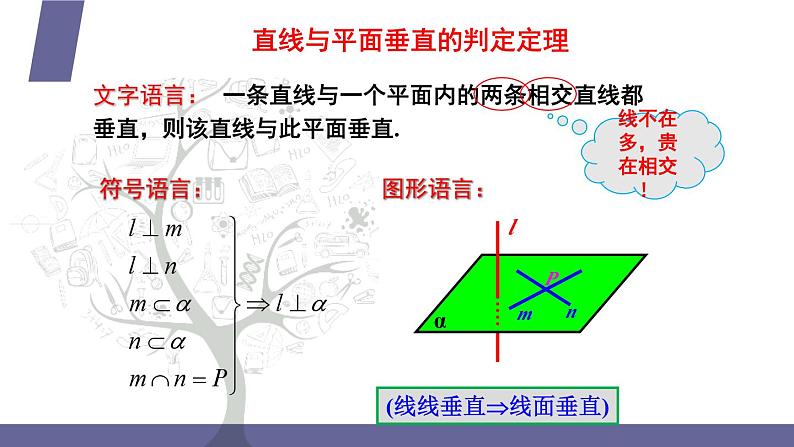
文字语言： 一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直.
(线线垂直线面垂直)
直线与平面垂直的判定定理
例1 求证：如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于这个平面．
推论 如果在一组平行直线中，有一条直线垂直于平面，那么另外的直线也垂直于平面.
思考：两条直线a与b都与平面α垂直，直线a与b是什么关系呢？观察右边图片中生活中的实例，你能得出什么结论？
定理 如果两条直线同垂直于一个平面，那么这两条直线平行.
例1 如图6-39，在三棱锥P-ABC中，点E是BC的中点，PB＝PC，AC＝AB，求证：BC1平面PAE．
分析:设法在平面ＢＣＤ内找一条直线与ＥＦ平行
证明：连接PE，AE.因为 PB＝PC，AB＝AC，E是BC的中点，所以 PE⊥BC，AE⊥BC.又因为PE与AE是平面PAE内的两条相交直线，所以BC⊥平面PAE.
例2 .如图6-40，已知平面a∩平面β＝CD，PA⊥ α，垂足是A，PB⊥ β，垂足是B.求证：CD⊥AB.
分析: 可以先证明直线CD⊥平面PAB，接下来由直线与平面垂直的性质得到CD⊥AB.
证明：因为PA⊥a，CD a， 所以 PA⊥CD.同理 PB⊥CD.又因为 PA与PB交于点P，所以 CD⊥平面PAB.又因为 AB 平面PAB，所以 CD⊥AB.
1.判断下列命题是否正确,正确的打“√”错的打“×”.
（4）若一条直线与一个平面不垂直,则这个平面内没有与这条直线垂直的直线.
（1）若一条直线与一个三角形的两条边垂直,则这条直线垂直于三角形所在的平面.
（2）若一条直线与一个平行四边形的两条边垂直，则这条直线垂直于平行四边形所在的平面.
（3）若一条直线与一个梯形的两腰垂直，则这条直线垂直于梯形所在的平面.
2. 如图, M是菱形ABCD在平面外一点，满足MA=MC. 求证: AC⊥平面BDM.
证明：∵在菱形ABCD中，点O是AC的中点， 且MA=MC，∴AC⊥OM ∵在菱形ABCD中，AC⊥BD 又OM∩BD=O，OM 平面BDM， BD 平面BDM ∴AC⊥平面BDM
①理解直线和平面的位置关系，线面垂直的判定定理。②掌握线面垂直判定定理的文字表示，符号表示，图形表示。
3.情感、态度与价值观
借助生活中推拉门引入入直线和平面的垂直的概念以及线面垂直的判定定理，引导学生建立数学图形和数学符号之间的联系。
①通过对空间中线面垂直概念和判定的理解提高学生的抽象能力。②通过本节学习，培养学生空间想象能力和逻辑推理能力。