山东省菏泽市牡丹区2023-2024学年八年级下学期3月月考数学试卷(含答案)

这是一份山东省菏泽市牡丹区2023-2024学年八年级下学期3月月考数学试卷(含答案)，共21页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．在单位长度为1的正方形网格中，下面的三角形是直角三角形的是( )
A.B.C.D.
2．已知，则下列各式中一定成立的是( )
A.B.C.D.
3．兔子的三个洞口构成，猎狗想捕捉兔子，必须到三个洞口的距离都相等，则猎狗应蹲守在( )
A.三条中线的交点处B.三条高的交点处
C.三条边的垂直平分线的交点处D.三条角平分线的交点处
4．已知关于x的不等式（a﹣1）x＞2的解集为，则a的取值范围是( )
A.a＜1B.a＞1C.a＜0D.a＞0
5．如图，中，，且，垂直平分，交于点F，交于点E，若周长为，，则的长为( )
A.5B.8C.9D.10
6．规定表示m，n中较小的数（m，n均为实数，且），若，则x的取值范围是( )
A.B.C.D.
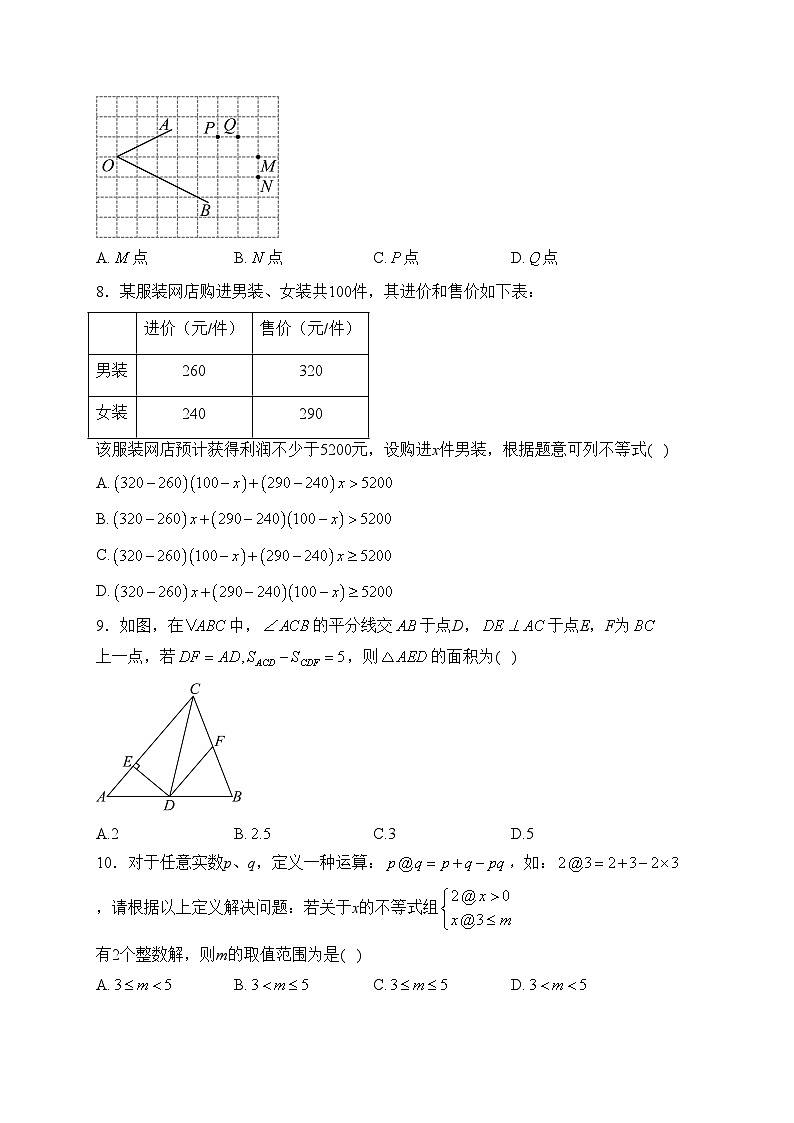
7．在正方形网格中，的位置如图所示，到两边距离相等的点应是( )
A.点B.点C.点D.点
8．某服装网店购进男装、女装共100件，其进价和售价如下表：
该服装网店预计获得利润不少于5200元，设购进x件男装，根据题意可列不等式( )
A.
B.
C.
D.
9．如图，在中，的平分线交于点D，于点E，F为上一点，若，则的面积为( )
A.2B.C.3D.5
10．对于任意实数p、q，定义一种运算：，如：，请根据以上定义解决问题：若关于x的不等式组 有2个整数解，则m的取值范围为是( )
A.B.C.D.
二、填空题
11．中，，高，则的长为______.
12．若不等式组无解，则m的取值范围为______.
13．如图，在中， ，分别以A、C为圆心，大于AC的一半的长度为半径画弧，四弧交于两点M、N,作直线MN，交于点，交于点.已知∠C=32°，则∠BAE的度数为______度.
14．已知不等式的解集是，则a的取值范围是______.
15．一个三位数A.它的各个数位上的数字均不为零，且满足百位上数字与个位上数字的和等于十位上数字的两倍，则称这个三位数为“最优数”，将“最优数”A的百位数字与个位数字交换位置后得到的新数记为，另记A和的和为.例如：246满足，则246是“最优数”，且.已知“最优数”的百位数字小于个位数字，且能被8整除，则满足条件的“最优数”的最大值为______.
16．如图，在中，以，为直角边分别作等腰直角三角形，连接，与交于点，连接，，，，.下列结论：
①；
②；
③平分；
④，其中正确结论的为______.
三、解答题
17．计算：
(1)解不等式：.
(2)求不等式的正整数解.
18．已知：如图中，，平分，平分，过D作直线平行于交，于E，F.
(1)求证：是等腰三角形；
(2)求的周长.
19．已知关于x，y的二元一次方程组的解满足，求满足条件的m的所有非负整数值.
20．如图，AB＝BC，∠BAD＝∠BCD＝90°，点D是EF上一点，AE⊥EF于E，CF⊥EF于F，AE＝CF，求证：Rt△ADE≌Rt△CDF.
21．某礼品店准备从厂家选购甲、乙两种毛绒玩具，若购进甲种毛绒玩具3个和乙种毛绒玩具2个共需310元；若购进甲种毛绒玩具5个和乙种毛绒玩具6个共需730元.
(1)求购进每个甲种、乙种毛绒玩具的价钱分别为多少元？
(2)若该礼品店每销售1个甲种毛绒玩具可获利15元，每销售一个乙种毛绒玩具可获利20元，且该礼品店将购进甲、乙两种毛绒玩具共50个全部售出后，要获得的利润不少于800元，问甲种毛绒玩具最多购进多少个？
22．如图，在中，，，G为的中点，交的平分线于D，于E，于F交的延长线于F.
(1)求证：；
(2)求的长.
23．某动物园在周年庆来临之际，推出、两种纪念章，已知每个种纪念章的进价比每个种纪念章的进价多4元；购进6件种纪念章和购进10件种纪念章的费用相同，且种纪念章售价为13元/个，种纪念章售价为8元/个.
(1)每个种纪念章和每个种纪念章的进价分别是多少元？
(2)根据网上预约的情况，该园计划用不超过2800元的资金购进、两种纪念章共400个，这400个纪念章可以全部销售，选择哪种进货方案，该园获利最大？最大利润是多少元？
24．【问题背景】如图1，在四边形中，，分别是上的点，且，试探究图中线段之间的数量关系.
【初步探索】小亮同学认为：如图1，延长到点，使，连接，先证明，再证明，可得出结论______；
【探索延伸】如图2，在四边形中，分别是上的点，，上述结论是否仍然成立？说明理由.
【结论运用】如图3，在某次军事演习中，舰艇甲在指挥中心（处）北偏西的处，舰艇乙在指挥中心南偏东的处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东的方向以80海里/小时的速度前进1.5小时后，指挥中心观测到甲、乙两舰艇分别到达处，且两舰艇之间的夹角为，试求此时两舰艇之间的距离.
【灵活变通】如图4，已知在四边形中，，若点在的延长线上，点在的延长线上，仍然满足【初步探索】中的结论，请直接写出与的数量关系.
参考答案
1．答案：C
解析：A、三角形的三边为，，3，，则这个三角形不直角三角形，本选项不符合题意；
B、三角形的三边为，，，，则这个三角形不直角三角形，本选项不符合题意；
C、三角形的三边为，，，，则这个三角形是直角三角形，本选项符合题意；
D、三角形的三边为，，，这个三角形不直角三角形，本选项不符合题意；
故选：C.
2．答案：D
解析：A.不等式两边同时减b，可得，选项一定不成立，不符合题意；
B.当时，可得，选项不一定成立，不符合题意；
C.不等式两边同时除以2再减去1，可得，选项一定不成立，不符合题意；
D.不等式两边同时乘，可得，选项一定成立，符合题意；
故选：D.
3．答案：C
解析：∵兔子的三个洞口构成，猎狗想捕捉兔子，必须到三个洞口的距离都相等，
设猎狗在点，则，
∴点在线段的垂直平分线上，
同理，点在线段，的垂直平分线上，
∴猎狗应蹲守在在三条边的垂直平分线的交点处，
故选：C.
4．答案：A
解析：∵关于x的不等式（a﹣1）x＞2的解集为，，
∴a﹣1＜0，
∴a＜1，
故选：A.
5．答案：A
解析：∵，且，
∴
∵垂直平分，
∴
∵周长
∴
即：
∴
故选：A
6．答案：D
解析：由题意得：，
解得：；
故选D.
7．答案：A
解析：如图，连接，
根据网格得出，，
在与中
∴，
∴，
即平分
∴到两边距离相等的格点应是点，
故选A.
8．答案：D
解析：设购进x件男装，则购进件女装，根据题意，得
故选：D.
9．答案：B
解析：如图，在上截取，连接，如图所示：
∵平分，
∴，
在和中，
，
∴，
∴，，
∵，
∴，即.
∵，
∴，
∴，
∴.
故选：B.
10．答案：A
解析：∵，
∴，
解不等式①得：，
解不等式②得：，
∴不等式组的解集是，
∵不等式组有2个整数解，
∴，
解得：，
故选：A.
11．答案：4或14
解析：如图，是锐角三角形时，
∵在中，，
∴，
∴，
在中，，由勾股定理得
，
∴，
∴的长为；
如图，是钝角三角形时，
∵在中，，
∴，
∴，
在中，，由勾股定理得
，
∴，
∴的长为.
故答案为14或4.
12．答案：
解析：∵不等式组无解，
∴
∴
故答案为.
13．答案：26
解析：∵∠B=90°，∠C=32°，
∴∠BAC=90°-32°=58°.
由题意可知：直线NM为线段AC的垂直平分线，
∴AE=CE，
∴∠EAC=∠C=32°，
∴∠BAE=∠BAC-∠EAC=58°-32°=26°.
故答案为：26.
14．答案：
解析：由不等式组的解集是，
因此a的取值范围是.
故答案为：.
15．答案：789
解析：设的百位数字为a，十位数字为b，个数数字为c，且，
∴，
∴，，
∴
，
∴，
∵能被8整除，且，
∴或，
∴或，
∵要使M最大，必须使取最大值，
∴当时，M才能取到最大值，
∴，
∵，，，
∴，时，M最大，且最大值为789.
故答案为：.
16．答案：①②③④
解析：∵，，，
，
，
，，故①正确，
设和交于点，过作于，于，
∵，
∴，即，
∵，
，
，即平分，故③正确，
，
，
，故②正确，
，，，，
，故④正确，
故答案为：①②③④.
17．答案：(1)
(2)正整数解为
解析：（1）去括号得：，
移项合并得：，
系数化为1得：；
（2）去分母得：，
去括号得：
移项合并得：，
所以正整数解为.
18．答案：(1)见解析
(2)
解析：（1）证明：，
，
平分，
，
，
，
∴是等腰三角形；
（2），
，
平分，
，
，
，
，，
∴的周长为：
.
19．答案：满足条件的m的所有非负整数值为：0，1，2.
解析：，
得：，
.
把代入②得，
，
.
，
，
，
所以满足条件的m的所有非负整数值为：0，1，2.
20．答案：见解析
解析：连接BD，
∵∠BAD＝∠BCD＝90°，
在Rt△ABD和Rt△CBD中，
，
∴Rt△ABD≌Rt△CBD（HL），
∴AD＝CD，
∵AE⊥EF于E，CF⊥EF于F，
∴∠E＝∠F＝90°，
在Rt△ADE和Rt△CDF中，
，
∴Rt△ADE≌Rt△CDF（HL）.
21．答案：(1)购进每个甲种毛绒玩具的价钱为50元，购进每个乙种毛绒玩具的价钱为80元
(2)甲种毛绒玩具最多购进40个
解析：（1）设购进每个甲种毛绒玩具的价钱为x元，购进每个乙种毛绒玩具的价钱为y元，
由题意得：，
解得：，
答：购进每个甲种毛绒玩具的价钱为50元，购进每个乙种毛绒玩具的价钱为80元；
（2）设购进甲种毛绒玩具m个，
由题意得：，
解得：，
答：甲种毛绒玩具最多购进40个.
22．答案：(1)见解析
(2)
解析：（1）如图，连接，，
∵G是的中点，，
∴，
∵平分，，，
∴，，
∴，
∴；
（2）在和中，，
∴，
∴，
由（1）得，
∴，
∴，
∵，，
∴，
∴，
∴.
23．答案：(1)每个A种纪念章的进价为10元，每个B种纪念章的进价为6元
(2)该专卖店获得销售利润最大的进货方案为购进A纪念章100个，B纪念章300个，最大利润为900元
解析：（1）设每个A种纪念章的进价为x元，则每个B种纪念章的进价为元，
由题意得，，
解得：，
∴，
答：每个A种纪念品的进价为10元，每个B种纪念品的进价为6元；
（2）设购进A种纪念章a个，则购进B种纪念章(400−a)个，利润为w元，
由题意知，，
解得，，
，
∵，
∴w随着a的增大而增大，
∴当时，w最大，值为900，
∴（个），
答：该专卖店获得销售利润最大的进货方案为购进A纪念章100个，B纪念章300个，最大利润为900元.
24．答案：【初步探索】
【探索延伸】仍成立，理由见析
【结论运用】210海里
【灵活变通】，理由见解答过程
解析：【初步探索】如图1，延长到点，使，连接，
在和中，
，
，
，，
∵，
∴，即，
∵，
∴，
在和中，
，
，
，
，
；
【探索延伸】仍成立，理由如下：
如图2，延长到点，使，连接，
，，
，
在和中，
，
，
，，
，，
.
，
，
.
在和中，
，
，
，
，
；
【结论运用】连接，延长、交于点，如图3，
，，
，
，，
在四边形中：，且，
四边形符合探索延伸中的条件，
结论成立，
即（海里），
答：此时两舰艇之间的距离是210海里.
【灵活变通】结论：.
理由：如图4，在延长线上取一点，使得，连接，
，，
，即
在和中，
，
，
，，
∵点在的延长线上，点在的延长线上，仍然满足【初步探索】中的结论，
即，
∴
在和中，
，
，
，
，
，
，
即，
.
进价（元/件）
售价（元/件）
男装
260
320
女装
240
290