专题19 排列组合与二项式定理常考小题（20大核心考点）（讲义）-2024年高考数学二轮复习讲义（新教材新高考）

这是一份专题19 排列组合与二项式定理常考小题（20大核心考点）（讲义）-2024年高考数学二轮复习讲义（新教材新高考），文件包含专题19排列组合与二项式定理常考小题20大核心考点讲义原卷版docx、专题19排列组合与二项式定理常考小题20大核心考点讲义解析版docx等2份试卷配套教学资源，其中试卷共53页， 欢迎下载使用。
一、注意基础知识的整合、巩固。二轮复习要注意回归课本，课本是考试内容的载体，是高考命题的依据。浓缩课本知识，进一步夯实基础，提高解题的准确性和速度
二、查漏补缺，保强攻弱。在二轮复习中，对自己的薄弱环节要加强学习，平衡发展，加强各章节知识之间的横向联系，针对“一模”考试中的问题要很好的解决，根据自己的实际情况作出合理的安排。
三、提高运算能力，规范解答过程。在高考中运算占很大比例，一定要重视运算技巧粗中有细，提高运算准确性和速度，同时，要规范解答过程及书写。
四、强化数学思维，构建知识体系。同学们在听课时注意把重点要放到理解老师对问题思路的分析以及解法的归纳总结，以便于同学们在刷题时做到思路清晰，迅速准确。
五、解题快慢结合，改错反思。审题制定解题方案要慢，不要急于解题，要适当地选择好的方案，一旦方法选定，解题动作要快要自信。
六、重视和加强选择题的训练和研究。对于选择题不但要答案正确，还要优化解题过程，提高速度。灵活运用特值法、排除法、数形结合法、估算法等。
专题19 排列组合与二项式定理常考小题
【目录】
TOC \ "1-3" \h \z \u \l "_Tc157021203" PAGEREF _Tc157021203 \h 2
\l "_Tc157021204" PAGEREF _Tc157021204 \h 3
\l "_Tc157021205" PAGEREF _Tc157021205 \h 3
\l "_Tc157021206" PAGEREF _Tc157021206 \h 5
\l "_Tc157021207" PAGEREF _Tc157021207 \h 6
\l "_Tc157021208" 考点一：二项式定理之特定项、三项式问题 PAGEREF _Tc157021208 \h 6
\l "_Tc157021209" 考点二：二项式定理之系数和问题 PAGEREF _Tc157021209 \h 6
\l "_Tc157021210" 考点三：二项式定理之系数最值问题 PAGEREF _Tc157021210 \h 7
\l "_Tc157021211" 考点四：特殊优先与正难则反策略 PAGEREF _Tc157021211 \h 7
\l "_Tc157021212" 考点五：相邻问题与不相邻问题 PAGEREF _Tc157021212 \h 8
\l "_Tc157021213" 考点六：列举法 PAGEREF _Tc157021213 \h 8
\l "_Tc157021214" 考点七：定序问题（先选后排） PAGEREF _Tc157021214 \h 9
\l "_Tc157021215" 考点八：多面手问题 PAGEREF _Tc157021215 \h 10
\l "_Tc157021216" 考点九：错位排列问题 PAGEREF _Tc157021216 \h 10
\l "_Tc157021217" 考点十：涂色问题 PAGEREF _Tc157021217 \h 10
\l "_Tc157021218" 考点十一：分组与分配问题 PAGEREF _Tc157021218 \h 12
\l "_Tc157021219" 考点十二：隔板法 PAGEREF _Tc157021219 \h 13
\l "_Tc157021220" 考点十三：查字典问题 PAGEREF _Tc157021220 \h 13
\l "_Tc157021221" 考点十四：分解法模型与最短路径问题 PAGEREF _Tc157021221 \h 13
\l "_Tc157021222" 考点十五：构造法模型和递推模型 PAGEREF _Tc157021222 \h 15
\l "_Tc157021223" 考点十六：环排与多排问题 PAGEREF _Tc157021223 \h 16
\l "_Tc157021224" 考点十七：配对型模型 PAGEREF _Tc157021224 \h 16
\l "_Tc157021225" 考点十八：电路图模型 PAGEREF _Tc157021225 \h 17
\l "_Tc157021226" 考点十九：机器人跳动模型 PAGEREF _Tc157021226 \h 17
\l "_Tc157021227" 考点二十：波浪数模型 PAGEREF _Tc157021227 \h 18
排列组合与二项式定理是高考重点考查的内容之一，今后在本节的考查形式依然以选择或者填空为主，以考查基本概念和基本方法为主，难度中等偏下，与教材相当．本节内容与生活实际联系紧密，考生可适当留意常见的排列组合现象，如体育赛事排赛、彩票规则等，培养数学应用的思维意识．

1、如图，在圆中，将圆分等份得到个区域，，，，，现取种颜色对这个区域涂色，要求每相邻的两个区域涂不同的两种颜色，则涂色的方案有种．
2、错位排列公式
3、数字排列问题的解题原则、常用方法及注意事项
（1）解题原则：排列问题的本质是“元素”占“位子”问题，有限制条件的排列问题的限制条件主要表现在某元素不排在某个位子上，或某个位子不排某些元素，解决该类排列问题的方法主要是按“优先”原则，即优先排特殊元素或优先满足特殊位子，若一个位子安排的元素影响到另一个位子的元素个数时，应分类讨论．
4、定位、定元的排列问题，一般都是对某个或某些元素加以限制，被限制的元素通常称为特殊元素，被限制的位置称为特殊位置．这一类问题通常以三种途径考虑：
（1）以元素为主考虑，这时，一般先解决特殊元素的排法问题，即先满足特殊元素，再安排其他元素；
（2）以位置为主考虑，这时，一般先解决特殊位置的排法问题，即先满足特殊位置，再考虑其他位置；
（3）用间接法解题，先不考虑限制条件，计算出排列总数，再减去不符合要求的排列数．
5、解决相邻问题的方法是“捆绑法”，其模型为将n个不同元素排成一排，其中某k个元素排在相邻位置上，求不同排法种数的方法是：先将这k个元素“捆绑在一起”，看成一个整体，当作一个元素同其他元素一起排列，共有种排法；然后再将“捆绑”在一起的元素“内部”进行排列，共有种排法．根据分步乘法计数原理可知，符合条件的排法共有种．
6、解决不相邻问题的方法为“插空法”，其模型为将个不同元素排成一排，其中某个元素互不相邻（），求不同排法种数的方法是：先将（）个元素排成一排，共有种排法；然后把个元素插入个空隙中，共有种排法．根据分步乘法计数原理可知，符合条件的排法共有·种．
7、解决排列、组合综合问题时需注意“四先四后”：
（1）先分类，后分步：某些问题总体不好解决时，常常分成若干类，再由分类加法计数原理解决或分成若干步，再由分步乘法计数原理解决．常常既要分类，又要分步，其原则是先分类，再分步．
（2）先特殊，后一般：解排列、组合问题时，常先考虑特殊情形（特殊元素，特殊位置等），再考虑其他情形．
（3）先分组，后分配：对不同元素且较为复杂的平均分组问题，常常“先分组，再分配”．
（4）先组合，后排列：对于既要选又要排的排列组合综合问题，常常考虑先选再排．
8、求二项展开式中的特定项的方法
求二项展开式中的特定项问题，实质是考查通项的特点，一般需要建立方程求，再将的值代回通项求解，注意的取值范围．
（1）第项：此时，直接代入通项；
（2）常数项：即这项中不含“变元”，令通项中“变元”的幂指数为建立方程；
（3）有理项：令通项中“变元”的幂指数为整数建立方程．
特定项的系数问题及相关参数值的求解等都可依据上述方法求解．
9、赋值法研究二项式的系数和问题
“赋值法”普遍适用于恒等式，是一种重要的方法，对形如，的式子求其展开式的各项系数之和，常用赋值法，只需令即可；对形如的式子求其展开式各项系数之和，只需令即可．
10、二项式系数最大项的确定方法
（1）若是偶数，则中间一项（第项）的二项式系数最大；
（2）若是奇数，则中间两项（第项与第项）的二项式系数相等数最大．
1．（2023•北京）的展开式中，的系数是
A．B．40C．D．80
2．（2023•乙卷）甲乙两位同学从6种课外读物中各自选读2种，则这两人选读的课外读物中恰有1种相同的选法共有
A．30种B．60种C．120种D．240种
3．（2023•新高考Ⅱ）某学校为了了解学生参加体育运动的情况，用比例分配的分层随机抽样方法作抽样调查，拟从初中部和高中部两层共抽取60名学生，已知该校初中部和高中部分别有400名和200名学生，则不同的抽样结果共有
A．种B．种
C．种D．种
4．（2022•新高考Ⅱ）甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演，若甲不站在两端，丙和丁相邻，则不同的排列方式共有
A．12种B．24种C．36种D．48种
5．（2021•乙卷）将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训，每名志愿者只分配到1个项目，每个项目至少分配1名志愿者，则不同的分配方案共有
A．60种B．120种C．240种D．480种
6．（2023•天津）在的展开式中，项的系数为 ．
7．（2022•新高考Ⅰ）的展开式中的系数为 （用数字作答）．
8．（2021•浙江）已知多项式，则 ； ．
9．（2023•新高考Ⅰ）某学校开设了4门体育类选修课和4门艺术类选修课，学生需从这8门课中选修2门或3门课，并且每类选修课至少选修1门，则不同的选课方案共有 种（用数字作答）．
考点一：二项式定理之特定项、三项式问题
【例1】（2024·陕西宝鸡·统考一模）展开式中的第四项为（ ）
A．B．C．240D．
【变式1-1】（2023·上海奉贤·统考一模）若的展开式中存在常数项，则下列选项中的取值不可能是（ ）
A．B．C．D．
【变式1-2】（2024·河南·高三河南省实验中学校考）的展开式中，的系数为（ ）
A．200B．40C．120D．80
【变式1-3】（2024·全国·校联考模拟预测）在的展开式中常数项为（ ）
A．721B．-61C．181D．-59
考点二：二项式定理之系数和问题
【例2】（多选题）（2024·广西·模拟预测）已知，则（ ）
A．展开式中所有二项式的系数和为B．展开式中二项式系数最大项为第1012项
C．D．
【变式2-1】（多选题）（2024·全国·高三专题练习）已知，则（ ）
A．
B．
C．
D．
【变式2-2】（多选题）（2024·河北石家庄·高三河北新乐市第一中学校考阶段练习）若，则下列结论中正确的是（ ）
A．B．
C．D．
【变式2-3】（多选题）（2024·重庆·高三校联考开学考试）已知，则（ ）
A．展开式中二项式系数最大项为第1012项
B．展开式中所有项的系数和为1
C．
D．
考点三：二项式定理之系数最值问题
【例3】（2024·山东日照·高三山东省五莲县第一中学校考）的展开式中第3项与第7项的二项式系数相等，则的展开式中系数最大的项的系数为 .
【变式3-1】（2024·海南海口·海南华侨中学校考一模）在的展开式中，系数最大的项为 .
【变式3-2】（2024·山东青岛·统考三模）若展开式的所有项的二项式系数和为256，则展开式中系数最大的项的二项式系数为 ．（用数字作答）
考点四：特殊优先与正难则反策略
【例4】（2024·浙江·高三慈溪中学校联考）从2位男生，4位女生中安排3人到三个场馆做志愿者，每个场馆各1人，且至少有1位男生入选，则不同安排方法有（ ）种.
A．16B．20C．96D．120
【变式4-1】（2024·甘肃兰州·高二兰州一中校考）4张卡片的正、反面分别写有数字1，2；1，3；4，5；6，7．将这4张卡片排成一排，可构成不同的四位数的个数为（ ）
A．288B．336C．368D．412
【变式4-2】（2024·全国·高三专题练习）将7个人从左到右排成一排，若甲、乙、丙3人中至多有2人相邻，且甲不站在最右端，则不同的站法有（ ）．
A．1860种B．3696种C．3600种D．3648种
【变式4-3】某高中从3名男教师和2名女教师中选出3名教师，派到3个不同的乡村支教，要求这3名教师中男女都有，则不同的选派方案共有（ ）种
A．9B．36C．54D．108
考点五：相邻问题与不相邻问题
【例5】（2024·江苏连云港·高三校考阶段练习）2023年11月12日，连云港市赣马高级中学高品质特色发展暨百年校庆大会隆重举行，赣马高中建校100周年文艺演出中有四个节目：《腰鼓：千年回响》、《歌伴舞：领航》、《器乐：兰亭序》、《情景剧：我们陪你向前走》四个节目，若要对这四个节目进行排序，要求《腰鼓：千年回响》与《歌伴舞：领航》相邻，则不同的排列种数为 （用数字作答）．
【变式5-1】（2024·江西九江·高三校考阶段练习）由1，2，3，4，5，6组成的没有重复数字的六位数，要求奇数1，3，5两两不相邻，但1和2必须相邻，这样的六位数共有 个．
【变式5-2】（2024·全国·高三统考竞赛）某班一天上午有语文、数学、政治、英语、历史5节课，现要安排该班上午的课程表，要求历史课不排在第一节，语文课和数学课相邻，不同的排法总数是 ．
考点六：列举法
【例6】（2024·全国·高三专题练习）某人设计一项单人游戏，规则如下：先将一棋子放在如图所示正方形（边长为2个单位）的顶点处，然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走了几个单位，如果掷出的点数为，则棋子就按逆时针方向行走个单位，一直循环下去.则某人抛掷三次骰子后棋子恰好又回到起点处的所有不同走法共有（ ）
A．21种B．22种C．25种D．27种
【变式6-1】（2024·河北·高三河北衡水中学校考阶段练习）从这100个自然数中随机抽取三个不同的数,这三个数成等差数列的取法数为,随机抽取四个不同的数,这四个数成等差数列的取法数为,则的后两位数字为（ ）
A．89B．51C．49D．13
【变式6-2】（2024·辽宁沈阳·高二东北育才学校校考期末）定义：“各位数字之和为7的四位数叫幸运数”，比如“1006，2023”，则所有“幸运数”的个数为（ ）
A．20B．56C．84D．120
考点七：定序问题（先选后排）
【例7】（2024·全国·高三专题练习）满足，且的有序数组共有（ ）个.
A．B．C．D．
【变式7-1】（2024·高二课时练习）已知，则满足的有序数组共有（ ）个
A．B．C．D．
【变式7-2】（2024·全国·高三专题练习）DNA是形成所有生物体中染色体的一种双股螺旋线分子，由称为碱基的化学成分组成它看上去就像是两条长长的平行螺旋状链，两条链上的碱基之间由氢键相结合．在DNA中只有4种类型的碱基，分别用A、C、G和T表示，DNA中的碱基能够以任意顺序出现两条链之间能形成氢键的碱基或者是A-T，或者是C-G，不会出现其他的联系因此，如果我们知道了两条链中一条链上碱基的顺序，那么我们也就知道了另一条链上碱基的顺序．如图所示为一条DNA单链模型示意图，现在某同学想在碱基T和碱基C之间插入3个碱基A，2个碱基C和1个碱基T，则不同的插入方式的种数为（ ）
A．20B．40C．60D．120
【变式7-3】（2024·全国·高三专题练习）花灯，又名“彩灯”“灯笼”，是中国传统农业时代的文化产物，兼具生活功能与艺术特色.如图，现有悬挂着的8盏不同的花灯需要取下，每次取1盏，则不同取法总数为 （ ）
A．2520B．5040C．7560D．10080
考点八：多面手问题
【例8】（2024·全国·高三专题练习）某龙舟队有9名队员，其中3人只会划左舷，4人只会划右舷，2人既会划左舷又会划右舷．现要选派划左舷的3人、右舷的3人共6人去参加比赛，则不同的选派方法共有（ ）
A．56种B．68种
C．74种D．92种
【变式8-1】（2023·湖北十堰·高二统考期末）某龙舟队有8名队员，其中3人只会划左桨，3人只会划右桨，2人既会划左桨又会划右桨.现要选派划左桨的3人、划右桨的3人共6人去参加比赛，则不同的选派方法共有（ ）
A．26种B．30种C．37种D．42种
【变式8-2】（2024·河南南阳·高三校考阶段练习）我校去年11月份，高二年级有9人参加了赴日本交流访问团，其中3人只会唱歌，2人只会跳舞，其余4人既能唱歌又能跳舞．现要从中选6人上台表演，3人唱歌，3人跳舞，有______种不同的选法
考点九：错位排列问题
【例9】（2024·全国·高三专题练习）编号为1、2、3、4、5的5个人分别去坐编号为1、2、3、4、5的五个座位，其中有且只有两个人的编号与座位号一致的坐法有（ ）
A．10种B．20种C．30种D．60种
【变式9-1】（2024·全国·高三专题练习）将编号为、、、、、的小球放入编号为、、、、、的六个盒子中，每盒放一球，若有且只有两个盒子的编号与放入的小球的编号相同，则不同的放法种数为（ ）
A．B．C．D．
【变式9-2】（2023·吉林延边·高二校考期中）同室4人各写一张贺卡，先集中起来，然后每人从中拿一张别人送出的贺卡，则4张贺卡不同分配方式有
A．8种B．9种C．10种D．12种
考点十：涂色问题
【例10】（2024·江西宜春·高三江西省宜丰中学校考阶段练习）中国是世界上最早发明雨伞的国家，伞是中国劳动人民一个重要的创造．如图所示的雨伞，其伞面被伞骨分成个区域，每个区域分别印有数字，，，，现准备给该伞面的每个区域涂色，要求每个区域涂一种颜色，相邻两个区域所涂颜色不能相同，对称的两个区域如区域与区域所涂颜色相同．若有种不同颜色的颜料可供选择，则不同的涂色方案有
（ ）
A．种B．种
C．种D．种
【变式10-1】（2024·全国·高三专题练习）用6种不同的颜色给如图所示的地图上色，要求相邻两块涂不同的颜色，则不同的涂色方法有（ ）

A．240B．360C．480D．600
【变式10-2】（2024·全国·高三期末）如图是在“赵爽弦图”的基础上创作出的一个“数学风车”平面模型，图中正方形内部为“赵爽弦图”（由四个全等的直角三角形和一个小正方形组成），给、、、这个三角形和“赵爽弦图”涂色，且相邻区域（即图中有公共点的区域）不同色，已知有种不同的颜色可供选择．则不同的涂色方法种数是（ ）

A．B．C．D．
【变式10-3】（2024·广西南宁·南宁二中校考模拟预测）五行是华夏民族创造的哲学思想.多用于哲学、中医学和占卜方面.五行学说是华夏文明重要组成部分.古代先民认为，天下万物皆由五类元素组成，分别是金、木、水、火、土，彼此之间存在相生相克的关系.五行是指木、火、土、金、水五种物质的运动变化.所以，在中国，“五行”有悠久的历史渊源.下图是五行图，现有种颜色可供选择给五“行”涂色，要求五行相生不能用同一种颜色（例如木生火，木与火不能同色，水生木，水与木不能同色），五行相克可以用同一种颜色（例如火与水相克可以用同一种颜色），则不同的涂色方法种数有（ ）

A．B．C．D．
考点十一：分组与分配问题
【例11】（2024·江苏盐城·高三盐城中学校联考阶段练习）将甲，乙，丙，丁，戊五名志愿者安排到四个社区进行暑期社会实践活动，要求每个社区至少安排一名志愿者，那甲恰好被安排在社区的不同安排方法数为（ ）
A．24B．36C．60D．96
【变式11-1】（2024·山西忻州·高三校联考阶段练习）2023年杭州亚运会已圆满落幕，志愿者“小青荷”们让世界看到了新时代中国青年的风采.早在2021年5月，杭州A公司便响应号召，在全公司范围内组织亚运会志愿者的报名与培训，经过选拔，最终有3名党员和3名团员共6人脱颖而出.在彩排环节，需从这6人中选派2人去游泳馆，2人去篮球馆，且要求每个场馆均至少有一位党员，则不同的选派结果有（ ）
A．54种B．45种C．36种D．18种
【变式11-2】（2023·重庆·统考一模）2023年杭州亚运会吉祥物组合为“江南忆”，出自白居易的“江南忆，最忆是杭州”，名为“踪琮”、“莲莲”、“宸宸”的三个吉祥物，是一组承载深厚文化底蕴的机器人为了宣传杭州亚运会，某校决定派5名志愿者将这三个吉祥物安装在学校科技广场，每名志愿者只安装一个吉祥物，且每个吉祥物至少有一名志愿者安装，若志愿者甲只能安装吉祥物“宸宸”，则不同的安装方案种数为（ ）
A．50B．36C．26D．14
考点十二：隔板法
【例12】（2024·湖南长沙·高三湖南师大附中校考阶段练习）将9个志愿者名额全部分配给3个学校，则每校至少一个名额且各校名额互不相同的分配方法总数是（ ）
A．16B．18C．27D．28
【变式12-1】（2024·全国·高三专题练习）7个相同的小球放入，，三个盒子，每个盒子至少放一球，共有（ ）种不同的放法．
A．60种B．36种C．30种D．15种
【变式12-2】（2024·河北衡水·统考模拟预测）将10本完全相同的科普知识书，全部分给甲､乙､丙3人，每人至少得2本，则不同的分法数为（ ）
A．720种B．420种C．120种D．15种
考点十三：查字典问题
【例13】（2024·全国·高二专题练习）用、、、、、六个数字组成无重复数字的四位数，比大的四位数的个数是（ ）
A．B．C．D．
【变式13-1】（2024·北京·高二汇文中学校考）用 四个数字组成无重复数字的四位数， 其中比大的偶数共有（ ）
A． 个B． 个C． 个D． 个
【变式13-2】（2024·山西晋中·高二校考阶段练习）由数字0、1、2、3组成的无重复数字的4位数字中，比2020大的数的个数为（ ）
A．11B．12C．13D．14
考点十四：分解法模型与最短路径问题
【例14】（2024·全国·高三专题练习）有一种走“方格迷宫”游戏，游戏规则是每次水平或竖直走动一个方格，走过的方格不能重复，只要有一个方格不同即为不同走法．现有如图的方格迷宫，图中的实线不能穿过，则从入口走到出口共有多少种不同走法？
A．6B．8C．10D．12
【变式14-1】（2024·全国·高三专题练习）夏老师从家到学校，可以选择走锦绣路、杨高路、张杨路或者浦东大道，由于夏老师不知道杨高路有一段在修路导致第一天上班就迟到了，所以夏老师决定以后要绕开那段维修的路，如图，假设夏老师家在处，学校在处，段正在修路要绕开，则夏老师从家到学校的最短路径有（ ）条．
A．23B．24C．25D．26
【变式14-2】（2024·广东惠州·高三校考期末）如图，某城市的街区由12个全等的矩形组成（实线表示马路），CD段马路由于正在维修，暂时不通，则从A到B的最短路径有（ ）
A．23 条B．24 条C．25条D．26 条
【变式14-3】（2024·全国·高三专题练习）方形是中国古代城市建筑最基本的形态，它体现的是中国文化中以纲常伦理为代表的社会生活规则，中国古代的建筑家善于使用木制品和竹制品制作各种方形建筑.如图，用大小相同的竹棍构造一个大正方体（由个大小相同的小正方体构成），若一只蚂蚁从点出发，沿着竹棍到达点，则蚂蚁选择的不同的最短路径共有（ ）
A．种B．种
C．种D．种
考点十五：构造法模型和递推模型
【例15】（2024·北京海淀·高二北大附中校考期末）几个孩子在一棵枯树上玩耍，他们均不慎失足下落．已知
（）甲在下落的过程中依次撞击到树枝，，；
（）乙在下落的过程中依次撞击到树枝，，；
（）丙在下落的过程中依次撞击到树枝，，；
（）丁在下落的过程中依次撞击到树枝，，；
（）戊在下落的过程中依次撞击到树枝，，．
倒霉的李华在下落的过程中撞到了从到的所有树枝，根据以上信息，在李华下落的过程中，和这根树枝不同的撞击次序有（ ）种．
A．B．C．D．
【变式15-1】（2024·全国·高三专题练习）几只猴子在一棵枯树上玩耍，假设它们均不慎失足下落，已知：（1）甲在下落的过程中依次撞击到树枝A，B，C；（2）乙在下落的过程中依次撞击到树枝D，E，F；（3）丙在下落的过程中依次撞击到树枝G，A，C；（4）丁在下落的过程中依次撞击到树枝B，D，H；（5）戊在下落的过程中依次撞击到树枝I，C，E,则这九棵树枝从高到低不同的顺序共有（ ）
A．23B．24C．32D．33
【变式15-2】（2024·天津河东·高二统考期末）九连环是一种流传于我国民间的传统智力玩具.它用九个圆环相连成串，以解开为胜.它在中国有近两千年的历史，《红楼梦》中有林黛玉巧解九连环的记载.周邦彦也留下关于九连环的名句“纵妙手、能解连环.”九连环有多种玩法，在某种玩法中:已知解下1个圆环最少需要移动圆环1次，解下2个圆环最少需要移动圆环 2 次，记 为解下个圆环需要移动圆环的最少次数，且，则解下 8 个圆环所需要移动圆环的最 少次数为（ ）
A．30B．90C．170D．341
考点十六：环排与多排问题
【例16】（2024·全国·高三专题练习）21个人按照以下规则表演节目：他们围坐成一圈，按顺序从1到3循环报数，报数字“3”的人出来表演节目，并且表演过的人不再参加报数．那么在仅剩两个人没有表演过节目的时候，共报数的次数为（ ）
A．19B．38C．51D．57
【变式16-1】（2024·全国·高三专题练习）A，B，C，D，E，F六人围坐在一张圆桌周围开会，A是会议的中心发言人，必须坐最北面的椅子，B，C二人必须坐相邻的两把椅子，其余三人坐剩余的三把椅子，则不同的座次有（ ）
A．60种B．48种C．30种D．24种
【变式16-2】（2024·全国·高三专题练习）现有一圆桌，周边有标号为1，2，3，4的四个座位，甲、乙、丙、丁四位同学坐在一起探讨一个数学课题，每人只能坐一个座位，甲先选座位，且甲、乙不能相邻，则所有选座方法有（ ）．
A．6种B．8种C．12种D．16种
考点十七：配对型模型
【例17】（2024·浙江·模拟预测）新冠疫情期间，网上购物成为主流．因保管不善，五个快递ABCDE上送货地址模糊不清，但快递小哥记得这五个快递应分别送去甲乙丙丁戊五个地方，全部送错的概率是（ ）
A．B．C．D．
【变式17-1】（2024·黑龙江哈尔滨·高三开学考试）柜子里有3双不同的鞋，随机地取出2只，则取出的鞋一只是左脚的，一只是右脚的，但它们不成对的概率为（ ）
A．B．C．D．
【变式17-2】（2024·重庆·高三重庆一中阶段练习）鞋柜里有4双不同的鞋，从中随机取出一只左脚的，一只右脚的，恰好成双的概率为（ ）
A．B．C．D．
考点十八：电路图模型
【例18】（2024·福建·高二统考期末）如图，电路中共有个电阻与一个电灯A，若灯A不亮，则因电阻断路的可能性的种数为（ ）
A．B．C．D．
【变式18-1】（2024·高二课时练习）如图，电路中共有3个电阻与1个灯泡，若灯泡不亮，则因电阻断路的情况共有 种.
【变式18-2】（2024·高二课时练习）如图所示，在A，B间有四个焊接点，若焊接点脱落，则可能导致电路不通，今发现A，B之间线路不通，则焊接点脱落的不同情况有 种．
考点十九：机器人跳动模型
【例19】（2024·福建龙岩·高二校联考）一只小青蛙位于数轴上的原点处，小青蛙每一次具有只向左或只向右跳动一个单位或者两个单位距离的能力，且每次跳动至少一个单位.若小青蛙经过5次跳动后，停在数考点要求
考题统计
考情分析
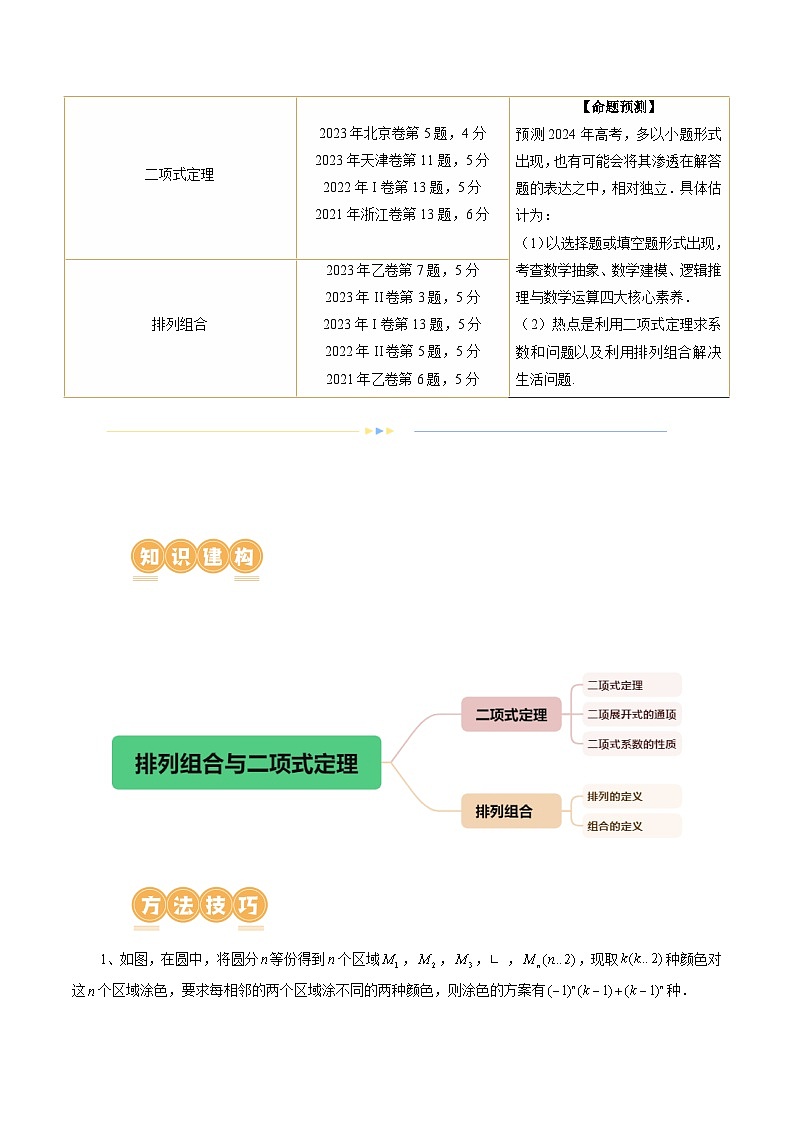
二项式定理
2023年北京卷第5题，4分
2023年天津卷第11题，5分
2022年I卷第13题，5分
2021年浙江卷第13题，6分
【命题预测】
预测2024年高考，多以小题形式出现，也有可能会将其渗透在解答题的表达之中，相对独立．具体估计为：
（1）以选择题或填空题形式出现，考查数学抽象、数学建模、逻辑推理与数学运算四大核心素养．
（2）热点是利用二项式定理求系数和问题以及利用排列组合解决生活问题.
排列组合
2023年乙卷第7题，5分
2023年II卷第3题，5分
2023年I卷第13题，5分
2022年II卷第5题，5分
2021年乙卷第6题，5分